3. Вв порівняння –відношення одного і того ж явища, в різних сукупностях за один і той самий період.

Відносні величини порівняння широко застосовують для оцінки господарської і комерційної діяльності сільськогосподарських підприємств порівняно з показниками району, досягненнями передових господарств однакового виробничого напряму, а також для порівняння показників соціально-економічного розвитку певної країни з відповідними показниками інших країн.

4. ВВ динаміки характеризують зміни однорідних явищу часі.

, (5.11)

В даній величині зпівставляються розміри явищ одного і того ж явища в одній сукупності, але за різні періоди. ВВД є дві, вони взаємопов’язані і доповнюють одна одну. Це Т_р –темп росту, і Т_пр –темп приросту.

(5.12)

, (5.13)

Висновки: В звітному році розмір явища складає …% порівняно з базисним або на …% більше чи менше.

Відносні величини планового завдання, виконання плану і динаміки взаємопов'язані. , (5.14)

Отже, відносна величина динаміки дорівнює добуткові від множення відносних величин планового завдання і виконання плану.

5. Вв структури характеризують частку окремих складових частин у загальному обсязі сукупності.

, (5.15)

Їх виражають найчастіше в процентах. Показники структури обчислюють як відношення частки до цілого. За допомогою показників структури вивчають склад явищ, співвідношення їх складових частин, а також структурні зрушення. Показує яку питому вагу становить частина в загальному обсязі сукупності за тією чи іншою ознакою.

6. Різновидом відносних величин структури є відносні величини координації. Вони показують співвідношення між складовими частинами цілого.

, (5.16)

,

При цьому одну із складових частин цілого беруть за базу порівняння і знаходять відношення решти частин. За базу порівняння береться частина цілого, яка займає найменшу питому вагу.

7. ВВ інтенсивності характеризують відношення двох різнойменних ознак тієї самої сукупності, наприклад співвідношення двох факторів виробництва, або співвідношення факторів і результатів виробництва.

,(5.17)

Показує інтенсивність поширення явища в середовищі.

Тема № 6.Аналіз концентрації, диференціації, та подібності розподілів.

План:

1. Різновиди та характеристики форм розподілів.

2. Оцінка та аналіз нерівномірності розподілів .

3. Оцінка подібності двох розподілів.

1. Різновиди та характеристики форм розподілів.

При вивченні форми розподілу в залежності від значень частот розрізняють одно-, дво- та багатовершинні ряди розподілу. Якісно однорідні сукупності мають одновершинний (одномодальний) розподіл одиниць. Наявність декількох вершин свідчить про неоднорідність сукупності.

Серед одновершинних рядів розподілу розрізняють симетричні та несиметричні, госто- та плосковершинні. У симетричних рядах розподілу середня арифметична, мода і медіана співпадають.

Рис.6.1 Симетричні ряди розподілу.

В асиметричних рядах розподілу вершина зміщена вправо або вліво, а напрямок асиметрії є протилежний до зміщення вершини. Так, при правосторонній асиметрії:

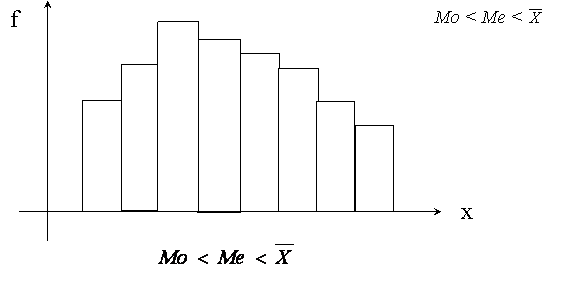
Рис.6.2 Правостороння асиметрія

Рис.6.3 Лівостороння асиметрія

Напрямок та міру асиметрії характеризують коефіцієнти асиметрії, які обчислюються за формулами:

При правосторонній асиметрії А > 0, при лівосторонній А < 0, при симетричному розподілі А = 0. Вважається,

(6.1)

що при |A| < 0,25 асиметрія слабка, при 0,25<|A| <0,5 – середня, при |A| > 0,5 - сильна.

Наприклад, якщо σ = 24,6; X = 180,5; Мо = 164,4; Ме = 170,1 коефіцієнти асиметрії становлять:

Одержані результати свідчать про наявність сильної правосторонньої асиметрії.

Коефіцієнт асиметрії можна також визначити за формулою:

(6.2)

При дослідженні ступеня концентрації одиниць навколо середнього рівня визначають коефіцієнт ексцесу:

(6.3)

При гостровершинному розподілі Е > 0, при плосковершинному Е < 0, а при нормальному розподілі Е = 0. Наприклад:

Отже, в даному випадку має місце слабка плосковершинність розподілу.

Закономірність розподілу одиниць сукупності за значеннями варіючої ознаки можна описати певною функцією, яка має назву теоретичної кривої розподілу. Найбільш часто використовується нормальна крива розподілу, а сам розподіл, котрий можна описати цією кривою, має назву нормального розподілу. Він має наступні властивості:

68,3% одиниць сукупності знаходяться в межах Х ± σ;

95,5% — в межах Х ± 2σ;

99,7% — в межах Х ± 3σ.

Частоти, які розміщені на кривій нормального розподілу, називаються теоретичними частотами (ft). Відхилення теоретичних та фактичних (емпіричних) частот свідчить про ступінь наближення до нормального розподілу.

(6.4)

Теоретичні частоти знаходяться за формулою:

де і - величина інтервалу;

σ - середнє квадратичне відхилення;

уt - ординати кривої нормального розподілу (знаходяться за спеціальними таблицями):

Для об’єктивного судження про відповідність емпіричного розподілу кривій нормального розподілу використовуються спеціальні критерії відповідності (Пірсона, Колмогорова, Ястремського та ін.).

(6.5)

Критерій Пірсона χ2 визначається за формулою:

де f — емпіричні частоти;

ft — теоретичні частоти.

Значення χ2 табульовані для числа ступенів волі k = m–3. У тому випадку, коли χ2 < χ2таб, розподіл можна вважати наближено нормальним, а при χ2 > χ2таб — навпаки, розподіл не можна вважати наближено нормальним.

Отже, χ2 = 6,336. При числі ступенів волі k = 7–3=4 та рівні ймовірності 0,95 χ2таб = 9,5. Оскільки χ2 < χ2таб, розподіл можна вважати наближено нормальним.

(6.6)

Величини χ2 та k використовуються також для розрахунку критерію сполучення Романовського:

Якщо величина Кр менше 3, відмінності між емпіричними та теоретичними частотами можна вважати несуттєвими, а розподіл — наближено нормальним.

У статистичному аналізі часто використовують критерій сполучення Колмогорова (λ):

(6.7)

де |Dmax| — максимальна різниця нагромаджених емпіричних та теоретичних частот.

Із спеціальних таблиць ймовірностей для λ знаходять величину р(λ). Якщо це значення близьке до нуля — розподіл не можна вважати наближено нормальним, якщо р(λ) прямує до 1 — розподіл нормальний.

За раніше наведеним прикладом:

Нагромаджені частоти	fн	2	10	45	86	95	99	100
	fнt	1,47	12,45	44,73	81,17	97,02	99,62	100

Отже, |Dmax| = 4,83. Тоді

З таблиці при λ = 0,483 р(λ) = 0,97.Розподіл можна вважати нормальним.

Аналіз закономірностей розподілу передбачає оцінювання ступеня однорідності сукупності, асиметрії та ексцесу розподілу.

Однорідність сукупності — передумова використання інших статистичних методів (середніх величин, регресійного аналізу тощо). Однорідними вважаються такі сукупності, елементи яких мають спільні властивості і належать до одного типу, класу. При цьому однорідність означає не повну тотожність властивостей елементів, а лише наявність у них спільного в істотному, головному.

В однорідних сукупностях розподіли одновершинні (одномодальні). Багатовершинність свідчить про неоднорідний склад сукупності, про різнотиповість окремих складових. У такому разі необхідно перегрупувати дані, виокремити однорідні групи. Критерієм однорідності сукупності вважається квадратичний коефіцієнт варіації, який завдяки властивостям в симетричному розподілі становить . Згідно з цим критерієм сукупність домогосподарств за рівнем забезпеченості житлом практично однорідна .

З-поміж одновершинних розподілів є симетричні та асиметричні (скошені), гостро- та плосковершинні. У симетричному розподіліасиметричному — вершина розподілу зміщена. Напрям асиметрії протилежний напряму зміщення вершини. Якщо вершина зміщена ліворуч, маємо правосторонню асиметрію, і навпаки. Зазначимо, що асиметрія виникає внаслідок обмеженої варіації в одному напрямі або під впливом домінуючої причини розвитку, яка призводить до зміщення центра розподілу. Ступінь асиметрії різний — від помірного до значного. рівновіддалені від центра значення ознаки мають однакові частоти.

Як уже зазначалося, у симетричному розподілі характеристики центра — середня, мода, медіана — мають однакові значення, в асиметричному між ними існують певні розбіжності. У разі правосторонньої асиметрії , а в разі лівосторонньої, навпаки, . Чим більша асиметрія, тим більше відхилення . Очевидно, найпростішою мірою асиметрії є відносне відхилення , яке характеризує напрям і міру скошеності в середині розподілу; при правосторонній асиметрії .

Теоретично коефіцієнт асиметрії не має меж, проте на практиці його значення не буває надто великим і в помірно скісних розподілах не перевищує одиниці. Так, за даними ряду розподілу (див. табл. 5.4) середній рівень забезпеченості населення житлом становить 9 м2, мода дорівнює 8,1, . Міра скошеності свідчить про помірну правосторонню асиметрію розподілу. Такого самого висновку можна дійти на основі співвідношення середнього квадратичного та середнього лінійного відхилень.

Іншою властивістю одновершинних розподілів є ступінь зосередженості елементів сукупності навколо центра розподілу. Цю властивість називають ексцесом розподілу.

Асиметрія та ексцес — дві пов’язані з варіацією властивості форми розподілу. Комплексне їх оцінювання виконується на базі центральних моментів розподілу. Алгебраїчно центральний момент розподілу — це середня арифметична k-го ступеня відхилення індивідуальних значень ознаки від середньої.

Очевидно, що момент 2-го порядку є дисперсією, яка характеризує варіацію. Моменти 3-го і 4-го порядків характеризують відповідно асиметрію та ексцес. У симетричному розподілі . Чим більша скошеність ряду, тим більше значення . Для того щоб характеристика скошеності не залежала від масштабу вимірювання ознаки, для порівняння ступеня асиметрії різних розподілів використовується стандартизований момент , який на відміну від коефіцієнта скошеності залежить від крайніх значень ознаки. При правосторонній асиметрії коефіцієнт , при лівосторонній . Звідси правостороння асиметрія називається додатною, а лівостороння — від’ємною. Уважається, що при асиметрія низька, якщо не перевищує 0,5 — середня, при — висока.

Для вимірювання ексцесу використовується стандартизований момент 4-го порядку . У симетричному, близькому до нормального розподілі. Очевидно,при гостровершинному розподілі , при плосковершинному .

Аналіз закономірностей розподілу можна поглибити, описати його певною функцією.

Не менш важливими у статистичному аналізі є характеристика нерівномірності розподілу певної ознаки між окремими складовими сукупності, а також оцінка концентрації значень ознаки в окремих її частинах (наприклад, розподіл майна чи доходів між окремими групами населення, кількості зайнятих між окремими галузями промисловості, площі сільськогосподарських угідь між окремими агрогосподарствами).

Так, наведені в табл. 6.1 дані про розподіл промислових підприємств регіону за вартістю основних виробничих фондів і за обсягами спожитої електроенергії свідчать про нерівномірне споживання електроенергії. До першої групи належить 20% підприємств, а частка спожитої електроенергії становить 4%. Натомість шоста група містить 3% підприємств, які споживають 46% електроенергії. На відхиленнях часток двох розподілів — за кількістю елементів сукупності dj і обсягом значень ознаки Dj — ґрунтується оцінювання концентрації.

Таблиця 6.1

ДО РОЗРАХУНКУ КОЕФІЦІЄНТА КОНЦЕНТРАЦІЇ

Вартість основних виробничих фондів, грн.	У % до підсумку		Модуль відхилення часток
	Кількість підприємств dj	Спожито електроенергії Dj
До 5	20	4	0,16
5 — 10	38	5	0,33
10 — 20	22	8	0,14
20 — 50	13	12	0,01
50 — 100	4	25	0,21
100 і більше	3	46	0,43
Разом	100	100	1,28

Якщо розподіл значень ознаки в сукупності рівномірний, то частки однакові — , відхилення часток свідчать про певну концентрацію. Верхня межа суми відхилень , а тому коефіцієнт концентрації обчислюється як півсума модулів відхилень.

Значення коефіцієнта коливаються в межах від нуля (рівномірний розподіл) до одиниці (повна концентрація). Чим більший ступінь концентрації, тим більше значення коефіцієнта K. У нашому прикладі K = 1,28 : 2 = 0,64, що свідчить про високий ступінь концентрації споживання електроенергії у промисловості регіону.

Коефіцієнти концентрації широко використовуються в регіональному аналізі для оцінювання рівномірності територіального розподілу виробничих потужностей, фінансових ресурсів тощо. За кожним регіоном визначається також коефіцієнт локалізації,

який характеризує співвідношення часток.

За даними табл. 6.2 коефіцієнти локалізації свідчать про нерівномірність купівлі (продажу) на душу населення і певною мірою про варіацію життєвого рівня населення різних регіонів.

Таблиця 6.2

КОЕФІЦІЄНТИ ТЕРИТОРІАЛЬНОЇ ЛОКАЛІЗАЦІЇ

Регіон	У % до підсумку		Коефіцієнти локалізації Lj, %
	Чисельність населення dj	Обсяг товарообороту Dj
А	30	34	113
В	50	42	84
С	20	24	120
Разом	100	100	*

Порівняння структур на основі відхилень часток доцільне в рядах з нерівними інтервалами, а надто в атрибутивних рядах.

За аналогією з коефіцієнтом концентрації обчислюється коефіцієнт подібності (схожості) структур двох сукупностей:

Якщо структури однакові, Р = 1; якщо абсолютно протилежні, Р = 0. Чим більше схожі структури, тим більше значення Р. За наведеними у табл. 6.3 даними про галузеву структуру зайнятості населення у двох країнах коефіцієнт подібності структур становить:

тобто розподіл зайнятих за галузями економіки відхиляється в середньому на 18 п. п.

Таблиця 6.3

ГАЛУЗЕВА СТРУКТУРА ЗАЙНЯТОСТІ НАСЕЛЕННЯ

Країна	Структура зайнятих, %
	Сільське господарство	Промисловість та будівництво	Сфера послуг
А	36	24	40
В	25	42	33

Структура будь-якої статистичної сукупності динамічна. Змінюються склад і технічний рівень виробничих фондів, вікова й професійна структура робітників, склад і якість залучених до виробництва природних ресурсів, асортимент і якість продукції, що виробляється, структура споживчого бюджету тощо. Зміна часток окремих складових сукупності свідчить про структурні зрушення. Так, за даними табл. 6.4 структура спожитого в регіоні палива (у перерахунку на умовне) змінилася: зменшились частки газу та мазуту, зросли частки вугілля та інших видів палива. Інтенсивність структурних зрушень оцінюється за допомогою середнього лінійного або середнього квадратичного відхилень часток:

де dj0 та dj1 — частки відповідно базисного та поточного періоду; m — число складових сукупності.

Таблиця 6.4

СТРУКТУРА ТА СТРУКТУРНІ ЗРУШЕННЯ

СПОЖИВАННЯ ПАЛИВА ПО РОКАХ

Вид палива	1995 р., d 0	2000 р., d 1	Відхилення часток, d 1 – d0	Модулі відхилень	Квадрати відхилень,
Вугілля	29	42	13	13	169
Газ	23	16	– 7	7	49
Мазут	45	36	– 9	9	81
Інші види	3	6	+ 3	3	9
Разом	100	100	0	32	308

Лінійний коефіцієнт структурних зрушень становить , тобто частки окремих видів палива змінилися в середньому на 8 п. п. Завдяки своїм математичним властивостям квадратичний коефіцієнт структурних зрушень дещо більший — п. п.

2. Вимірювання й оцінка варіацій та їхні характеристики (абсолютні: варіаційний розмах, середнє лінійне та квадратичне відхилення, дисперсії; відносні: коефіцієнт варіації, нерівномірності, локалізації, концентрації)

Варіаційний розмах характеризує діапазон варіації, це різниця між максимальним і мінімальним значенням ознаки : R=xmax–xmin. Якщо крайні значення ознаки не типові для сукупності, то використовують квартильні або децильні розмахи. Квартильний розмах RQ=Q3–Q1 охоплює 50 % обсягу сукупності, децильний =D8–D2 – 60%, децильний =D9–D1 – 80 %.

Узагальнюючою мірою варіації є середнє відхилення індивідуального значення ознаки від центру розподілу. Позаяк алгебраїчна сума відхилень , то в розрахунках використовують або модулі , або квадрати відхилень. Середній з модулів відхилень називають середнім лінійним відхиленням ; середній квадрат відхилень – дисперсією у2, корінь квадратний з дисперсії – середнім квадратичним відхиленням у:

За первинними, незгрупованими даними наведені характеристики варіації розраховуються за принципом незваженої середньої, тобто:

Середнє лінійне та середнє квадратичне відхилення - іменовані числа (в одиницях вимірювання ознаки) – за змістом ідентичні, проте через математичні властивості у>1. У симетричному, близькому до нормального, розподілі , .

Дисперсію використовують не лише для оцінки варіації, а й при вимірюванні взаємозв’язків, для перевірки статистичних гіпотез тощо. Для ознак метричної шкали розрахунок дисперсії ведеться за формулами

Як і будь-яка середня, дисперсія має певні математичні властивості:

а) якщо всі значення ознаки зменшити (збільшити) на певну величину, дисперсія не зміниться;

б) якщо всі значення ознаки змінити в К разів, то дисперсія зміниться в К2 разів;

в) у разі заміни частот частками дисперсія не зміниться.

Для альтернативної ознаки, варіація якої має два взаємовиключні значення “-1” та “0”, а розподіл характеризується відповідно двома частками –d1 та d0, дисперсія розраховується як добуток часток у2=d1d0 =d1 (1-d1)

Порівнюючи варіації різних ознак або однієї ознаки у різних сукупностях, використовують відносні характеристики варіації. Коефіцієнти варіації розраховуються як відношення абсолютних, іменованих характеристик варіації до центру розподілу і часто виражається процентами, отже:

1) лінійний коефіцієнт варіації;

2) квадратичний коефіцієнт варіації;

3) коефіцієнт осциляції.

Якщо центр розподілу представлений медіаною, то використовують квартильний коефіцієнт варіації:. Мірою оцінки розшарування сукупності слугує також коефіцієнт децильної диференціації . У ряду розподілу держоблігацій за терміном обертання ,.

Найпростішою мірою асиметричності розподілу є відхилення між характеристиками центру розподілу. Позаяк у симетричному розподілі , то чим помітніша асиметрія, тим більше відхилення . Стандартне відхилення називають коефіцієнтом асиметрії .

Оцінка нерівномірності розподілу значень ознаки між окремими складовими сукупності грунтується на порівнянні часток двох розподілів – за кількістю елементів сукупності dj та за обсягом значень ознаки Dj . Відхилення часток свідчить про певну нерівномірність розподілу, яка вимірю

локалізації концентрації .

Коефіцієнт локалізації розраховується для кожної j-ї складової сукупності. За рівномірного розподілу всі значення Lj=1. У випадку концентрації значень ознаки в j-ій складовій Lj?1, і навпаки.

Коефіцієнт концентрації є узагальнюючою характеристикою відхилення розподілу від рівномірного. Значення його коливаються у межах від 0 до 1. У рівномірному розподілі К=0. Чим помітніша концентрація, тим більше значення К відхиляється від 0.

Коефіцієнти концентрації та локалізації є ефективним засобом вимірювання диференціації сукупності за даними інтервальних рядів з нерівними інтервалами та за даними атрибутивних рядів. За аналогією з коефіцієнтом концентрації розраховують коефіцієнт подібності (схожості) структур двох об’єктів або одного об’єкта за двома ознаками.

Якщо структури однакові, Р=1. Чим більші відхилення структур, тим менше значення коефіцієнта Р.

Для оцінки інтенсивності структурних зрушень у часі використовують абсолютні міри варіації – середнє лінійне або середнє квадратичне відхилення часток, які називають коефіцієнтами структурних зрушень.

лінійний квадратичний

де dj0 та dj1 – частки розподілу за два періоди; m –число складових сукупності.