
- •Раздел 1 – Линейная алгебра.
- •Найти значение матричного многочлена, если , если
- •Раздел 2 – Векторная алгебра.
- •Модуль 2 Раздел 3 – Аналитическая геометрия на плоскости и в пространстве. Прямая на плоскости
- •Кривые 2 порядка.
- •Плоскость и прямая в пространстве.
- •Поверхности 2 порядка.
- •Модуль 3 Раздел 3 – Абстрактная алгебра.
- •Раздел 4 – Комплексные числа.
- •Найти , если .
- •Дано: , .
Банк задач для подготовки к экзамену
ГРФ
Дисциплина математика
I семестр 2013-2014
Модуль 1
Раздел 1 – Линейная алгебра.
Решить уравнение
 .
.Вычислить определитель
 .
.Найти
 ,
если
,
если
 ,
,
 .
.Дано
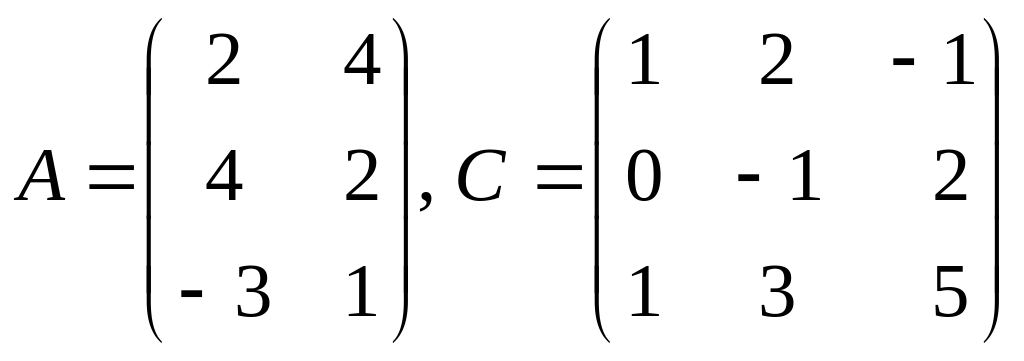 .
.
Существует ли CА и АC? Если да, найдите их.
Найти решение системы
 методом Крамера
методом Крамера
 .
В ответе указать
.
В ответе указать

Решить систему матричным методом и методом Крамера
 .
.Решить систему методом Гаусса
 .
.Найти фундаментальную систему решений
![]()
Найти ранг, норму, след, собственные числа и собственные векторы матрицы

Найти ранг, норму, след, число обусловленности , собственные числа и собственные векторы матрицы
 .
.
Решить матричное уравнение:

Найти значение матричного многочлена, если
 , если
, если
 .
.Найти значение матричного многочлена, если , если
 .
.
Раздел 2 – Векторная алгебра.
Определить начало вектора
 ,
если его конец совпадает с точкой
(1;-1;2), найти соответствующий ему
нормированный вектор.
,
если его конец совпадает с точкой
(1;-1;2), найти соответствующий ему
нормированный вектор.
Векторы
 и
и
 образуют
угол
образуют
угол
 ,
причем
,
причем
 .
Определить
.
Определить
 и
и
 .
.
При каких
 скалярное произведение векторов
скалярное произведение векторов
 и
и
 равно 0.
равно 0.При каких
 векторное произведение векторов
и
векторное произведение векторов
и
 равно 0.
равно 0.Коллинеарны ли векторы
 и
и
 ,построенные
по векторам
,построенные
по векторам
 и
и
 ?
?
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Найти косинус угла между векторами
 и
и
 .
.
![]() ,
,
![]() ,
,
![]() .
.
Вычислить площадь параллелограмма, построенного на векторах и .
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Компланарны ли векторы , и
 ?
?
![]() .
.
Вычислить объем тетраэдра с вершинами в точках
 и
его высоту, опущенную из вершины
и
его высоту, опущенную из вершины
 на грань
на грань
 .
.
![]() .
.
Проверить, что 4 точки A(3;-1;2), B(1,2,-1), C(-1,1,-3), D(3;-5;3) служат вершинами трапеции.
Даны вершины
 :
A(-1;-2;4), B(-4,-2,0),
C(3,-2,1). Определить его
внутренний угол при вершине B.
:
A(-1;-2;4), B(-4,-2,0),
C(3,-2,1). Определить его
внутренний угол при вершине B.Даны вершины : A(1;-1;2), B(5,-6,2), C(1,3,-1). Вычислить длину его высоты, опущенной из вершины B на сторону AC.
Даны 3 вектора
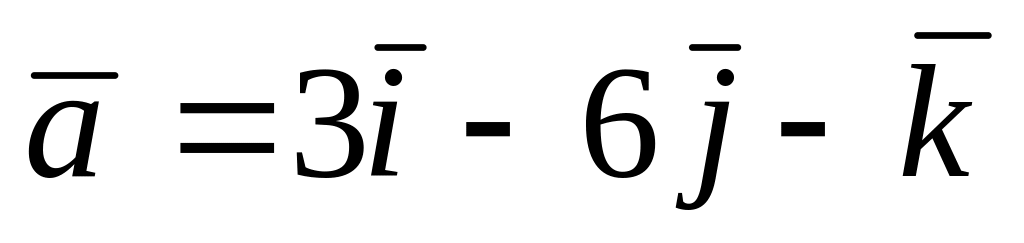 ,
,
 ,
,
 .
Найти: 1)
.
Найти: 1)
 ;
2)
;
2)
 .
.Установить, компланарны ли векторы


 .
Если векторы компланарны, найти линейную
зависимость между ними.
.
Если векторы компланарны, найти линейную
зависимость между ними.Разложить вектор
 по трем некомпланарным векторам
по трем некомпланарным векторам
 ,
,
 ,
,
 .
.Написать разложение вектора
 по векторам
по векторам
 ,
предварительно доказав что они образуют
базис.
,
предварительно доказав что они образуют
базис.
![]()
Найти координаты вектора
 в новом базисе
в новом базисе
 ,
,
 ,
,
 .
.
Модуль 2 Раздел 3 – Аналитическая геометрия на плоскости и в пространстве. Прямая на плоскости
Найти координаты точки, делящей отрезок АВ в отношении 3:4 от начала. Координаты точек А(1;6), В(-3;8).
Составить уравнение прямой, проходящей через точку K(2;2) параллельно прямой
 .
.Написать уравнение прямой, проходящей через точки E(1;3) и F(5;2). Найти точки пересечения данной прямой с осями координат.
Даны вершины треугольника: A(4;1), B(0;-2), C(-5;10).
Найти: 1) Уравнение стороны BC; 2) Длину стороны BC; 3) Уравнение высоты, проведенной из вершины A; 4) Длину высоты, проведенной из вершины A; 5) Уравнение медианы, проведенной из вершины В; 6) Уравнение средней линии, параллельной стороне ВС; 7) площадь треугольника АВС; 8) Угол B; 9) Сделать чертеж.
Даны координаты вершин треугольника АВС: А(4;5), В(1;1), С(-5;9). Найти уравнение высоты АД; уравнение средней линии треугольника КМ, параллельной стороне АВ; угол между АД и КМ.
Даны уравнения двух сторон параллелограмма: x-y-1=0 и x-2y-1=0 и точка P(2;2) пересечения его диагоналей. Составить уравнения двух других сторон параллелограмма. Сделать чертеж.
Найдите координаты вершин треугольника, стороны которого лежат на прямых, заданных уравнениями
 ,
,
 ,
,
 .
.
