Вариант № 19
Найти общее решение (общий интеграл) дифференциального уравнения:
а)
; b)
;
c)
.
Найти частное решение (частный интеграл) дифференциального уравнения:
.
Найти общее решение дифференциального уравнения:
.
Найти частное решение дифференциального уравнения и вычислить значение полученной функции при с точностью до двух знаков после запятой.
.
Найти общее решение дифференциального уравнения, допускающего понижение порядка:
.
Решить задачу Коши для дифференциального уравнения, допускающего понижение порядка:
.
Проинтегрировать следующее уравнение:
.
Записать уравнение кривой, проходящей через точку А(4, -3) и обладающей следующим свойством: длина перпендикуляра, опущенного из начала координат на касательную к кривой, равна абсциссе точки касания.
Найти общее решение ЛОДУ второго порядка.
1.
2.
3.
Найти частное решение ДУ
Определить и записать структуру частного решения ЛНДУ по виду функции f(x):
Найти частное решение :
Найти общее решение ЛНДУ
;
Найти общее решение ЛНДУ методом вариации постоянных
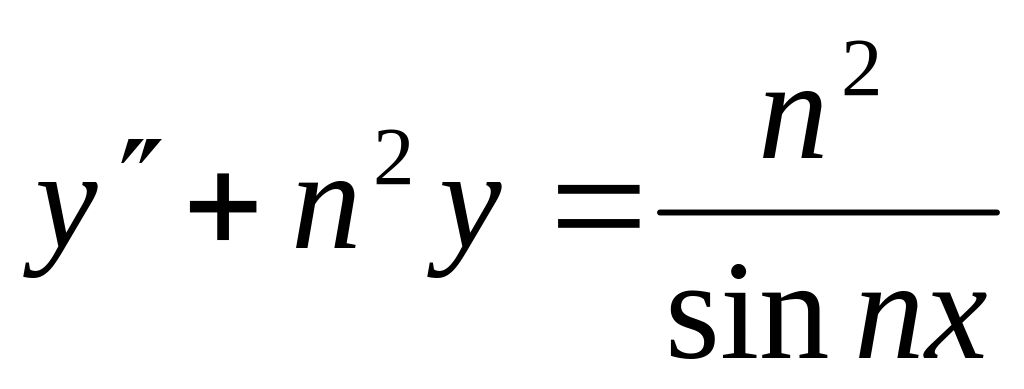.Решить систему дифференциальных уравнений
ТИПОВОЙ РАСЧЕТ
по теме “Дифференциальные уравнения”
Вариант № 20
Найти общее решение (общий интеграл) дифференциального уравнения:
а)
;
b)
; c)
.
Найти частное решение (частный интеграл) дифференциального уравнения:
.
Найти общее решение дифференциального уравнения:
.
Найти частное решение дифференциального уравнения и вычислить значение полученной функции при с точностью до двух знаков после запятой.
.
Найти общее решение дифференциального уравнения, допускающего понижение порядка:
.
Решить задачу Коши для дифференциального уравнения, допускающего понижение порядка:
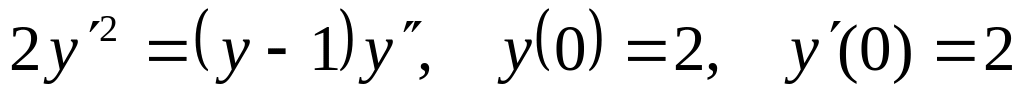.Проинтегрировать следующее уравнение:
.
Записать уравнение кривой, проходящей через точку А(5, 0) и обладающей следующим свойством: длина перпендикуляра, опущенного из начала координат на касательную к кривой, равна абсциссе точки касания.
Найти общее решение ЛОДУ второго порядка.
1.
2.
3.
Найти частное решение ДУ :
Определить и записать структуру частного решения ЛНДУ по виду функции f(x):
Найти частное решение ЛНДУ:
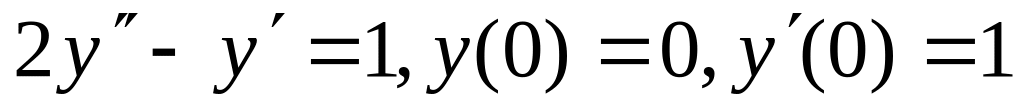
Найти общее решение ЛНДУ
;
Найти общее решение ЛНДУ методом вариации постоянных
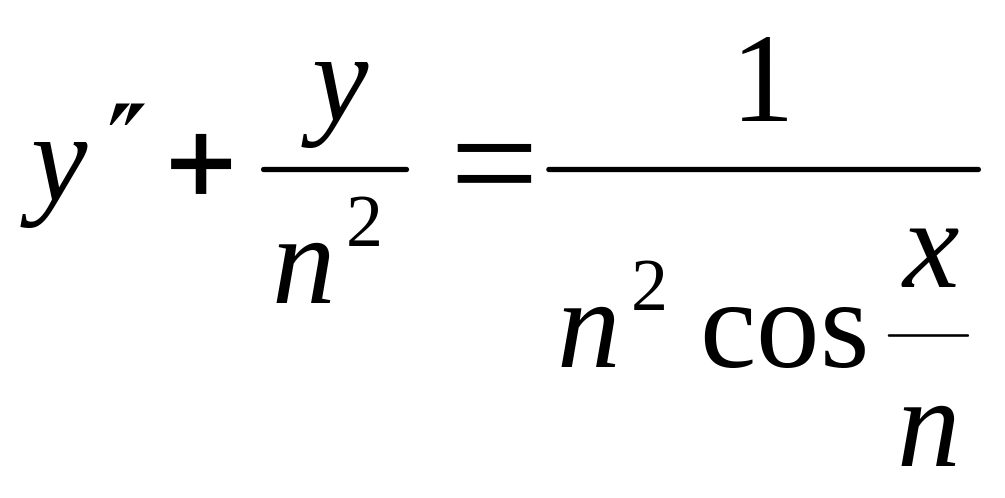.Решить систему дифференциальных уравнений
ТИПОВОЙ РАСЧЕТ
по теме “Дифференциальные уравнения”
Вариант № 21
Найти общее решение (общий интеграл) дифференциального уравнения:
а)
;
b)
;
c)
.
Найти частное решение (частный интеграл) дифференциального уравнения:
.
Найти общее решение дифференциального уравнения:
.
Найти частное решение дифференциального уравнения и вычислить значение полученной функции при с точностью до двух знаков после запятой.
.
Найти общее решение дифференциального уравнения, допускающего понижение порядка:
.
Решить задачу Коши для дифференциального уравнения, допускающего понижение порядка:
.
Проинтегрировать следующее уравнение:
.
Записать уравнение кривой, проходящей через точку А(4, 1) и обладающей следующим свойством: отрезок, который касательная в любой точке кривой отсекает на оси ОУ, равен квадрату абсциссы точки касания.
Найти общее решение ЛОДУ второго порядка.
1.
2.
3.
Найти частное решение ДУ
Определить и записать структуру частного решения ЛНДУ по виду функции f(x):
Найти частное решение
Найти общее решение ЛНДУ
;
Найти общее решение ЛНДУ методом вариации постоянных
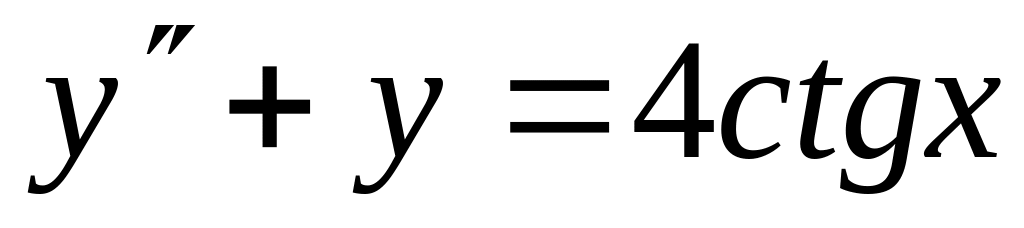.Решить систему дифференциальных уравнений
ТИПОВОЙ РАСЧЕТ
по теме “Дифференциальные уравнения”