Задачи 21-30

• Для заданного ступенчатого бруса построить эпюры продольных сил и нормальных напряжений.

При работе бруса на растяжение и сжатие в его поперечных сечениях возникает продольная сила N. Продольная сила в произвольном поперечном сечении бруса численно равна алгебраической сумме проекций на его продольную ось всех внешних сил, действующих на отсечённую часть N = Σ F_i.

Для расчёта на прочность и определение перемещений необходимо знать закон изменения продольных сил по его длине. Правило знаков: при растяжении продольная сила положительна, при сжатии - отрицательна. Условие прочности при растяжении и сжатии имеет вид

=

где σ, N - соответственно нормальное напряжение и продольная сила в опасном сечении (т. е. в сечении, где возникают наибольшие напряжения), А - площадь поперечного сечения, [σ] - допускаемое напряжение.

Дано: Е = 2·10⁵ МПа,

F₁ = 30кН, F₂ = 38кН,

F₃ = 42кН, А₁ = 1,9см²,

А₂ = 3,1см².

Определить: перемещение Δℓ свободного конца бруса. Проверить прочность бруса и указать, насколько (в процентах) брус недогружен или перегружен, если [Ϭ] = 160 МПа.

Решение:

1. Со свободного конца разбиваем брус на участки. Определяем ординаты эпюры N на участках бруса

N_I = 0;

N_II = F₁ = 30кН;

N_III = F₁ = 30кН;

N_IV = F₁-F₂ = 30-38 = -8кН;

N_V = F₁ – F₂ – F₃ = 30-38-42 = -50кН.

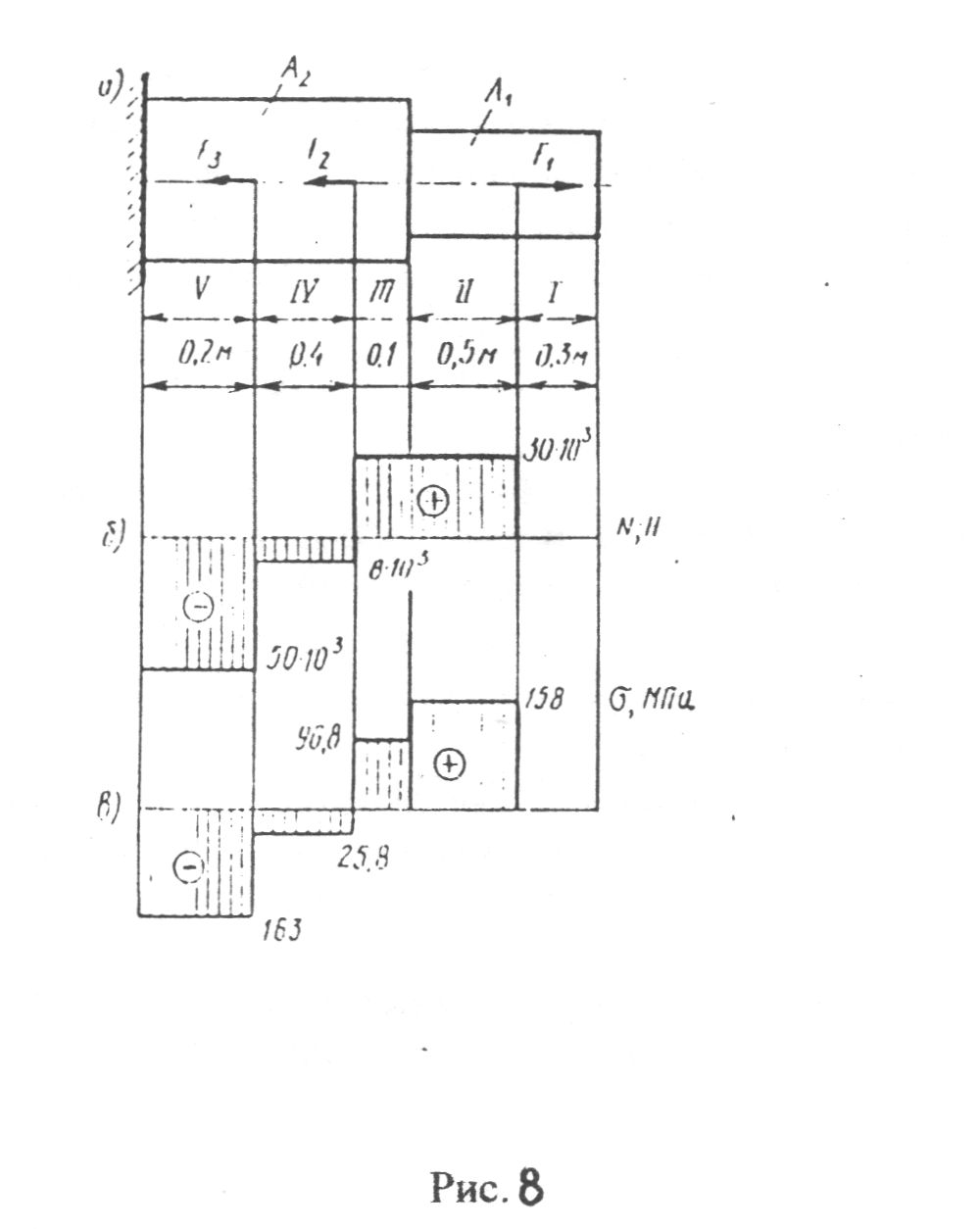
Строим эпюру продольных сил.

2. Определяем ординаты эпюр нормальных напряжений:

Ϭ_I = = 0;

Ϭ_II = = = 158 МПа;

Ϭ_III = = 96,8 МПа;

Ϭ_IV = =

Ϭ_V = = = -161,3 МПа.

Строим эпюру нормальных напряжений.

3. Определяем перемещение свободного конца бруса:

Δℓ = Δℓ₁ + Δℓ₂ + Δℓ₃ + Δℓ₄ + Δℓ₅

Δℓ₁ = = 0;

Δℓ₂ = =

Δℓ₃ = =

Δℓ₄ = = -

Δℓ₅ = =

Δℓ =

4. Определяем процент перегрузки:

ΔϬ =

Ответ: Δℓ = 0,81%.

Задачи 31-40

• Для заданного стального бруса определить значения моментов М_АВ, М_ВС, М_СД; построить эпюры крутящих моментов.

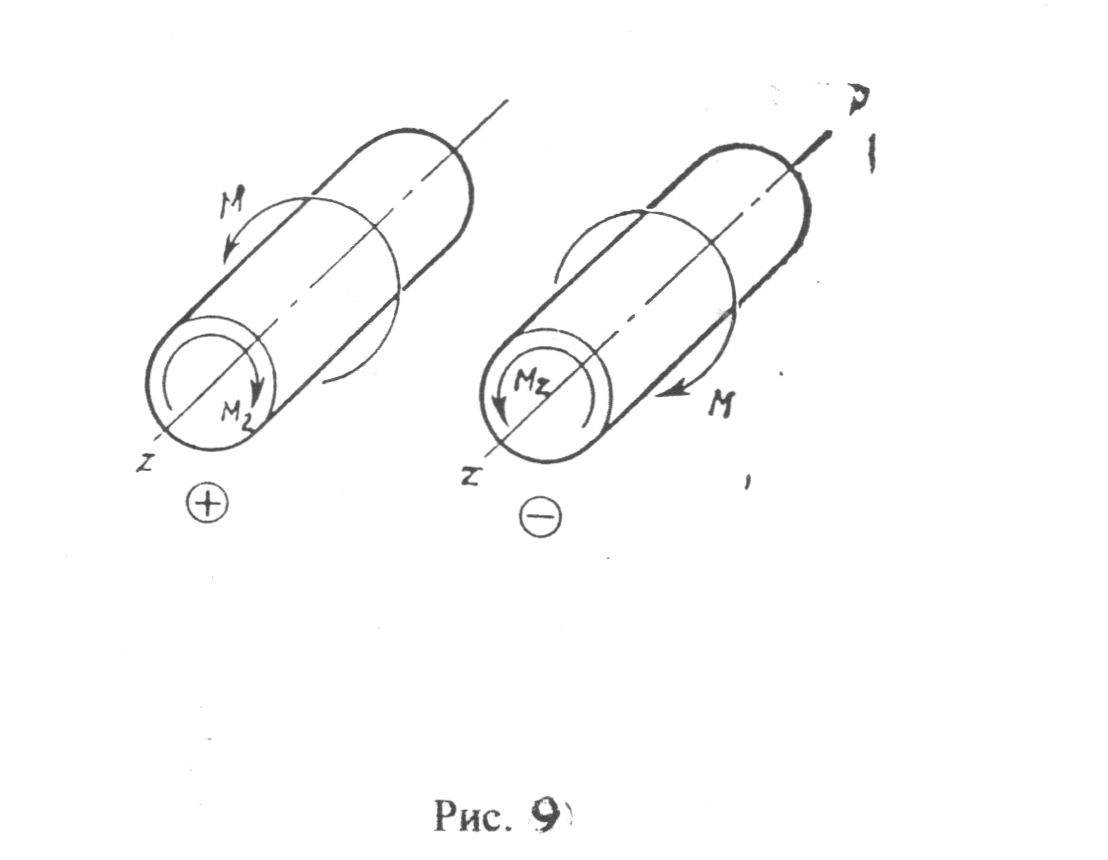Кручением называют такой вид нагружения бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент М_кр (М_z). Крутящий момент в произвольном поперечном сечении бруса равен алгебраической сумме внешних моментов, действующих по одну сторону от сечения

Имеется в виду, что плоскости действия всех внешних моментов М_кр перпендикулярны продольной оси бруса.

Будем считать крутящий момент положительным, если для наблюдателя, смотрящего на проведенное сечение, он представляется проведенным по часовой стрелке. Соответствующий внешний момент направлен против часовой стрелки.

Дано:

Р₁ = 9 кВт;

Р₂ = 15 кВт;

Р₃ =3 кВт;

ω = 10 .

Решение:

1. Определяем значения моментов М_АВ, М_ВС, М_СД:

М _АВ = = 900 Нм;

М _ВС = = = 1500 Нм;

М _СД = = = 300 Нм.

2. Строим эпюру крутящих моментов, применяя метод сечения. Проводя мысленно сечение в пределах каждого из участков, идя от свободного конца,

будем отбрасывать закрепленную часть бруса и оставлять для рассмотрения незакрепленную:

М_{кр АВ} = М_АВ = 900 Нм;

М_{кр ВС} = М_АВ+М_ВС = -900 + 1500 = 600 Нм;

М_{кр СД} = М_АВ+М_ВС+М_СД = -900+1500-300 = 300 Нм.

Ответ: М_{кр АВ} = 900 Нм; М_{кр ВС} = 600 Нм; М_{кр СД} = 300 Нм.