Урок №3 (8 клас)

Тема уроку: Застосування подібності трикутників для розв'язування задач.

Цілі уроку:

• дидактична - узагальнити поняття «подібні трикутники», повторити ознаки подібності трикутників, навчити використовувати цей матеріал під час розв’язування задач;

• розвивальна - стимулювати самостійне узагальнення матеріалу, сприяти розвитку алгоритмічного мислення, розвивати в учнів конструктивний підхід до розв'язування задач;

• виховна - виховувати інтерес до предмету через створення ситуацій успіху, сприяти вихованню взаємодопомоги під час колективної роботи, графічної грамотності.

Тип уроку: узагальнення й систематизація знань.

Способи організації навчально-пізнавальної діяльності учнів: фронтальна, індивідуальна, колективна.

Основні методи навчання: метод вправ, метод збудження інтересу, розв'язування усних та письмових вправ.

Наочність та обладнання: карточки із самостійною роботою, підручник, креслярські інструменти.

Основна література: 1) Бевз Г.П. Геометрія: Підручник для 8 кл. загальноосвітн. навч. закладів. – К.: Вежа, 2007. – 256 с.: іл.; 2) Бурда М.І. Геометрія: Підручник для 8 класу загальноосвітн. навч. закладів. – К.: Зодіак – ЕКО, 2008. – 240 с.; 3) Шарапа Валентина. Конструктивні задачі в 8 класі // Математика в школах України. – 2003. - №1 (13). - С. 16-17.

Очікувані результати навчання: учні повинні

знати визначення подібних трикутників, ознаки подібності, властивість бісектриси кута трикутника, суть методів алгебраїчних та геометричних перетворень (методу подібності);

мати уявлення про геометричні побудови на площині;

вміти застосовувати знання про подібні трикутники при розв'язування задач, а також методів алгебраїчних та геометричних перетворень при розв’язуванні конструктивних задач.

План уроку

I. Перевірка домашнього завдання (5 хв.)

II. Закріплення засвоєних навичок та вмінь учнів (33 хв.)

III. Підсумки уроку (5 хв.)

IV. Домашнє завдання (2 хв.)

Хід уроку

I. Опитування учнів. Викликаний до дошки учень розбирає розв’язання задачі за готовим рисунком.

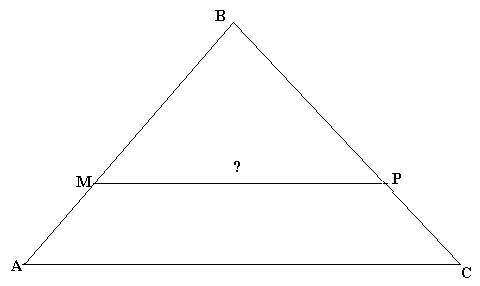Дано: АВС,

МР || АС, АС=16,

СВ=8, PB=5.

Знайти: MP

Виберіть правильні твердження:

А) Б)

В)

II. Розв'язування задач

З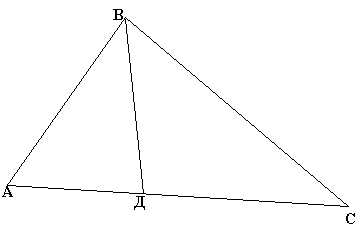 адача 1. В трикутнику із сторонами 3, 5 та 7 см проведена бісектриса найбільшого кута. Знайдіть довжини відрізків, на які розбиває протилежну сторону бісектриса.

Слід згадати: 1) який з кутів в трикутнику вважається найбільшим? Найменшим? Чому? 2) властивість бісектриси кута трикутника.

За умовою АВ=3 см, ВС=5 см, АС=7 см. Оскільки АС – найдовша сторона, то кут, що лежить навпроти неї, повинен бути найбільшим. Тому кут В – найбільший. Отже, проведено бісектрису ВД.

За властивістю бісектриси кута трикутника, знаходимо АД, позначивши її перед цим через х:

Звідси:

Оскільки АС=АД+ДС, то ДС= .

Задача 2. Дано рівносторонній трикутник АВС. Побудувати відрізок КР, перпендикулярний до АС, так, щоб один кінець, точка К, лежав на стороні АВ і виконувалась рівність ВК=АР.

Р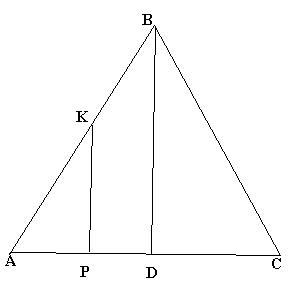 озв’язання

Припустимо, що відрізок КР побудовано. Позначимо сторону трикутника АВС через а і опустимо з вершини В перпендикуляр на АС. Для побудови відрізка КР потрібно встановити положення точок К і Р на сторонах АВ і АС. Ці точки задовольняють умови: лежать відповідно на відрізках АС і АВ та на колах з центром у точці А радіусом АР із центром в точці В і радіусом ВК. Відрізки АР і ВК невідомі. Позначимо їх через , тоді АР=ВК= . Оскільки КР || ВD, то  , і тоді (1)

Враховуючи позначення, рівність (1) перепишемо так:

, або . Звідси . Положення точок К і Р – відоме.

Побудова: будуємо відрізок , відрізки на сторонах АВ і АС від точок В і А, відрізок КР. Відрізок КР – шуканий.

Самостійна робота (слід роздати учням карточки із завданням самостійної роботи одного варіанту).

1. Три сторони одного трикутника пропорційні тьом сторонам другого трикутника. Знайти сторони другого трикутника, якщо його периметр дорівнює 72 см, а сторони першого – 4 см, 6 см і 8 см.

2. Побудувати прямокутний трикутник, подібний даному, так, щоб висота, проведена з вершини прямого кута, дорівнювала відрізку .

III. Запитання до класу:

• які трикутники є подібними;

• скільки існує ознак подібності трикутників;

• назвіть їх;

• яку властивість має бісектриса кута трикутника.

IV. Домашнє завдання (з коментарями)

Бурда М.І.: параграф 14, №612 (4) + задача.

Задача: Знайти поза даним колом таку точку, щоб дотична, проведена з неї до цього кола, була вдвічі меншою від січної, проведеної з тієї самої точки через центр.

Задачу слід розв’язати алгебраїчним методом. Звернути увагу на те, що відстань шуканої точки від центра кола позначити через х. Тоді довжина січної , а довжина дотичної .