Урок №1 (7 клас)
Тема: Метод геометричних місць
Цілі уроку:
• дидактична - домогтися засвоєння учнями схеми дій, що покладені в основу методу ГМТ при розв’язуванні задач на побудову;
• розвивальна - сприяти розвитку алгоритмічного мислення, просторової уяви, пам'яті, уваги, загальнонавчальних вмінь: аналізувати, синтезувати, узагальнювати;
• виховна - сприяти вихованню взаємодопомоги під час організації роботи в групах, графічної грамотності.
Тип уроку: засвоєння знань, умінь та навичок.
Способи організації навчально-пізнавальної діяльності учнів: групова, індивідуальна, фронтальна бесіда.
Основні методи навчання: конкретно-індуктивний, наочні методи, самостійна робота, розв'язування усних та письмових вправ.
Наочність та обладнання: набір демонстраційного креслярського приладдя, підручник.
Основна література: 1) Бевз Г.П. Геометрія: Підручник для 7 кл. загальноосвітн. навч. закладів. – К.: Вежа, 2007. – 208 с.: іл.; 2) Бабенко С.П. Уроки геометрії. 7 клас / С.П. Бабенко. – Х.: Вид. група «Основа», 2007. – 208 с.
Очікувані результати навчання: учні повинні
знати визначення поняття геометричного місця точок, суть методу ГМТ, алгоритм його здійснення;
мати уявлення про основні задачі на побудову, які розв’язуються за допомогою методу ГМТ;
вміти використовувати метод ГМТ при розв’язуванні задач на побудову (відтворювати схему, що лежить в основі методу геометричних місць).
План уроку
Перевірка домашнього завдання ( 10 хв.)
Мотивація навчальної діяльності. Формування мети й завдань уроку ( 8 хв.)
Засвоєння нових знань (5 хв.)
Первинне усвідомлення нового матеріалу (15 хв.)
Підсумки уроку (3 хв.)
Домашнє завдання ( 4 хв.)
Хід уроку
I. Виконання усних вправ перевіряємо під час фронтальної бесіди (Що називається ГМТ? Як провести через дану точку О пряму, перпендикулярну даній прямій а? Скільки можливо випадків?), письмових вправ – за допомогою самоперевірки (розв'язування задачі вчитель заготовив на дошці).
II. Для мотивації пропонуємо учням виконати завдання:
знайдіть ГМТ, рівновіддалених від точок А і В;
знайдіть ГМТ, віддалених від точок А і В на певну відстань а;
знайдіть ГМТ, рівновіддалених від точок А, В, С (точки А, В, С не лежать на одній прямій).
Порівняння умов запропонованих завдань приводить до формулювання проблеми, яку треба розв’язати: як побудувати геометричне місце точок, які задовольняють одночасно дві (а не одну) умови?
Пошук відповіді на це питання і є основною дидактичною метою уроку.
III. Міркування, що лежать в основі методу геометричних місць є досить простими і зрозумілими учням. Викладення цих міркувань учитель може проводити індуктивним або дедуктивним методом, тобто на прикладі однієї із запропонованих на третьому етапі задач продемонструвати хід міркувань, а потім узагальнити ці міркування або навпаки – сформулювавши загальні твердження, потім розглянути приклади його застосування.
IV. Виконання письмових вправ.
В умовах наступних задач усно виділити дві умови, які повинні задовольняти шукане ГМТ.
1. Точки А, В, С не лежать на одній прямій. Побудуйте точку, рівновіддалену від точок А, В, С.
Дано точки А, В, С. Побудуйте точку, яка рівновіддалена від точок А і В і лежить на заданій відстані від точки С.
Побудуйте точку, рівновіддалену від сторін даного кута, яка лежить на відстані d від його вершини.
Точка А лежить на колі радіуса R. Побудуйте точки даного кола, віддалені від точки А на відстань R.
Після виконання такого аналізу умов задач, починаємо письмове розв’язання задач №1 і №3.
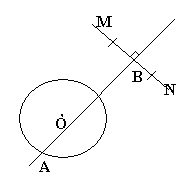
V. Питання для бесіди: що сьогодні нового ви дізналися? З якими ГМТ познайомилися? Які для цього ми використовували методи?
А тепер за рисунком сформулюйте задачу, розв’язком якої є точки А і В.
VI.Домашнє завдання (з коментарями)
Розв’язати задачі №2, 3 класної роботи. Задачу під №3 слід розв’язати наступним чином:
провести серединний перпендикуляр до відрізка AB;
провести серединний перпендикуляр до відрізка BC;
знайти точку перетину цих серединних перпендикулярів і зробити висновки щодо шуканого ГМТ.
Розв’язати методом геометричних місць задачу: знайдіть геометричне місце центрів кіл радіуса R, що проходить через дану точку А.