Метод паралельного перенесення
Під час розв'язування деяких задач часто виникають труднощі при побудові шуканої фігури тільки через те, що частини цієї фігури дуже віддалені одна від одної, і тому важко ввести в малюнок дані елементи. Такими, наприклад, є задачі на побудову многокутників (які не є трикутниками), де зближення даних і шуканих елементів дає можливість звести задачу до побудови деякого трикутника, в якого відомі три елементи. Зближення елементів фігур зручно здійснювати методом паралельного перенесення.
У 9 класі при вивченні теми «Паралельне перенесення» розв’язуємо задачі на побудову методом паралельного перенесення.
Спочатку повторюємо з курсу 8 класу розв'язування задачі на побудову трапеції за основами і бічними сторонами. На прикладі цієї задачі пояснюємо суть методу паралельного перенесення: при аналізі задачі яку-небудь частину фігури паралельно переносять на деяку відстань у певному напрямі, завдяки чому дістають допоміжну фігуру, яку легко побудувати. Побудувавши допоміжну фігуру, виконують паралельне перенесення в протилежному напрямі на таку саму відстань. Дістають шукану фігуру.
Алгебраїчний метод
Суть методу полягає в тому, що проводячи аналіз задачі на побудову, положення на площині шуканого елемента знаходимо за допомогою алгебри. Припустивши, що задачу розв’язано, виділяємо на малюнку-ескізі шуканий елемент, до визначення якого зводиться розв'язування задачі. На підставі умови задачі і геометричних теорем складаємо рівняння, розв’язуючи яке знаходимо для шуканого елемента алгебраїчний вираз. Побудувавши його за допомогою креслярських інструментів, знаходимо положення шуканого елемента, а отже, і спосіб розв'язування задачі.
Формули для визначення шуканого елемента дають можливість узагальнити і повніше дослідити знайдену відповідь.
Користуючись алгебраїчним методом, легше визначити умову можливості існування розв’язків даної задачі, виявити їх кількість і деякі характерні особливості кожного розв'язку. Крім того, можна зводити різні задачі геометричного характеру до розв'язування і дослідження алгебраїчних рівнянь, а це, в свою чергу, дає змогу з'ясувати властивості креслярських інструментів і можливості виконання ними тих чи інших побудов.
Знайдена після розв’язування рівняння формула часто вказує на спосіб її побудови.
Отже, алгебраїчний метод є найдійовішим у розв'язуванні питання про можливість виконати ту чи іншу побудову за допомогою циркуля й лінійки, і саме в цьому полягає його найважливіше теоретичне значення.
Проте алгебраїчний метод не розкриває геометричної суті розв'язування задачі. До того ж ми за необхідністю вводимо до малюнка допоміжні відрізки, кути, дуги, кола, чим затушовуємо геометричний зміст знайденого розв'язку.
Завершальним етапом розв'язування будь-якої геометричної задачі на побудову алгебраїчним методом є побудова виведеної алгебраїчної формули. Тому приділяємо увагу виробленню в учнів умінь будувати відрізки, задані найпростішими алгебраїчними формулами. Найпростіші формули, до яких зводиться побудова відрізків при розв’язуванні задач на побудову, такі:
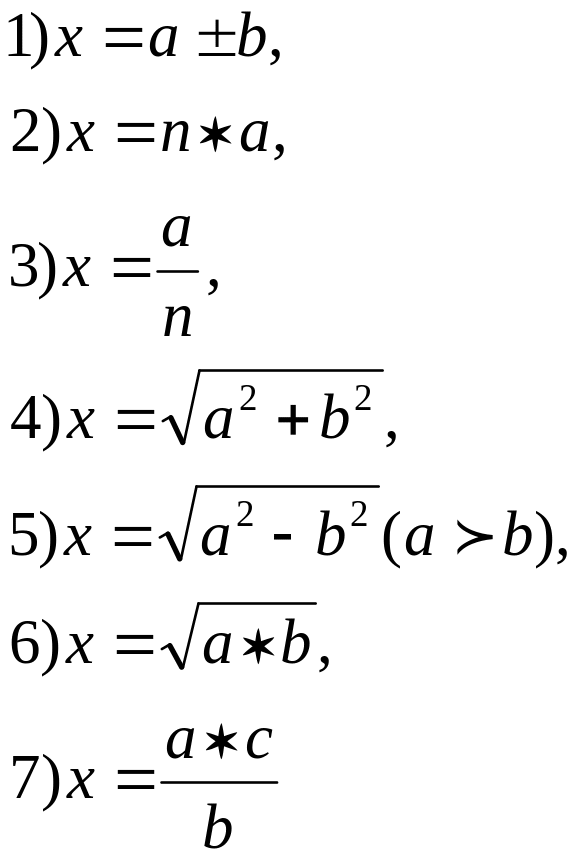
Побудови 1) – 7) розглядаємо в 7-8 класах під час вивчення відповідного геометричного матеріалу та розв'язування задач.
Розділ III. Методичні розробки планів-конспектів уроків геометрії в 7-8 класах з ілюстрацією застосування різних методів геометричних побудов