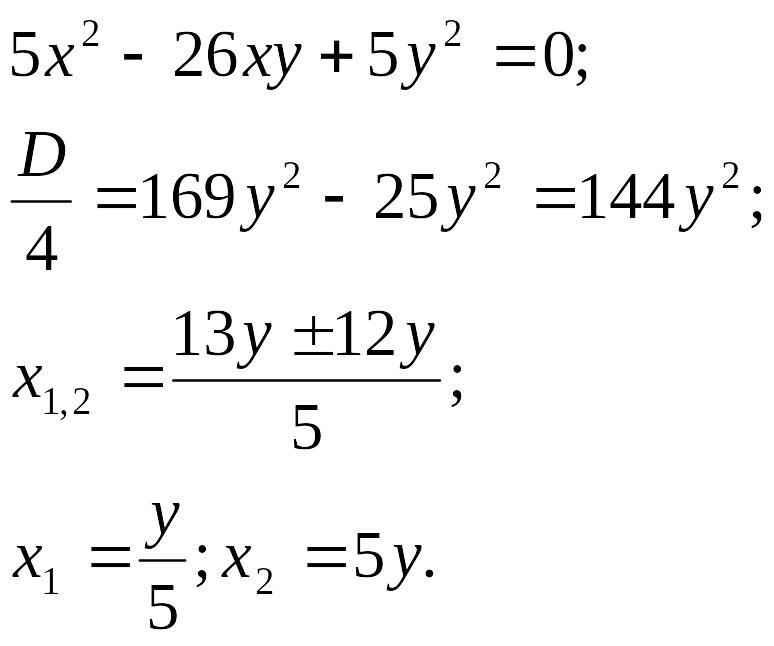3.1. Розв’язок типового варіанту

1.Чи є симетричними такі многочлени?

Виконуємо перестановку . Отримали: . Як бачимо, . Отже, - симетричний многочлен.

2. Доповнити даний многочлен найменшим числом многочленів, щоб він став симетричним.

Виконуємо перестановку . Отримали: Легко побачити, що до другого слід додати . Тоді . А . Тепер . Отже, - симетричний.

3. Виразити через елементарні симетричні многочлени такі многочлени.

.

I спосіб. Перетворимо многочлен:

Працюємо з кожним многочленом окремо:

1)

Система показників вищого члена		Вищий член	Відповідний елементарний симетричний многочлен
3	1
2	2

Знаходимо коефіцієнт :

1	1	2	1	2=4+ =-2

Отже, .

2)

Система показників вищого члена		Вищий член	Відповідний елементарний симетричний многочлен
2	0
1	1

Знаходимо коефіцієнт .

1	1	2	1	2=4+ =-2

Отже,

Тепер .

II спосіб

Відповідь:

4. Розв’язати систему рівнянь.

Вводимо нові змінні . Тоді для нових невідомих отримали наступну систему рівнянь:

Тепер розглядаємо три випадки:

1)

Оскільки то та

2) система не має розв’язків;

3)

Отримуємо, що тобто дана система має розв’язок будь-яку пару чисел, що задовольняє умові .

5. Розв’язати систему рівнянь, ввівши нові допоміжні невідомі.

Введемо нову допоміжну змінну: .

Тоді: . Оскільки то

Виразимо та розв’яжемо рівняння:

Отримали нову систему:

Отже, отримали: та

Якщо повернутися до заміни, то одержимо:

та .

6. Розв’язати рівняння.

Робимо заміну: .

Підносимо до квадрата обидва рівняння системи: .

Склавши їх, отримаємо:

Тоді маємо:

Оскільки , то

Підставимо й розв’яжемо квадратне рівняння:

Отож, отримали дві системи:

та

Повертаємося до заміни:

1)

Отже, та

2)

Отож, та

Відповідь: , , ,

7. Розв’язати зворотне рівняння.

Це зворотне рівняння непарної степені. Згідно з теоремою його ліва частина ділиться на . Отримуємо:

Таким чином, отримали два рівняння:

Друге рівняння – зворотне рівняння парної степені. Перетворюємо його ліву частину:

Так як не є коренем даного рівняння, то ми прийдемо до наступного рівняння відносно :

Таким чином, ми маємо корінь й ще чотири, які легко знайти розв’язавши біквадратне рівняння відносно :

Отож,

Це означає, що для знаходження коренів заданого рівняння слід розв’язати п’ять рівнянь: 1)

2)

3)

4)

5)

Таким чином,

8. Розкласти на множники многочлени.

Перетворимо даний многочлен:

Отримали многочлен другого степеня, який легко розкласти відносно на множники:

Тоді: .

Підставляючи значення , отримаємо:

Розв’яжемо кожне рівняння окремо відносно :

Тоді

Відповідь:

9. Розв’язати задачу про квадратне рівняння.

Скласти квадратне рівняння коренями якого є числа: де – корені квадратного рівняння

Для розв’язування використовуємо формули Вієта, згідно з якими та

З іншого боку, за тими ж формулами:

Таким чином, і тому шукане квадратне рівняння має вигляд

10. Довести, що при будь-яких дійсних та , які задовольняють нерівність , справедлива нерівність .

З умови задачі ми маємо:

(адже ).

Так як за умовою задачі , то нерівність доведено.