Міністерство освіти і науки України

Харківський національний педагогічний університет

ім. Г.С.Сковороди

кафедра математики

КУРСОВА РОБОТА

“Симетричні многочлени”

Виконала:

студентка фізико-математичного

факультету

3 курсу, гр. 3МІ

Стогній Надія Петрівна

Науковий керівник:

доцент, кандидат

фізико-математичних наук

Пуди А.Ю.

Харків – 2008р.

ЗМІСТ

ВСТУП …………………………………………………………………….3

РОЗДІЛ І. СИМЕТРИЧНІ МНОГОЧЛЕНИ ВІД ДВОХ ЗМІННИХ...............................................................................................................5

1.1 Означення і основні властивості……………………………………..5

1.2 Основна теорема про симетричні многочлени від двох змінних ….7

1.3 Теорема про єдиність зображення симетричних многочленів через елементарні симетричні многочлени …………………………………………10

РОЗДІЛ ІІ. ЗАСТОСУВАННЯ СИМЕТРИЧНИХ МНОГОЧЛЕНІВ В ЕЛЕМЕНТАРНІЙ АЛГЕБРІ ..............................................................................14

2.1 Розв’язування системи рівнянь …………………………………….14

2.2 Розв’язування ірраціональних рівнянь …………………………….16

2.3. Зворотні рівняння……………………………………………………17

2.4. Розклад симетричних многочленів на множники………………….21

2.5. Задачі про квадратні рівняння……………………………………....23

2.6. Нерівності…………………………………………………………….24

РОЗДІЛ III. ЗАВДАННЯ ДЛЯ САМОСТІЙНОГО РОЗВ’ЯЗУВА –

ННЯ………………………………………………………………………………26

3.1. Розв’язок типового варіанту………………………………………...29

ВИСНОВКИ………………………………………………………………38

ЛІТЕРАТУРА……………………………………………………………..39

ВСТУП

Одним із найскладніших розділів алгебри для школярів є розв’язування системи рівнянь вищих степенів. Звичайно намагаються розв’язати їх за допомогою якогось штучного прийому. Але загальних правил пошуку для цього не існує. Кожна система розв’язується своїм методом і досвід, який отриманий, мало допомагає при розв’язуванні наступної. В результаті цей розділ шкільної математики перетворюється в набір головоломок.

Тому в роботі розкрито один доволі загальний метод розв’язування систем рівнянь вищих степенів. Він не досить універсальний, але його можна застосувати до більшості систем, з якими стикається учень. Метод, про який йде мова, оснований на теорії симетричних многочленів. Ми побачимо, що теорія досить проста і що вона дозволяє розв’язувати не лише системи алгебраїчних рівнянь, а й різноманітні задачі алгебри (розв’язування ірраціональних та зворотних рівнянь, доведення нерівностей, розклад многочленів на множники в області дійсних чисел і т.д.).

Вважаю, що тема курсової роботи про симетричні многочлени є актуальною.

Об’єктом дослідження є симетричні многочлени від двох змінних, за допомогою яких спрощується розв’язання ряду задач і що, найголовніше, проводиться стандартним шляхом.

Предметом дослідження є вивчення властивостей симетричних многочленів та їх застосування при розв’язуванні відповідних задач.

Звідси випливає головна мета дослідження, яка полягає в тому, що необхідно виявити основні властивості й визначити коло задач, які розв’язуються за допомогою симетричних многочленів.

Для досягнення мети визначаються наступні завдання дослідження: з'ясувати основні властивості квадратних рівнянь, скласти алгоритм розв’язування ірраціональних рівнянь на основі прикладу, з'ясувати вплив дискримінанта при доведенні нерівностей, скласти таблицю обернених симетричних многочленів, підібрати задачі для самостійного розв’язування і навести розв'язок типового варіанту.

Розділ I. Симетричні многочлени від двох змінних

1.1.Означення і основні властивості

Кільцем многочленів від n змінних х₁, х₂, ... , х_n-1, х_n над областю цілісності R називається кільце многочленів від змінної х_n над кільцем , тобто = (1)

Це означення має індуктивний характер. При воно зводиться до означення кільця многочленів від однієї змінної над областю цілісності R (природно вважати, що при ). Якщо ж уже означено кільце при , то за допомогою (1) дістанемо означення кільця. Отже, для довільного натурального означено кільце многочленів від змінних .

Важливим класом многочленів від кількох змінних є клас так званих симетричних многочленів.

Многочлени, в яких та входять однаковим чином, називаються симетричними. Точніше кажучи: многочлен називається симетричним відносно змінних , якщо внаслідок довільної перестановки змінних утворюється многочлен, який дорівнює даному.

Многочлен є симетричним, бо в результаті заміни отримаємо многочлен, який дорівнює даному. І навпаки, поліном не є симетричним: при такій заміні він перетворюється в , що не співпадає з даним.

Симетричні многочлени та являються найпростішими. Їх називають елементарними симетричними многочленами від і . Для них використовують спеціальні позначення:

Крім та , часто використовують так звані степеневі суми, тобто многочлени Прийнято позначати многочлен через . Таким чином,

Встановимо тепер деякі основні властивості довільних симетричних многочленів.

1.Сума, різниця і добуток симетричних многочленів над деяким полем Р є знову симетричними многочленами над цим полем.

Це твердження очевидне.

Наслідок. Множина всіх симетричних многочленів над полем Р утворює область цілісності з одиницею відносно дій додавання і множення.

Зрозуміло, що це кільце є підкільцем всіх многочленів над полем Р.

2.Якщо симетричний многочлен містить деякий член (2), то він містить і член, утворений з (2) внаслідок будь-якої перестановки показників l₁, l₂,…,l_n.

Оскільки, як відомо, від довільної перестановки показників до будь-якої іншої перестановки цих показників можна перейти за допомогою скінченого числа транспозицій, то досить показати, що при транспозиції довільних двох показників степенів у члені (2) ми дістанемо знову деякий член симетричного многочлена . Виконуючи, наприклад, транспозицію показників та , матимемо член . (3)

За означенням симетричного многочлена .

Але другий з цих многочленів повинен містити член (3), бо його дістаємо з члена (2) заміною на і навпаки. Тому внаслідок єдиності канонічної форми і даний многочлен повинен містити член (3).

Наслідок. Якщо (4) є вищий член симетричного многочлена, то

Справді, припустимо супротивне, тобто при якомусь . На підставі властивості 2 даний многочлен разом з членом (4) містить і член (5)

Але з умови випливає, що член (5) вищий за член (4), тобто член (4) не може бути вищим у многочлені. Ця суперечність доводить наше твердження.

1.2. Основна теорема про симетричні многочлени від двох змінних

Існує простий прийом, який дозволяє отримати симетричні многочлени. Візьмемо будь-який (навіть не симетричний) многочлен від і й підставимо в нього замість і їх вираження через і . Зрозуміло, що при цьому отримаємо симетричний многочлен від і . Наприклад, із многочлена отримуємо симетричний многочлен:

.

Виникає питання, чи є цей прийом побудови симетричних многочленів загальним, тобто чи можна за його допомогою отримати будь-який симетричний многочлен?

Розглянутий приклад робить дане припущення вірогідним. Наприклад, степеневі суми досить легко виражаються через і

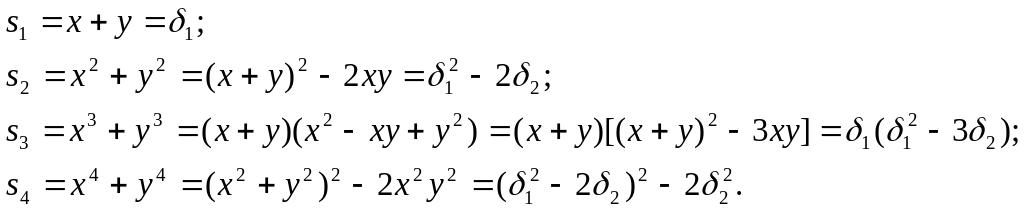
Якщо розглянемо наступні приклади, то отримаємо той самий результат: який би симетричний многочлен ми не взяли, після більш чи менш складних розкладів його вдається виразити через елементарні симетричні многочлени і . Таким чином, приклади приводять нас до припущення правильності наступної теореми.

Теорема. Будь-який симетричний многочлен від і можна представити у вигляді многочлена від та

Зрозуміло, що навіть мільйон прикладів не зможе замінити доведення – завжди залишається ймовірність того, що знайдеться якийсь симетричний многочлен, який не виражається через та .

Перейдемо до доведення теореми. Ми проведемо його в два етапи.