Урок№2/6

Тема№3 «Скорость движения. Средняя скорость. Мгновенная скорость. Равномерное прямолинейное движение. График скорости. График движения.»

1 Равномерное прямолинейное движение.

Прямолинейное движение — это движение, при котором траектория тела (точки) —прямая линия. Примером может служить движение автомобиля по участку дороги, на котором нет подъемов, спусков, поворотов. А прямолинейным равномерным движением называют такое движение, при котором тело (точка) за любые равные промежутки времени совершает одинаковые перемещения.

Для описания прямолинейного движения удобно направить одну из координатных осей, например ось X, вдоль той прямой, по которой движется тело. Тогда координата х будет единственной координатой, которая изменяется при движении. Вектор перемещения при таком выборе оси может быть направлен либо так же, как координатная ось, либо противоположно ей В первом случае проекция s_x вектора s₂ положительна и равна модулю вектора: s_2x = s₂ Во втором она отрицательна и равна S₃x= —S₃.

2 Скорость.

Как найти (вычислить) перемещение тела за какой-то промежуток времени t? Для этого нужно знать перемещение тела за одну единицу времени. Если за t единиц времени совершено перемещение s, то отношение показывает, какое перемещение совершает тело в одну единицу времени. Это отношение называют скоростью движения тела и обозначают буквой v:

υ = s : t (1)

Скоростью равномерного прямолинейного движения называют постоянную векторную величину, равную отношению перемещения тела за любой промежуток времени к значению этого промежутка.

Зная скорость v, мы найдем и перемещение за любой промежуток времени t:

s = υ t (2)

Направлен вектор скорости так же, как вектор перемещения. Направление вектора скорости — это и есть направление движения тела.

При вычислениях перемещения и скорости пользуются формулами, в которые входят не векторы, а их проекции на оси (или ось) координат. Проекции векторов — величины скалярные, поэтому над ними можно производить алгебраические действия. Так как векторы s и vt равны, то равны и их проекции на ось X. Поэтому формула (1а) в скалярной форме записывается так:

s_{x =} υ_x t (3)

Теперь, используя формулы 1, 2 и 3, можно вычислить координату х тела в любой момент времени t:

х = х₀+ υ_хt (4)

Таким образом, мы нашли, как координата х тела зависит от времени t. А это и есть решение основной задачи механики.

3 График движения.

Формула х = х_о + v_xt показывает, как с течением времени изменяется координата тела (точки) при прямолинейном равномерном движении. Она, как говорят, описывает движение. Но описать движение тела можно и с помощью графика.

Если по горизонтальной оси (оси абсцисс) откладывать в выбранном масштабе время, прошедшее с начала отсчета времени, а по вертикальной оси (оси ординат) — тоже в определенном масштабе — значения координаты тела, то полученный график показывает, как изменяется координата тела со временем.

Допустим, что тело (точка) движется по некоторой прямой, вдоль

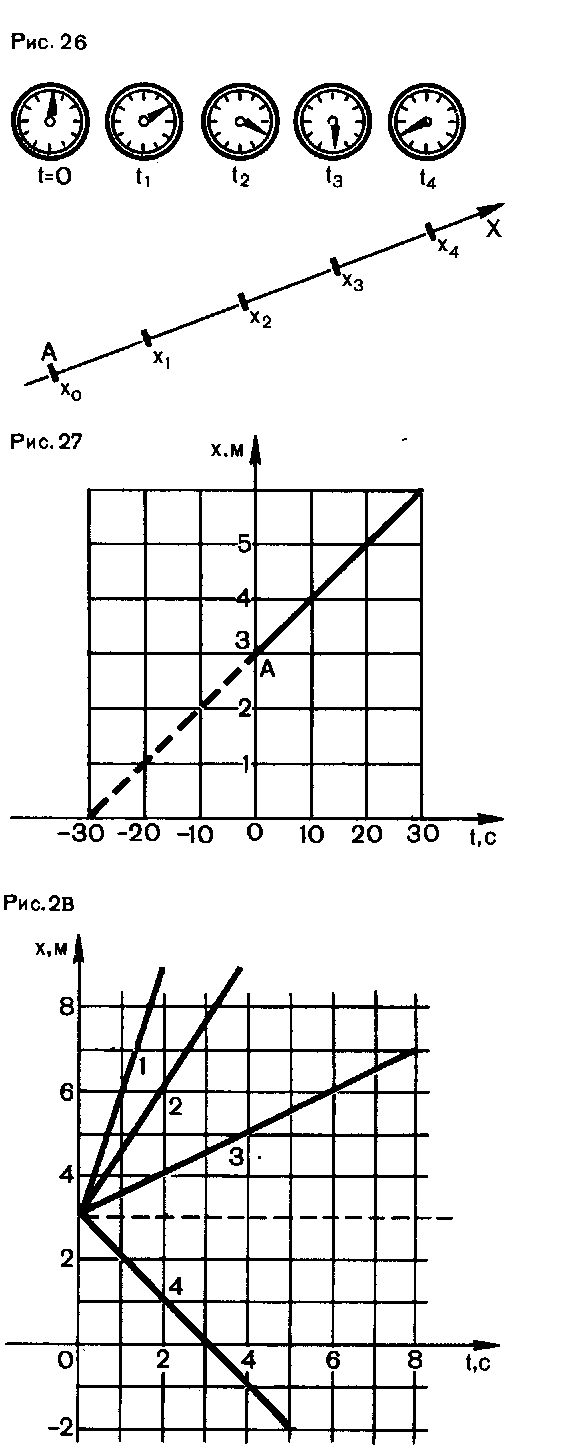
которой мы направим и ось координат X. Значит, при движении изменяется только координата х. Пусть в начальный момент времени t = О и моменты времени t₁ = 10 с, t₂ = 20 с, tз=30 с и т. д. тело находилось в точках, координаты которых соответственно равны: x₀ = 3 м, x₂=4 м, x₃ = 5 м и т.д. (рис. 26).

Отложив по оси абсцисс время и по оси ординат координаты тела (рис. 27), получим график зависимости координаты тела от времени. Такой график называют графиком движения. Для нашего случая прямолинейного движения он представляет собой прямую линию. Другими словами, координата линейно зависит от времени.

График движения (см. рис. 27) не следует путать с траекторией движения (см. рис. 26), которая в нашем случае тоже прямая линия.

График движения есть такое же полное описание движения, как и формула (4). По графику, как и по формуле, можно найти координату тела в любой момент времени, в том числе и в моменты времени, предшествовавшие начальному моменту t=0 (если предположить, что тело двигалось с такой же скоростью и до начала отсчета времени). Например, продолжим график (см. рис. 27, штриховая линия) в сторону, противоположную направлению оси абсцисс (времени), и увидим, что за 30 с до того, как тело оказалось в точке А, оно находилось в точке начала отсчета координаты (x = 0).

По виду графиков движения можно судить не только о координате тела, но и о его скорости. Чем круче график движения, т. е. чем больше угол между ним и осью абсцисс, тем больше скорость движения. На рисунке 28 показано несколько графиков движений. Они относятся к движениям с различными скоростями. Графики 1, 2 и 3 показывают, что тела движутся вдоль оси X в положительном направлении оси X. Тело, график движения которого прямая 4, движется в направлении, противоположном направлению оси Х.

Из графиков движения можно найти и перемещение тела за любой промежуток времени. Из рисунка 28 видно, например, что тело, график движения которого обозначен цифрой 3, за первые 4 с совершило перемещение в положительном направлении оси X, по модулю равное 2 м. За это же время тело, движущееся по графику 4, ,переместилось в противоположном направлении на 4 м.