Глава 6

Использование методов факторного анализа и многомерного шкалирования для выявления первичных (базисных) способностей

Нагруженность одного теста многими факторами является прин­ципиальной особенностью всех практически применяемых тестов и всех моделей многофакторной теории интеллектуальных способно­стей. Это, с одной стороны, делает теорию более адекватной практиче­ским задачам и реально существующим ситуациям, но с дру­гой — сильно усложняет задачу интерпретации результатов измере­ния выраженности интеллектуальных способностей. Ясно, что опи­санные в предыдущем разделе факторы могут рассматриваться и как первичные, и как производные. Действительно, фактор вербального понимания может быть определен через факторы памяти, ассоциатив­ного мышления, индуктивности; числовой фактор — через факторы памяти, пространственно-схематической ориентации, вербального по­нимания. Подобная картина имеет место и при рассмотрении других факторов.

Таким образом, выявление первичных (базисных) интеллектуаль­ных способностей представляет собой сложную задачу. Причем при решении этой задачи естественно появляется возможность «сжатия» информации. Это делает результат тестирования более обозримым, более удобным для интерпретации.

Одним из наиболее эффективных и применяемых сегодня средств «сжатия» информации является комплекс методов факторного анали­за. В основе множества моделей современного факторного анализа ле­жит одна общая идея, которая, как показала практика обработки боль­ших массивов эмпирических данных, является действенной в самых различных областях человеческой деятельности — психологии, меди­цине, экономике, социологии [6, 72—80].

Эту идею составляет предположение о возможности выявления малого числа существенных, базисных параметров на основании ана-108 лиза большого количества «внешних», «косвенных» измерений. При этом, как правило, оказывается, что многие из измеряемых в экспери­менте параметров являются сильно коррелирующими друг с другом. С другой стороны, «внутренние», существенные параметры часто явля­ются трудно измеримыми и могут быть вычислены только на основа­нии анализа массивов измеряемых параметров (рис. 44).

В процессе психологического тестирования измеряемыми пара­метрами являются реакции испытуемых. «Внутренние», существен­ные параметры, которые выявляются в процессе анализа результатов тестирования, в факторном анализе обозначаются как факторы. В ка­честве примеров таких факторов могут быть названы уровень матема­тических или художественных способностей, тип темперамента, уро­вень мотиваций и т.д.

В общем случае удобно представить, что в результате применения некоторого количества различных тестов («) на некоторой совокупно­сти испытуемых (7V) мы получаем массив данных, матрицу Z=(N x п). Пусть строки этой экспериментальной матрицы соответствуют раз­личным наблюдаемым объектам (т. е. испытуемым), а столбцы — па­раметрам, описывающим состояние объектов (т. е. реакции испытуе­мых на тесты), — таблица 4. В такой матрице каждый элемент Ука­зывает значение, которое принимает/-Й параметр на /-м объекте, т.е. результат, который показывает г-й испытуемый в результате примене­ния у-го теста.

Существенно отметить, что столбцы матрицы, являясь результата­ми применения тех или других тестов, имеют, вообще говоря, различ­ный смысл. Ввиду этого, как правило, матрицу данных (Z) приводят к стандартизированному виду (матрице X), что связано с переходом к стандартной нормированной шкале измерений.

Отметим также, что возможны две геометрические интерпретации матрицы исходных данных. По одной можно рассматривать Л'-мерное пространство, оси которого соответствуют отдельным параметрам или факторам. Каждая строка при этом имеет смысл вектора в про­странстве параметров. При этой интерпретации мы имеем возмож-

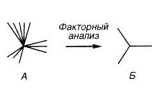
Р и с. 44. Основная идея методов факторного анализа — выявление малого числа базисных (существенных) факторов на основании измерения и обработки большого числа косвенных параметров. А.

«Косвенные», легко измеряемые характеристики представляют собой группы параметров с сильно и слабо д 6 коррелирующими свойствами. Б. «Базисные» параметры (факторы) появляются после «сжатия» исходной информации

ность сравнивать близость реакций всех испытуемых в пространстве N параметров.

По другой интерпретации можно рассматривать TV-мерное про­странство, оси которого соответствуют отдельным объектам (испыту­емым). В таком пространстве объектов каждый параметр (т. е. тест) представляется вектором. Это пространство является пространством объектов и удобно в связи с тем, что в нем имеется возможность срав­нения близости отдельных тестов в «пространстве испытуемых».

Таблица 4. Структура матрицы экспериментальных данных

Важным шагом в моделях и методах факторного анализа является переход от стандартизированной матрицы данных X размерности N* п к квадратной корреляционной матрице R, размерности пхп. Элементы матрицы R представляют собой коэффициенты корреляции r(j,k) между соответствующими параметрами (результатами тестиро­вания) У и jr.

го.к) = аЩщщ *

где У х —векторы, обозначающие у и к столбцы матрицы X.

Факт близости коэффициента корреляции к 1 говорит о малом от­личии значений параметров в среднем на различных объектах, что не исключает, конечно, того, что значения параметров на некоторых объ­ектах могут отличаться значительно. Факт близости величины к 0 го­ворит, в свою очередь, о малой связи параметров и о малой предсказуе­мости значений одного параметра, исходя из величин другого. Вооб­ще, чем меньше величина I r(j,k)\ (абсолютное значение коэффициента корреляции), тем меньше связаны параметры У У (т. е. соответствую­щие тесты) между собой и, следовательно, тем в меньшей степени по мо>кно предсказать по результатам тестирования одним тестом ре­зультаты тестирования другим.

В свете сказанного основная идея факторного анализа может быть сформулирована следующим образом. Решение задачи сжатия инфор­мации при переходе от большого количества поддающихся измерению параметров к существенно меньшему количеству «скрытых» базис­ных параметров-факторов сводится к нахождению небольшого коли­чества векторов с N компонентами (где N — число строк матрицы дан­ных). Другими словами, решение задачи означает приписывание к ис­ходной матрице небольшого числа новых столбцов, с помощью кото­рых можно хорошо описать все столбцы исходной матрицы. В ходе этой процедуры, естественно, происходит снижение размерности iV-мерного пространства параметров.

Какова же связь между измеряемыми в эксперименте параметрами и факторами. Другими словами, какова связь между измеряемыми функциями и их «глубинными» аргументами. В факторном анализе, как правило, эта связь предполагается линейной:

где x^f — измеряемые параметры, число которых равно п, сц, — коэф­фициенты, подлежащие определению и определяющие нагрузку у"-го параметра на к-тл фактор (факторные нагрузи/* — общие факторы, определяющие базис и участвующие, таким образом, в представлении всех параметров измерения, причем число факторов т всегда меньше, чем и (т < п). — «характерные» факторы, каждый из которых участ­вует в определении только одного, своего параметра. Характерные факторы имеют смысл помехи.

Заметим, что предположение линейности связи между измеряемы­ми параметрами и «глубинными» базисными факторами является су­щественным. Как правило, в факторном анализе общие факторы явля­ются ортогональными. В любой модели факторного анализа цель ра­боты заключается в определении общих факторов и факторных нагру­зок, причем геометрически факторные нагрузки являются проекциями параметров на соответствующие общие базисные факторы.

Важно отметить, что в рамках факторного анализа отсутствует од­нозначное определение набора общих (базисных) факторов, удовлет­воряющих данному эмпирическому материалу. В общем случае общие факторы определяются косвенным образом. Вначале непосредственно вычисляются факторные нагрузки, затем ищутся такие линейные ком­бинации измеряемых параметров, которые в каком-либо смысле явля­ются «хорошими» оценками общих факторов.

Исходя из сказанного, актуальной является задача выбора из мно­жества наборов общих факторов некоторого набора, удовлетворяюще­го целям исследования и интуиции исследователя. Переход от одного набора ортогональных общих факторов (одного базиса) к другому можно представить геометрически как процесс «вращения» первона­чального базиса. В результате этой процедуры, естественно, изменя­ются величины факторных нагрузок, т.е. величины проекций резуль­татов тестирования на оси базисных факторов (рис. 45).

Близкими к методам факторного анализа являются методы много­мерного шкалирования. Основой этих методов в применении к рас­сматриваемым нами задачам также является цель понижения размер­ности пространства измеряемых параметров и выделения «первич­ных» интеллектуальньгх способностей. Главное отличие метода за­ключается в том, что при многомерном шкалировании вместо корреля­ционной матрицы используется матрица сходства объектов. Процеду­ра составления такой матрицы заключается в том, что испытуемый ин­туитивно оценивает степень различия (сходства) между теми или ины­ми объектами. При этом считается, что в своих суждениях человек не­явно использует базисные признаки.

Например, при сравнении множества людей по их способности к решению задач может быть получена матрица близости, на основании анализа которой появляется возможность выявления факторов интел­лекта. Другой пример — выявление степени различия (сходства) меж­ду разными типами животных и птиц. Испытуемые на основании сво­их интуитивных правил оценивают попарное сходство между исход­ными объектами. В итоге в результате формирования матрицы сходст­ва становится возможным, как и в первом случае, ввести некоторую метрику, количественно описывающую близость исходных объектов. Причем такая метрика будет описывать близость между объектами в

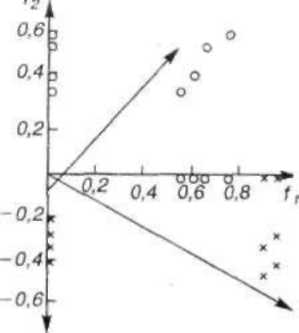
Рис. 45. Вращение ортогонального базиса факто­ров. Результаты тестирования (значения парамет­ров) показаны в пространстве двух факторов/] и/₂. Исходные факторы представлены сплошн^гми ли­ниями, вторичные — пунктиром. Проекции резуль­татов тестирования на исходные факторы показаны как незаполненные и на повернутые факторы — как заполненные кружки. Из рисунка видно, что в ре­зультате поворота уменьшились значения нагрузок на фактор/i, т.е. он теперь имеет меньшее значе­ние при интерпретации результатов тестирования (6, 124) некотором многомерном пространстве, в котором исходные объекты будут представлены точками, расстояния между которыми определя­ются в соответствии со степенью их интуитивной близости.

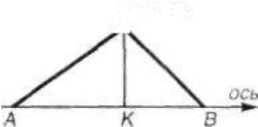
Рассмотрим несколько подробнее процедуру построения такого пространства и процедуру выделения на нем отдельных факторов или шкал. Допустим, имеется матрица сходства между Лоточками. Возь­мем любые три из Л^ги проверим, лежат ли они на одной прямой, т. е., другими словами, могут ли они быть объединены одним фактором (осью, шкалой).

Идея проверки заключается в проведении через две точки (А и В) оси и измерении расстояний АВ, АС и СВ. Если при этом АВ=АС+СВ, то точка С лежит на оси, если АВ<АС+СВ, то нет. В этом случае можно оценить величину перпендикуляра СК от С до оси и, если СК больше некоторого порогового значения, ввести вторую ось, ортогональную первой (рис. 46). Введение последующих осей-факторов проводится аналогичным образом путем перебора точек из N. Расчетные процеду­ры при этом, естественно, усложняются, а степень наглядности умень­шается.

Приведенная процедура, несмотря на упрощенность и неунивер­сальность, ясно показывает, про крайней мере, одну существенную особенность анализа — необходимость проведения смысловой ин­терпретации полученных осей или факторов. Действительно, пусть в результате работы мы смогли описать множество тестов в двухфак-торном пространстве, как линейные комбинации этих факторов. Од­нако процедура факторного анализа (или равно многомерного шка­лирования) ничего не говорит нам о том, чем являются выделенные оси (рис. 47).

Предположим, что в рассмотренном выше примере с животными разных типов все точки, т. е. все объекты сравнения, удалось расположить на плоскости. Таким образом, в результате проведенной процедуры исходное неопределенно большое количество параметров, на основании которых j°^{Cb 3}

люди обычно описывают животных, удалось свести к двум гипотетическим базисным факторам (любая точка плоскости описывается в пространстве двух осей —х, у). Одна­ко теперь возникает вопрос о том, как интер- Рис. 46. Геометрическая ил-претировать содержательный смысл оси х и ^{люстрация идеи} отдельных шкал (базисных факторов) в процессе много-

^{выявления}

оси У? В данном примере ось х может, напри-

мер, иметь смысл размера животного, а ось у мерного

шкалирования (по смысл длины передних конечностей.

40, 7-33)

Рис. 47. Основные этапы процедур понижения раз- случае выглядит как мерности массивов экспериментальных данных

«вращение» первона­чального набора. При этом для определения «истинного» базиса необходимо проведение со­держательного анализа групп измеряемых параметров, имеющих сильную корреляцию (или степень сходства). Отметим, что весьма ес­тественной является ситуация, в которой в принципе удобно ввести неортогональные, т.е. взаимозависимые, оси, так как именно при этом оси приобретают однозначную, осмысленную интерпретацию.

Можно предположить, что в рассматриваемом примере поворот осей на определенный угол или же введение каких-то двух неперпен­дикулярных (неортогональных) осей даст возможность провести но­вую, более хорошую интерпретацию смысла этих осей.

Подводя итог рассмотрения методов факторного анализа и много­мерного шкалирования, заметим, что сущность этих методов сжатия информации заключается в выявлении скрытых корреляционных от­ношений между различными измеряемыми параметрами. Другими словами, в выявлении таких измерений, результаты которых могут быть хорошо предсказуемы на основании других измерений. Таким образом, происходит выявление тесно связанных групп измерений, что и является основой эффекта понижения размерности массивов изучаемых параметров. Однако такие процедуры в лучшем случае только подготавливают почву для выявления действительно глубин­ных базисных компонент, лежащих в основе формирования различ­ных групп интеллектуальных и творческих способностей.

Выявление корреляционных отношений само по себе автоматиче­ски не обеспечивает обнаружение причин, лежащих в основе форми­рования отдельных групп сильно связанных параметров. И это, по-видимому, является принципиальным ограничением возможностей дан­ных методов. Возможно, дальнейшее продвижение к цели выявления базисных характеристик, определяющих способности человека, связа­но с изучением психофизиологических закономерностей осуществле­ния тех или иных тестовых функций.