3. Приклади розв’язування задач.

Задача 1. На основі даних про роздрібний товарооборот та доходи населення у грошових одиницях побудувати економетричну модель роздрібного товарообігу. Вихідні дані наведені в табл.1.1.

Таблиця 1.1.

№ з/п	Роздрібний товарообіг	Доходи населення
1	17	18
2	18	20
3	19	21
4	20	22
5	21	24
6	23	25
7	24	27
8	25	28
9	26	29
10	27	31

Розв’язання.

1. Ідентифікуємо змінні:

У- роздрібний товарообіг (залежна змінна);

Х- доходи населення (незалежна змінна).

2. Специфікуємо економетричну модель у лінійній формі:

, де

- параметри моделі (оцінка економетричної моделі),

- стохастична складова (залишки).

3.Оцінимо параметри моделі за методом 1 МНК. Модель розглядатимемо у вигляді:

, де

- очікуваний товарообіг, - очікувані параметри.

Для цього запишемо систему нормальних рівнянь:

І=1,…n, n=10 – кількість спостережень.

Для розв’язання системи (1) відносно складемо розрахункову таблицю.

Таблиця 1.2.

№ з/ п	Y	X		XY
1	2	3	4	5	6	7	8	9	10	11	12	13
1	17	18	324	306	16,67	-6,5	-5	42,25	32,5	0,33	0,1089	25
2	18	20	400	360	18,31	-4,5	-4	20,25	18,0	-0,31	0,0961	16
3	19	21	441	399	19,13	-3,5	-3	12,25	10,5	-0,13	0,0169	9
4	20	22	484	440	19,25	-2,5	-2	6,25	5,0	0,05	0,0025	4
5	21	24	576	504	21,59	-,05	-1	0,25	0,5	-0,59	0,3481	1
6	23	25	625	575	22,41	0,5	1	0,25	0,5	0,59	0,3481	1
7	24	27	729	648	24,05	2,5	2	6,25	5,0	-0,5	0,0025	4
8	25	28	784	700	24,87	3,5	3	12,25	10,5	0,13	0,0169	9
9	26	29	841	754	25,69	4,5	4	20,25	18,0	0,31	0,0961	16
10	27	31	961	837	27,33	6,5	5	42,25	32,5	-0,33	0,1089	25
	220	245	6165	5523	-	-	-	162,5	133	-	1,145	110

.

.

Стовпчик 6, 11 і 12 заповнюємо після обчислення .

Підставимо в систему (1).

.

Одержуємо систему рівнянь

Отже, економетричну модель роздрібного товарообігу запишемо так:

Розрахуємо 6-й стовпчик для кожного значення із третього стовпчика, наприклад для х=18 маємо

Далі можна розрахувати стовпчики 11 і 12.

4. Параметри можна оцінити альтернативним способом:

Х=22-0,82*24,5=1,91.

5. Обчислити дисперсії залежної змінної та залишків:

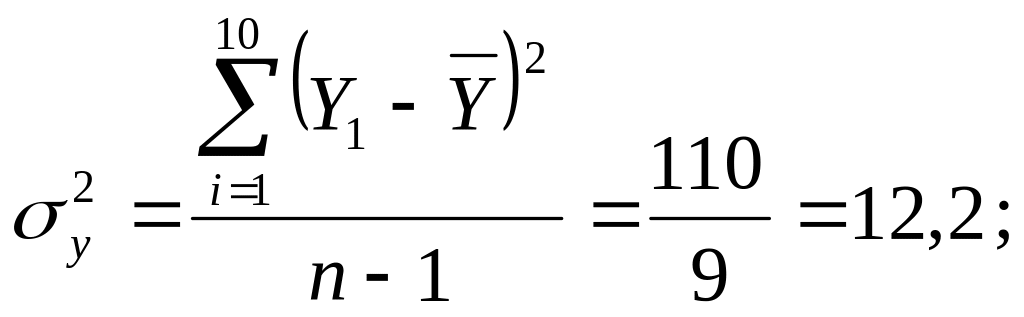
6. Визначимо коефіцієнт детермінації та кореляції:

.

.

Коефіцієнт детермінації свідчить (визначає) про те, що варіація обсягу роздрібного товарообігу на 99% визначається варіацією доходів населення.

Коефіцієнт кореляції R=0,994 показує, що існує тісний зв’язок між цими соціально-економічними показниками.

Нагадаємо, що якщо близький до 1, то можна стверджувати, що зв’язок між змінними є статистично значущим.

Якщо R близький до 1, то існує тісний зв’язок між змінними моделі.

7. Знадимо матрицю С – матрицю похибок. (Матриця похибок обернена до матриці системи (1) нормальних рівнянь).

За методом Джордано-Гауса ми дописали справа одиничну матрицю і перетворимо останню матрицю так, що зліва одержали одиничну матрицю.

Розділимо всі елементи першого рядка на 10:

Перший рядок залишимо без зміни, потім перший рядок множимо почленно на -245 і додаємо до другого. Отримаємо:

розділимо всі елементи другого рядка на 162,5

Другий рядок залишаємо без зміни, потім другий рядок множимо почленно на -24,5 і додаємо до першого. Отримаємо:

Отже, .

8. Визначимо стандартні похибки оцінок параметрів моделі, враховуючи дисперсію залишків та діагональні елементи матриці С:

;

.

Порівняємо стандартні похибки оцінок параметрів моделі зі значеннями цих оцінок. Стандартна похибка оцінки параметра становить : абсолютне значення цієї оцінки (0,82), що свідчить про незміщеність такої оцінки параметра.

Стандартна похибка оцінки параметра становить : абсолютне значення цієї оцінки (1,91). Отже, параметр може мати зміщення, яке зумовлене невеликою сукупністю спостережень (п=10).

9. Висновки. Економетрична модель кількісно описує зв’язок роздрібного товарообігу та доходів населення.

Параметр характеризує граничний розмір витрат на купівлю товарів у роздрібній торгівлі.

Визначимо коефіцієнт еластичності роздрібного товарообігу залежності від доходів населення:

.

Отже, зі збільшенням доходів населення на 1% роздрібний товарообіг зростає на 0,91%.

Задача 2. На середньомісячну заробітну плату впливає ряд чинників. Виділимо серед них продуктивність праці, фондомісткість та коефіцієнт плинності робочої сили. Щоб побудувати економетричну модель заробітної плати від загальних чинників згідно з методом найменших квадратів, необхідно переконатися, що продуктивність праці, фондомісткість та коефіцієнт плинності робочої сили, як залежні змінні модулі – не мультиколінеарні.

Вихідні дані наведені в таблиці 2.1.

Таблиця 2.1.

Номер цеху	Продуктивність праці (люд.-дн.)	Фондомісткість (млн.грн.).	Коефіцієнт плинності робочої сили (%)
1	32	0,89	19,5
2	29	0,43	15,5
3	30	0,70	13,5
4	31	0,61	9,5
5	25	0,51	23,5
6	34	0,51	12,5
7	29	0,65	17,5
8	24	0,43	14,5
9	20	0,51	14,5
10	33	0,92	7,5

Основні теоретичні положення.

Визначення. Мультиколінеарність означає існування тісної лінійної залежності, або сильної кореляції, між двома або більше пояснювальними змінними.

Вона негативно впливає на кількість характеристики економетричної моделі або робить її побудову неможливою.

Основні наслідки мультиколінеарності:

1. Падає точність оцінювання, яка виявляється так:

• Помилки деяких конкретних оцінок стають занадто великими;

• Ці помилки досить корельовано одна з одною;

• Дисперсії оцінок параметрів різко збільшуються.

2. Оцінки параметрів деяких змінних моделі можуть бути незначущими через наявність їх взаємозв’язку з іншими змінними, а не тому що вони не впливають на незалежну змінну. В такому разі множина вибіркових даних не дає змоги цей вплив виявити.

3. Оцінка параметрів стають досить чутливими до обсягів сукупності спостережень збільшення сукупності спостережень іноді може спричинити істотні зміни в оцінках параметрів.

Найповніше дослідити мультиколінеарність можна за допомогою алгоритму Фаррара-Глобера. Цей алгоритм містить три види статистичних критеріїв, згідно з якими перевіряється відповідно мультиколінеарність:

1. Усього масиву пояснюючих змінних ( - «хі-квадрат»),

2. Кожної пояснюючої змінної з рештою пояснювальних змінних (F-критерій),

3. Кожної пари пояснювальних змінних (t – критерій).

Усі критерії при порівнянні з їх табличними значеннями дають змогу зробити конкретні висновки щодо наявності чи відсутності мультиколінеарності пояснюючих змінних.

При розв’язуванні задачі 2 використаємо алгоритм Фаррара-Глобера.

Крок 1. Нормалізація (стандартизація) змінних.

Нехай - вектори пояснювальних змінних. Елементи стандартизованих змінних обчислюємо за формулою:

( або ),

де п – кількість спостережень ( п=10 ),

,

- середнє арифметичне значення Х_к.

- дисперсія змінної Х_к.

Спочатку обчислимо середні арифметичні для кожної пояснювальної змінної:

.

.

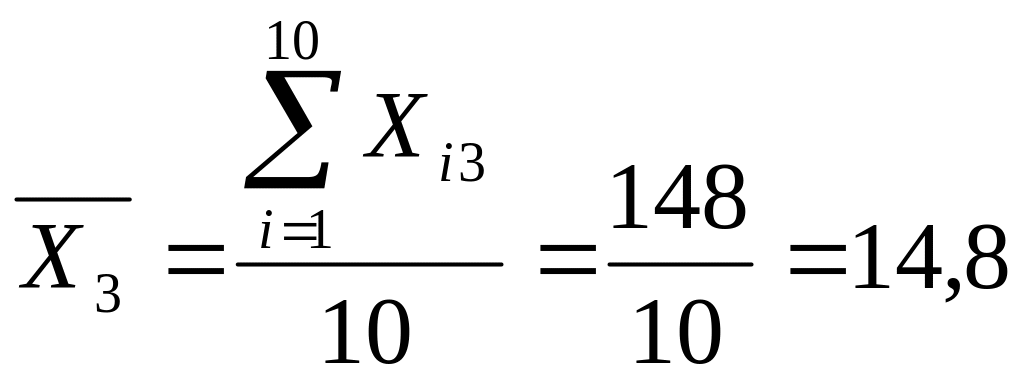Розрахункові дані для стандартизації змінних подані у таблиці 2.2.

Таблиця 2.2.

№ з/п
1	2	3	4	5	6	7	8	9	10
1	3,3	0,274	4,7	10,89	0,0751	22,09	0,2487	0,5249	0,3374
2	0,3	-0,186	0,7	0,09	0,0346	0,49	0,0226	-0,3563	0,0503
3	1,3	0,084	-1,3	1,69	0,0071	1,69	0,0980	0,1609	-0,0933
4	2,3	-0,006	-5,3	5,29	0,00004	28,09	0,1733	-0,0115	-0,3805
5	-3,7	-0,106	8,7	13,69	0,0112	75,69	-0,2788	-0,2031	0,6246
6	5,3	-0,106	-2,3	28,09	0,0112	5,29	0,3994	-0,2031	-0,16541
7	0,3	0,034	2,7	0,03	0,0346	7,29	0,0226	0,0651	0,1938
8	-4,7	-0,186	-0,3	22,09	0,0112	0,09	-0,3542	-0,3563	-0,0215
9	-8,7	-0,106	-0,3	75,69	0,0864	0,09	-0,6556	-0,2031	-0,0215
10	4,3	0,294	-7,3	18,49	0,2726	53,29	0,3240	0,5632	-0,5240
	-	-	-	176,1	-	194,1	-	-	-

Обчислюємо дисперсії кожної незалежної змінної:

;

;

.

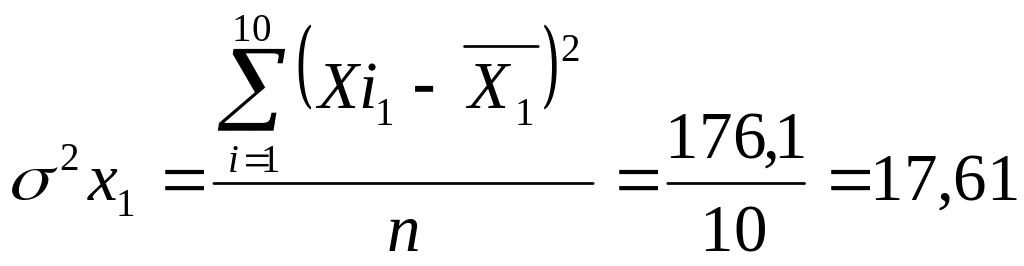Розрахуємо знаменники для стандартизації кожної незалежної змінної:

Для:

Для:

Для:

Далі кожний елемент стовпчика 2 таблиці 2.2. ділимо на 13,27 та заповнюємо стовпчик 8, а кожний елемент стовпчика 3 ділимо на 0,522 та заповнюємо стовпчик 9, і, нарешті, кожний елемент стовпчика 4 ділимо на 13,93 та заповнюємо стовпчик 10.

Елементи стовпчиків 8, 9, та 10 складають матрицю стандартних змінних.

Крок 2. Знаходження кореляційної матриці

,

Де : - матриця стандартизованих (нормалізованих) змінних,

- матриця, транспонована до .

На додатку 1 до задачі 2 показано знаходження елементів матриці r.

Кожний елемент матриці r характеризує тісноту зв’язку однієї незалежної змінної з іншою. Діагональні елементи характеризують тісноту зв’язку кожної незалежної змінної з цією самою змінною, тому вони дорівнюють одиниці. Але за рахунок помилок та зміщеності коефіцієнтів парної кореляції числові значення діагональних елементів можуть наближатися до одиниці. Але за рахунок помилок та зміщеності коефіцієнтів парної кореляції числові значення діагональних елементів можуть наближатися до одиниці. Якщо це так, то вони змінюються одиницями, а інші значення матриці r змінюються на величену, що визначається як різниця між одиницею та діагональних елементом.

Отже.

Крок 3. Обчислюємо детермінант кореляційної матриці .

.

При ступенях свободи і рівні значущості критерій .

отже, в масиві змінних не існує мультиколінеарності.

Крок 4. Знаходимо матрицю, обернену до матриці r:

.

У додатку 2 до задачі 2 пояснено алгоритм обчислення матриці С.

Крок 5. Обчислимо F-критерії, використовуючи діагональні елементи матриці С.

;

;

.

Для рівняння значущості та ступенів свободи чисельника 7, а знаменика 2 дробу табличне значення .

Отже, кожна з пояснювальних змінних не мультиколінеарна з двома іншими. Щоб визначити наявність попарної мультиколінеарності, продовжимо дослідження.

Крок 6. Обчислимо частинні коефіцієнти кореляції, скориставшись елементами матриці С.

;

;

.

Частинні коефіцієнти кореляції показують тісноту зв’язку між двома змінними за умови, що третя не впливає на зв’язок.

Крок 7. Визначимо t-критерій на основі частинних коефіцієнтів кореляції:

;

;

.

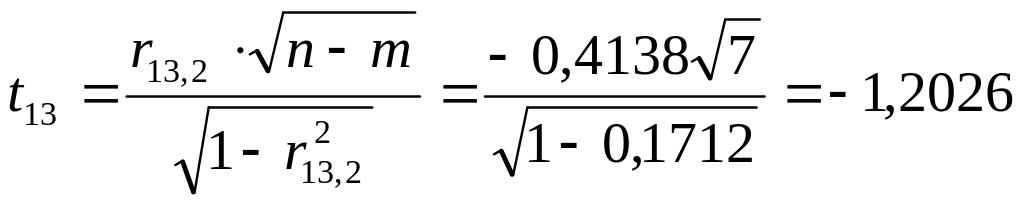Табличне значення t-критерію при n-m=7 ступеннях свободи і рвіні значущості дорівнює 1,69.

Значення обчислення t-критеріїв менше за табличне. Отже, всі пари незалежних змінних не є мультиколінеарними.

Додаток 1 до задачі 2.

1. Матриця, транспонована до .

2. Матриця матиме розмір .

1. 

3.Для обчислення необхідно почленно помножити кожний елемент першого рядка матриці на кожний елемент першого стовпчика матриці і одержані добутки додаємо додати:

4. Для обчислення 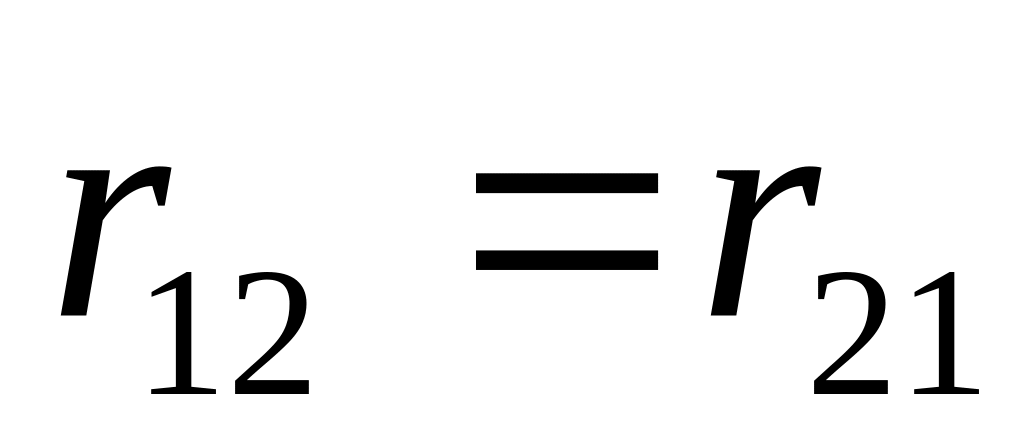кожний елемент першого рядка матриці множимо почленно на елемент другого рядка стовпчика матриці та одержані добутки додаємо:

5.

6.

7. Якщо замінимо одиницями, то інші елементи змінюємо на 1-1,0004=0,0004.

Додаток 2 до задачі 2.

Знаходження матриці С, оберненої до .

Використовуємо алгоритм Йордана-Гуаса. До матриці r дописуємо одиничну матрицю і з допомогою елементарних перетворень дану матрицю матрицю перетворюємо в одиничну.

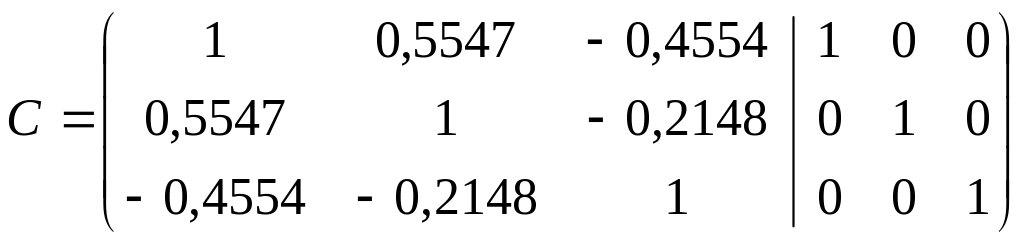
Перший рядок залишаємо без зміни, потім перший рядок множимо почленно на -0,5547 та джодпаємо до другого, далі перший рядок множимо на 0,4554 та додаємо до другого; далі перший рядок множимо на 0,4554 та додаємо до третього. Отримаємо:

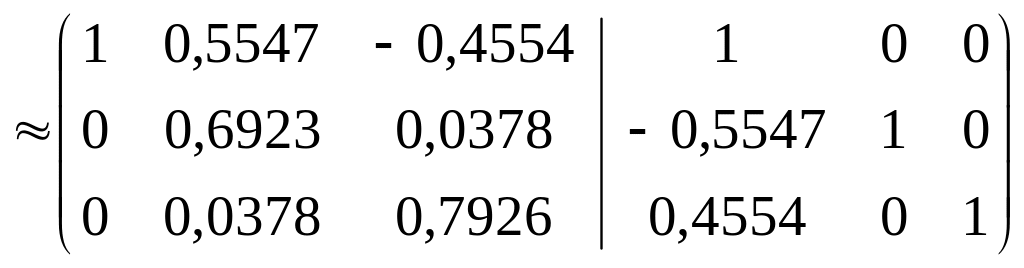
Другий рядок матриці розділимо на 0,6923, одержимо:

Другий рядок залишимо без зміни, потім другий рядок множимо почленно на -0,5547 та додаємо до першого, далі другий рядок множимо на -0,0378 та додаємо до третього. Отримаємо:

Третій рядок розділимо на 0,7905, одержуємо:

Третій рядок залишимо без зміни, потім третій рядок множимо почленно на 0,4857 та додаємо до першого, далі третій рядок множимо на -0,0546 та додаємо до другого. Отримаємо:

Отже,