3 Примеры выполнения заданий из контрольной работы №2

1. Обработка результатов косвенных измерений

3.1.1 Краткие теоретические сведения

Косвенные измерения – это измерения, при которых искомая величина вычисляется по некоторой известной формуле на основе результатов прямых или косвенных измерений величин, связанных с искомой величиной определенной функциональной зависимостью и входящих формулу.

Алгоритм обработки результатов косвенных измерений

Пусть y  измеряемая величина, которая является функцией величин х₁, х₂, … , х_n, найденных в ходе n прямых измерений:

.

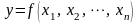Тогда для обработки результата косвенного измерения величины y необходимо:

1. Обработать результаты прямых измерений, задав некоторое значение доверительной вероятности α (например, α = 0,95) и представить их в виде доверительных интервалов:

х₁ = (х₁ ± х₁);

х₂ = (х₂ ± х₂);

…

х_n = (х_n ± х_n).

2. Рассчитать среднее значение величины y как функцию величин <x₁>, <x₂>, ..., <x_n>:

.

3. Рассчитать полуширину доверительного интервала y по формуле (число слагаемых в формуле равно числу переменных):

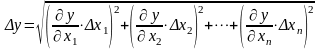, (3.1.1)

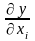
где  частная производная функции по переменной х_i .

В формулу 3.1.1 подставляют значения частных производных, найденные при подстановке средних значений переменных .

4. Записать результат измерений в виде доверительного интервала

y = (y ± y) ед. изм.,  = 0,95.

5. Указать относительную погрешность

.

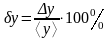3.1.2 Пример выполнения задания

Задача:

Проводник длиной ℓ = (60,0 ± 0,1) м и площадью сечения S = (0,34 ± 0,01) мм² имеет сопротивление R = 3,0 Ом, определённое с относительной погрешностью δR = 2%. Определить (с учётом погрешности) удельное сопротивление проводника.

Р ешение:

Удельное сопротивление проводника рассчитывается по формуле

,

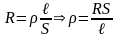т.е. измеряемая величина  является функцией трёх переменных R, S и ℓ

 = f (R, S, ℓ).

Для решения задачи воспользуемся алгоритмом обработки результатов косвенных измерений.

1. Обработаем результаты прямых измерений. Из условия задачи следует, что

<ℓ> = 60,0 м; ℓ = 0,1 м;

<S> = 0,34·10^–6 м²; S = 0,01·10^–6 м²;

<R> = 3,0 Ом; 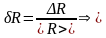R = <R>·δR = 3,0 Ом·0,02 = 0,06 Ом.

2. Найдем среднее значение величины < > по формуле:

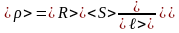
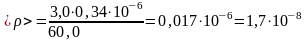(Ом·м).

3. Найдём полуширину доверительного интервала Δ по формуле:

.

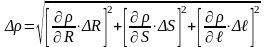Для этого найдём значения частных производных функции < > при средних значениях величин <R>, <S>, <ℓ>:

; ; .

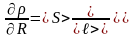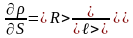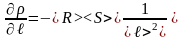Тогда

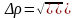
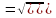
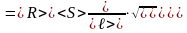
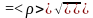
где  R,  S,  ℓ – относительные погрешности.

(Ом·м).

4. Запишем результат измерения:

 = (1,7 ± 0,1)·10^–8 Ом·м,  = 0,95.

5. Укажем относительную погрешность

; .

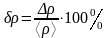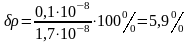3. 2 Графическое представление результатов измерений

3.2.1 Краткие теоретические сведения

Метод наименьших квадратов

При анализе результатов различных экспериментов очень часто возникает необходимость установить вид зависимости какой-либо величины y от величины х. Например, какова зависимость силы тока I в цепи от приложенного напряжения U или какова зависимость производительности труда работника от его заработной платы.

Чтобы установить вид функциональной зависимости y = f(x) производят ряд измерений искомой величины y для нескольких различных значений величины х.

Для наглядности результаты измерений, то есть экспериментальные точки с координатами (x_i, y_i), наносят на координатную плоскость OXY и пытаются подобрать функцию y = f(x), график которой наилучшим образом моделирует (отражает) реальную зависимость величины y от величины х. Этот метод называется аппроксимацией, а найденная приблѝженная к реальной функциональная зависимость – аппроксимирующей.

Существует множество методов нахождения аппроксимирующих зависимостей. Наиболее используемым является метод наименьших квадратов (МНК). Он базируется на следующих основных положениях:

1. Заранее на основании каких-либо предположений (например, на основании научных законов) выбирается общий вид зависимости y = f(x). Очень часто, и в естественных, и в социально-экономических науках в качестве аппроксимирующей выбирается линейная зависимость у = ах + b.

Даже когда зависимость нелинейная (например, зависимость пути S от времени t при равноускоренном движении ), величины, откладываемые по координатным осям, выбирают таким образом, чтобы получить линейную зависимость. То есть, график пути S от времени t при равнопеременном движении строят в осях S = f(t²). Тогда графиком является прямая линия, походящая через начало отсчёта.

2. Аппроксимирующая зависимость у = ах + b является оптимальной (наиболее приближенной к реальной), если сумма квадратов отклонений (расстояний) по вертикали от экспериментальных точек до кривой будет минимальной.

Для построения аппроксимирующей прямой y = ax + b необходимо найти значения углового коэффициента а и параметра b.

При выводе предположим, что погрешности содержат только величины y_i (такое предположение часто оправдывается на практике), иначе вывод значительно усложнится. Пусть отклонение по вертикали экспериментального значения y_i от аппроксимирующей прямой у = ах + b в i-ом (i = 1, 2, 3, ... , n) измерении (при х = x_i) равно

,

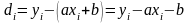тогда, согласно методу наименьших квадратов наилучшим приближением будет такая аппроксимирующая прямая, для которой сумма квадратов отклонений по вертикали от экспериментальных точек до прямой по всем n измерениям будет минимальной, т.е.

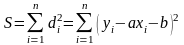 – минимальна.

Для определения значений коэффициентов а и b аппроксимирующей прямой, при которых величина S будет минимальной, найдем частные производные и 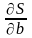и приравняем их к нулю.

Составим систему уравнений:

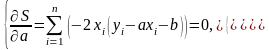; (3.2.1)

Учитывая, что а = Const и b = Const, и, разделив каждое из уравнений системы (3.2.1) на 2, получим

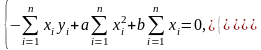
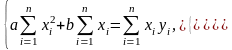(3.2.2)

Коэффициенты а и b найдём решением системы уравнений (3.2.2).

Для нахождения коэффициента а, умножим первое уравнение системы (3.2.2) на n, а второе – на :

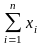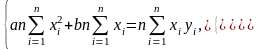(3.2.3)

Вычтем второе уравнение системы (3.2.3) из первого и получим:

,

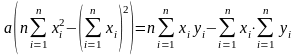откуда коэффициент а:

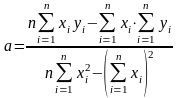. (3.2.4)

Для нахождения коэффициента b, умножим первое уравнение системы (3.2.2) на , а второе – на :

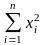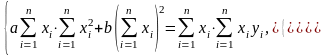(3.2.5)

Вычтем первое уравнение системы (3.2.5) из второго и получим:

,

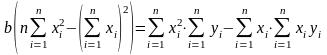откуда коэффициент b:

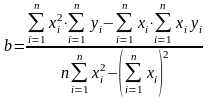. (3.2.6)

Очевидно, что ручная обработка результатов с помощью приведённых формул слишком трудоёмка. При построении графиков "вручную" метод наименьших квадратов используется интегрировано – прямая между экспериментальными точками проводится "на глаз".

3.2.2 Пример выполнения задания

Задача:

Экспериментально снята зависимость величины у от величины х (значения х и соответствующие им экспериментальные значения у приведены в таблице).

x	0	1	2	3	4	5	6	7	8	9
y	2,0	2,4	2,5	3,2	3,8	4,2	4,1	5,0	5,4	6,0

Методом наименьших квадратов определить коэффициенты а и b аппроксимирующей линейной зависимости у = ах + b. На системе координат OXY проставить экспериментальные точки и построить график аппроксимирующей зависимости.

Решение:

Коэффициенты а и b для построения аппроксимирующей линейной зависимости у = ax + b найдем методом наименьших квадратов, используя готовые формулы (3.2.4) и (3.2.6).

Для удобства вычислений заполним таблицу:

i	1	2	3	4	5	6	7	8	9	10
xi	0	1	2	3	4	5	6	7	8	9	45	2025
xi2	0	1	4	9	16	25	36	49	64	81	285	–
yi	2,0	2,4	2,5	3,2	3,8	4,2	4,1	5,0	5,4	6,0	38,8	–
xiyi	0	2,4	5,0	9,6	15,2	21,0	24,6	35,0	43,2	54,0	210	–

где

;

;

;

;

.

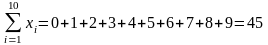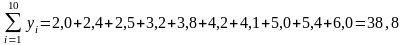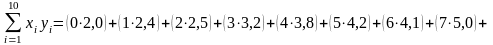
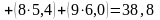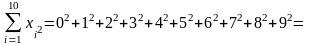
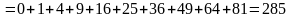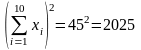Тогда, учитывая, что число измерений n = 10, по формулам (3.2.4) и (3.2.6) найдём коэффициенты а и b аппроксимирующей линейной зависимости:

;

.

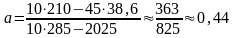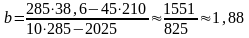Следовательно, аппроксимирующая линейная зависимость имеет вид

у = 0,44x + 1,88.

Для построения графика аппроксимирующей зависимости найдем координаты двух точек А и В, принадлежащих прямой:

	А	В
x	0	9
y	1,88	5,84

Н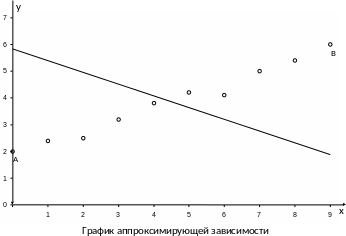 а системе координат OXY проставим экспериментальные точки (обозначены символом «○») и построим график аппроксимирующей зависимости по точкам А и В (обозначены символом «»).