3.4.2. Перевод чисел из одной системы счисления в другую.

Для перевода числа из двоичной системы в десятичную необходимо каждую цифру двоичного числа умножить на ее вес и результаты сложить:

10101111₍₂₎ = 1*2⁷ + 0*2⁶ + 1*2⁵ +0*2⁴ + 1*2³ + 1*2² + 1*2¹ + 1*2⁰ =

= 128 + 32 + 8 + 4 + 2 + 1 = 175₍₁₀₎

Для перевода числа из десятичной системы в двоичную используют метод деления на 2 с остатком. Десятичное число последовательно делится на 2, пока не получится 0. Остатки от каждого деления выписываются в обратном порядке, что схематически показано на рис. 1.2.

А

Число: | остаток от деления на 2 Число: | остаток от деления на 2

43 | 1 22 | 0

21 | 1 11 | 1

10 | 0 5 | 1

5 | 1 2 | 0

2 | 0 1 | 1

1 | 1 0

0 двоичное число: 101011 двоичное число: 10110

Рис. 1.2. Перевод из десятичной системы счисления в двоичную последовательным делением на 2.

налогично осуществляется перевод числа из десятичной системы исчисления в восьмеричную (деление на 8) и в шестнадцатиричную (деление на 16).

Переход от записи чисел в двоичной системе к восьмеричной или шестнадцатиричной и обратно производится по очень простым правилам (рис. 1.3 и 1.4).

Для перехода от двоичной к восьмеричной (или шестнадцатиричной) системе необходимо двигаясь, справа налево, разбить двоичное число групп по три (четыре) разряда соответственно, дополняя при необходимости левую крайнюю группу нулями. Затем каждую группу из трех (четырех) разрядов заменить соответствующей восьмеричной (шестнадцатиричной) цифрой.

Для перевода восьмеричного (шестнадцатиричного) числа в двоичное достаточно заменить каждую цифру указанного числа соответствующим трехразрядным или четырехразрядным двоичным числом. При этом ненужные н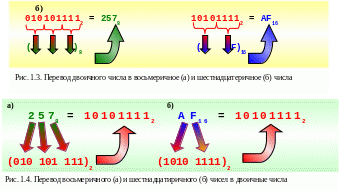 ули слева отбрасываются.

Запись чисел и кодов в восьмеричной или шестнадцатиричной системах содержит меньше цифр. Это преимущество позволяет облегчить программисту написание программ в кодах машинных команд.

3.4.3. Арифметические операции с двоичными числами.

С целью упрощения реализации арифметических операций в компьютере для представления двоичного числа используются прямой, обратный и дополнительный двоичные коды.

Прямой код используется для представления целого двоичного числа в виде:

где  – знаковый разряд (0 – для положительного числа, 1 – для отрицательного числа); a_n – двоичные разряды числа (0 или 1),

Числа Х = – 1101101; Y = 1101101 в прямом коде имеют вид:

Х_пр = 11101101; Y_пр = 01101101

Обратный код используется только для представления отрицательных чисел и образуется путем постановки в знаковый разряд единицы и замены во всех других разрядах числа единиц нулями, а нулей единицами. Например, число Х= – 1101101 в обратном коде будет представлено в виде Х_обр = 10010010. Обратный код, если его рассматривать как число, является дополнением модуля исходного числа без знака, помещенного в разрядную сетку:

Х + Х_обр = 1101101 + 10010010 = 11111111

Дополнительный код числа получают из обратного путем прибавления единицы к младшему разряду. Например, для числа Х= – 01010101

Х_обр = 10101010; Х_доп = 10101011

Обратный и дополнительный коды положительного числа совпадают с представлением самого числа. Для перехода от дополнительного кода к модулю числа выполняются инверсия и добавление единицы в той же последовательности.

При сложении и вычитании чисел они обычно представляются в зависимости от типа арифметико-логического устройства (АЛУ) процессора в обратном или дополнительном коде.

Если в запоминающем устройстве числа представлены в другом коде, то предварительно перед действием алгебраического сложения в АЛУ осуществляется их перевод в необходимый код. После выполнения данной операции результат, если он записывается в оперативную память, снова переводится в код, в котором представлены числа, хранящиеся в запоминающем устройстве.

Таблица сложения:

0 + 0 = 0

1 + 0 = 1

1 + 1 = 10 – перенос в следующий разряд

Таблица умножения в двоичной системе:

0*0 = 0

1*0 = 0

1*1 = 1

Умножение сводится к операциям сдвига и сложения.

Пример:

1 011 1011

1101 +