Термическое равновесие

Показателем термического равновесия в системе служит равенство температур всех ее составляющих. Покажем, что в дуге существует локальное термическое равновесие, которое устанавливается достаточно быстро.

Электроны при плотности тока j от электрического поля Е получают в 1 за 1 с энергию

где – подвижность электрона; ; - время пробега электрона.

При столкновении с тяжелыми S-частицами(ионы, атомы) в плотной плазме вектор скорости электронов претерпевает хаотическое(в среднем равномерное) рассеяние. При этом энергия электронов (кинетическая) переходит в тепловую. Это рассеяние наступает при

Пусть . Сечение Рамзауэра для столкновений электронов с тяжелыми частицам S равно = , а . Тогда для плазмы дуги в Ar получим время пробега =1/( * ) с, т.е.время установления равновесия мало.

Для термического равновесия необходимо, чтобы отношение (где - энергия, получаемая электроном от поля на участке пробега ; ; - энергия теплового движения электрона) и относительная разность температур были значительно меньше единицы, т.е.

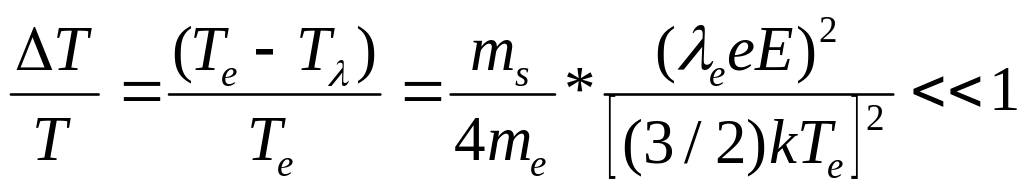
Так как , то

т.е. в основном определяется отношением E/p.

Следовательно, равновесие легче достигается при малой напряженности поля Е. повышенном давлении (малый пробег ) и высокой температуре газа.

Произведем оценку равновесия в столбе различных сварочных дуг.

Пример 1. Для W дуги в Ar P Па; = 2,5* ; E= 1* В/м; =3* м; ; kT 2 эВ, т.е. примерно 23000К. В результате получим

, т.е. около 5%

, т.е. около 2,5%

Вывод - термическое равновесие в столбе дуги существует.

Пример 2. Плазма вакуумной дуги: давление P=10 Па( 0,1 мм рт.ст); =50* и E= 1* В/м. Расчет дает это ведет к росту электронной температуры. Для прп ; ( ) и при T 5800К будет =0,5 эВ=0,8* . Для P= Па получим

т.е. пробег мал по сравнению с длиной дуги(несколько мм).

Для P=10 Па пробег увеличивается при T=const в раз и составляет =2* м = 20 мм. Т.е. пробег уже соизмерим с длиной дуги. Приняв условно 1,6* К, =15, получим

Вывод: В вакуумной дуге термического равновесия нет и электронная температура много больше температуры газа - в десятки раз.

В дугах низкого давления, а также в переходных зонах дуги, где E велико, отношение E/p велико, растет, термическое равновесие нарушается.

Общие свойства плазмы.

Всякое разделение зарядов приводит к возникновению электрических полей. Согласно законам электростатики при наличии на длине r см объемного заряда плотности q возникает электрическое поле, которое по уравнению Пуассона равно . Пусть в 1 имеется лишних электронов сверх тех, которые нейтрализуют заряд ионов. Тогда а E=4 *300*4,8* r 2* r. Для воздуха n=2,7* или примерно 5* атомов на 1 =5* в 1 .

Пример. Воздух в состоянии плазмы. Избыточная ионизация электронов =1%. Тогда n=5* . На длине r=1 см =1%. Тогда при =5* возникает поле E=2* r= В/см и объемная сила 72* Н/ . АПР расчетные силы в миллион раз больше наблюдаемых. Поэтому ясно, что в плотной плазме при = … при p Па. Распределение зарядов исчезающее мало и заметно лишь на очень малых расстояниях. Различают временное и приобретенное разделение зарядов.

Пространственное разделение измеряется дебаевским радиусом экранирования (поляризации) .

Энергия электрического поля при смещении электрона на расстояние r возникает за счет тепловой энергии электрона . Отсюда можно найти . Для разделения зарядов должно выполнятся неравенство ; .

Учитывая, что (уравнение Пуассона), а плотность объемного заряда q=en, то можно определить ионизацию “лишних” электронов сверх того количества, которое нейтрализует заряд ионов: (вап все электроны). Приняв r= и учитывая значение постоянных k, e, , получим после преобразований

[см]

Если размеры области занимаемой ионизированным газом с заданной концентрацией и электронной температурой значительно превосходят , то если есть многозарядные ионы с зарядом Z, то .

Это – условие квазинейтральности – основное условие, при соблюдении которого сложение заряженных частиц может называться плазмой

Пример. Для сварочной высокоионизированной плазмы при p= Па, T=10000К; = получим:

Вывод. В обычной дуге плазма квазинейтральна.

Пример. Сварка в вакууме при p= Па, T=160000К, =15 эВ=25* Дж;

мкм.

Вывод. При сварке в вакууме размер на 3 порядка меньше размеров столба дуги, поэтому и эту дугу можно считать все еще квазинейтральной

Плазма как идеальный газ

Идеальный газ – это система частиц, силами притяжения и радиусами которых можно пренебречь.

В сварочной плазме несмотря на сравнительно высокое давление P плотность частиц при высоких температурах дуги настолько мала, что возможно применение уравнений идеального газа, в том числе и закон газового состояния для 1 моля V=RT, который можно записать в виде P=nkT, где ; k=R/M; n=M/V; R=8,31 Дж/(моль*К) – универсальная газовая постоянная; N=6,02 * молекул/моль – число Авогадро.

Пример. При p= Па получаем n=p/(kT)=1,34* /(3* ) 2,7* =n. Это – число Лошмидта. В плазме дуги на воздухе при p= Па и T=6000К несмотря на ионизацию общее число частиц в 1 уменьшится почти в 20 раз – до

Для плазмы отступления от модели идеального газа при больших плотностях связаны с электрическим взаимодействием и вырождением.

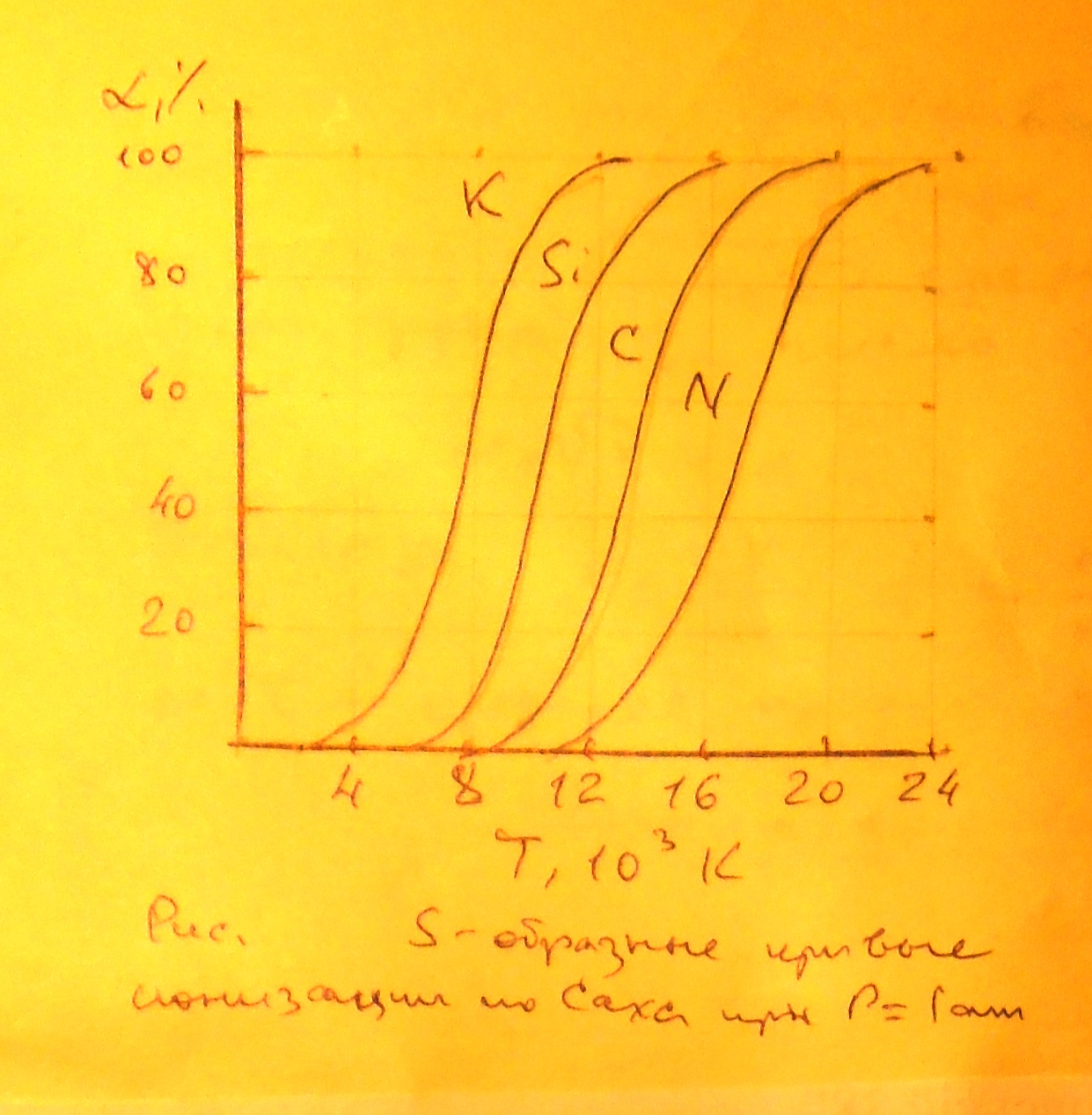
Уравнение Саха

В плазме, находящейся в термическом равновесии, температура всех частиц практически одинакова. Термическую ионизацию можно рассматривать как химическую реакцию газов:

работа ионизации

Степень ионизации = = . Из константы равновесия степень ионизации определяется уравнением Саха

где - квантовый коэффициент; , p, kT, e -степень ионизации газа, его давление, температура, энергия ионизации, g-статический (квантовый) вес, отвечающий числу возможных состояний частицы с одинаковой энергией. Для электрона =2, что соответствует двум направлениям спина. Для ионов и нейтральных атомов значения и вычисляют, исходя из строения атомов, значения для различных элементов вычислены Хреновым К.К.

ТАБЛИЦА

Иногда принимают . Тогда в уравнении Саха коэффициент 2.4 надо заменить на 3.2.

Уравнение Саха хорошо согласуется с экспериментом только при малых степенях ионизации, . При 6000К для натрия получим =0,21; для =0,23* .Следовательно, степень ионизации аргона по сравнению с ионизацией натрия при тех же температурах меньше в раз.

Кривые ионизации, построенные по уравнению Саха, имеют S-образный вид