Персептрон Розенблатта

Существуют различные методы построения линейных решающих правил. Рассмотрим один из них, реализованный в 50-х годах Розенблатом, в устройствах распознавания изображений, названных персептронами (рис. 5).

Пусть

если , , если ,

где  – некоторый объект одного из образов, .

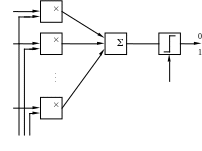
Рис. 5. Упрощённая схема однослойного персептрона

Выбор осуществляется пошаговым образом. Текущее значение заменяется новым после предъявления персептрону очередного объекта обучающей выборки. Эта корректировка производится по следующему правилу:

1.  , если и или если и .

2.  , если и , .

3.  , если и .

Это правило вполне логично. Если очередной объект системой классифицирован правильно, то нет оснований изменять . В случае (2) следует изменить так, чтобы увеличить . Предложенное правило удовлетворяет этому требованию. Действительно,

.

Соответственно в случае (3) .

Важное значение имеет выбор . Можно, в частности, выбрать . При этом показано, что если обучающие выборки двух образов линейно разделимы, то описанная пошаговая процедура сходится, то есть будут найдены значения , при которых

, если ,

, если .

Если же выборки линейно неразделимы, то сходимость отсутствует и оценку , минимизирующую число неправильных распознаваний, находят методом стохастической аппроксимации.

Обучение без учителя. Кластерный анализ. Группировка. Меры подобия. Итеративная оптимизация. Иерархическая группировка. Методы, основанные на теории графов. Группировка и уменьшение размерности. Метрическое шкалирование. Неметрическое шкалирование. Ранжирование. Качественные пространства.

Кластерный анализ

Кластерный анализ (самообучение, обучение без учителя, таксономия) применяется при автоматическом формировании перечня образов по обучающей выборке. Все объекты этой выборки предъявляются системе без указания, какому классу они принадлежат. Подобного рода задачи решает, например, человек в процессе естественно-научного познания окружающего мира (классификации растений, животных).

В основе кластерного анализа лежит гипотеза компактности. Предполагается, что обучающая выборка в признаковом пространстве состоит из набора сгустков (подобно галактикам во Вселенной). Задача системы – выявить и формализовано описать эти сгустки. Геометрическая интерпретация гипотезы компактности состоит в том, что объекты, относящиеся к одному таксону, расположены близко друг к другу по сравнению с объектами, относящимися к разным таксонам.

При всей своей наглядности и интерпретируемости результатов кластеризации, даже в двумерном случае возникают неоднозначные ситуации при образовании кластеров различного размера и различной плотности (рис.14).

Рис. 14. Иерархическая (двухуровневая) таксономия

Факторы, определяющие "хорошую" кластеризацию, можно сформулировать следующим образом:

– внутри кластеров объекты должны быть как можно ближе друг к другу (обобщённый показатель );

– кластеры должны как можно дальше отстоять друг от друга (обобщённый показатель );

– в кластерах количество объектов должно быть по возможности одинаковым, то есть их различие в разных кластерах нужно минимизировать (обобщённый показатель );

– внутри кластеров не должно быть больших скачков плотности точек, то есть количества точек на единицу объёма (обобщённый показатель ).

Если удается удачно подобрать способы измерения и то можно добиться хорошего совпадения "человеческой" и автоматической кластеризации.

Термин кластерный анализ (впервые ввел Tryon, 1939) в действительности включает в себя набор различных алгоритмов классификации. Общий вопрос, задаваемый исследователями во многих областях, состоит в том, как организовать наблюдаемые данные в наглядные структуры, т.е. развернуть таксономии. Например, биологи ставят цель разбить животных на различные виды, чтобы содержательно описать различия между ними. В соответствии с современной системой, принятой в биологии, человек принадлежит к приматам, млекопитающим, амниотам, позвоночным и животным. Заметьте, что в этой классификации, чем выше уровень агрегации, тем меньше сходства между членами в соответствующем классе. Человек имеет больше сходства с другими приматами (т.е. с обезьянами), чем с "отдаленными" членами семейства млекопитающих (например, собаками) и т.д. В последующих разделах будут рассмотрены общие методы кластерного анализа, см. Объединение (древовидная кластеризация) и Метод K средних.

Техника кластеризации применяется в самых разнообразных областях. Хартиган (Hartigan, 1975) дал прекрасный обзор многих опубликованных исследований, содержащих результаты, полученные методами кластерного анализа. Например, в области медицины кластеризация заболеваний, лечения заболеваний или симптомов заболеваний приводит к широко используемым таксономиям. В области психиатрии правильная диагностика кластеров симптомов, таких как паранойя, шизофрения и т.д., является решающей для успешной терапии. В археологии с помощью кластерного анализа исследователи пытаются установить таксономии каменных орудий, похоронных объектов и т.д. Известны широкие применения кластерного анализа в маркетинговых исследованиях. В общем, всякий раз, когда необходимо классифицировать "горы" информации к пригодным для дальнейшей обработки группам, кластерный анализ оказывается весьма полезным и эффективным.

Объединение (древовидная кластеризация)

Назначение этого алгоритма состоит в объединении объектов (например, животных) в достаточно большие кластеры, используя некоторую меру сходства или расстояние между объектами. Типичным результатом такой кластеризации является иерархическое дерево.

Иерархическое дерево

Рассмотрим горизонтальную древовидную диаграмму. Диаграмма начинается с каждого объекта в классе (в левой части диаграммы). Теперь представим себе, что постепенно (очень малыми шагами) вы "ослабляете" ваш критерий о том, какие объекты являются уникальными, а какие нет. Другими словами, вы понижаете порог, относящийся к решению об объединении двух или более объектов в один кластер.

В результате, вы связываете вместе всё большее и большее число объектов и агрегируете (объединяете) все больше и больше кластеров, состоящих из все сильнее различающихся элементов. Окончательно, на последнем шаге все объекты объединяются вместе. На этих диаграммах горизонтальные оси представляют расстояние объединения (в вертикальных древовидных диаграммах вертикальные оси представляют расстояние объединения). Так, для каждого узла в графе (там, где формируется новый кластер) вы можете видеть величину расстояния, для которого соответствующие элементы связываются в новый единственный кластер. Когда данные имеют ясную "структуру" в терминах кластеров объектов, сходных между собой, тогда эта структура, скорее всего, должна быть отражена в иерархическом дереве различными ветвями. В результате успешного анализа методом объединения появляется возможность обнаружить кластеры (ветви) и интерпретировать их.

Меры расстояния

Объединение или метод древовидной кластеризации используется при формировании кластеров несходства или расстояния между объектами. Эти расстояния могут определяться в одномерном или многомерном пространстве. Например, если вы должны кластеризовать типы еды в кафе, то можете принять во внимание количество содержащихся в ней калорий, цену, субъективную оценку вкуса и т.д. Наиболее прямой путь вычисления расстояний между объектами в многомерном пространстве состоит в вычислении евклидовых расстояний. Если вы имеете двух- или трёхмерное пространство, то эта мера является реальным геометрическим расстоянием между объектами в пространстве (как будто расстояния между объектами измерены рулеткой). Однако алгоритм объединения не "заботится" о том, являются ли "предоставленные" для этого расстояния настоящими или некоторыми другими производными мерами расстояния, что более значимо для исследователя; и задачей исследователей является подобрать правильный метод для специфических применений.

Евклидово расстояние. Это, по-видимому, наиболее общий тип расстояния. Оно попросту является геометрическим расстоянием в многомерном пространстве и вычисляется следующим образом:

расстояние(x,y) = { _i (x_i - y_i)² }^1/2

Заметим, что евклидово расстояние (и его квадрат) вычисляется по исходным, а не по стандартизованным данным. Это обычный способ его вычисления, который имеет определенные преимущества (например, расстояние между двумя объектами не изменяется при введении в анализ нового объекта, который может оказаться выбросом). Тем не менее, на расстояния могут сильно влиять различия между осями, по координатам которых вычисляются эти расстояния. К примеру, если одна из осей измерена в сантиметрах, а вы потом переведете ее в миллиметры (умножая значения на 10), то окончательное евклидово расстояние (или квадрат евклидова расстояния), вычисляемое по координатам, сильно изменится, и, как следствие, результаты кластерного анализа могут сильно отличаться от предыдущих.

Квадрат евклидова расстояния. Иногда может возникнуть желание возвести в квадрат стандартное евклидово расстояние, чтобы придать большие веса более отдаленным друг от друга объектам. Это расстояние вычисляется следующим образом (см. также замечания в предыдущем пункте):

расстояние(x,y) = _i (x_i - y_i)²

Расстояние городских кварталов (манхэттенское расстояние). Это расстояние является просто средним разностей по координатам. В большинстве случаев эта мера расстояния приводит к таким же результатам, как и для обычного расстояния Евклида. Однако отметим, что для этой меры влияние отдельных больших разностей (выбросов) уменьшается (так как они не возводятся в квадрат). Манхэттенское расстояние вычисляется по формуле:

расстояние(x,y) = _i |x_i - y_i|

Расстояние Чебышева. Это расстояние может оказаться полезным, когда желают определить два объекта как "различные", если они различаются по какой-либо одной координате (каким-либо одним измерением). Расстояние Чебышева вычисляется по формуле:

расстояние(x,y) = Максимум|x_i - y_i|

Степенное расстояние. Иногда желают прогрессивно увеличить или уменьшить вес, относящийся к размерности, для которой соответствующие объекты сильно отличаются. Это может быть достигнуто с использованием степенного расстояния. Степенное расстояние вычисляется по формуле:

расстояние(x,y) = ( _i |x_i - y_i|^p)^1/r

где r и p - параметры, определяемые пользователем. Несколько примеров вычислений могут показать, как "работает" эта мера. Параметр p ответственен за постепенное взвешивание разностей по отдельным координатам, параметр r ответственен за прогрессивное взвешивание больших расстояний между объектами. Если оба параметра - r и p, равны двум, то это расстояние совпадает с расстоянием Евклида.

Процент несогласия. Эта мера используется в тех случаях, когда данные являются категориальными. Это расстояние вычисляется по формуле:

расстояние(x,y) = (Количество x_i y_i)/ i

Правила объединения или связи

На первом шаге, когда каждый объект представляет собой отдельный кластер, расстояния между этими объектами определяются выбранной мерой. Однако когда связываются вместе несколько объектов, возникает вопрос, как следует определить расстояния между кластерами? Другими словами, необходимо правило объединения или связи для двух кластеров. Здесь имеются различные возможности: например, вы можете связать два кластера вместе, когда любые два объекта в двух кластерах ближе друг к другу, чем соответствующее расстояние связи. Другими словами, вы используете "правило ближайшего соседа" для определения расстояния между кластерами; этот метод называется методом одиночной связи. Это правило строит "волокнистые" кластеры, т.е. кластеры, "сцепленные вместе" только отдельными элементами, случайно оказавшимися ближе остальных друг к другу. Как альтернативу вы можете использовать соседей в кластерах, которые находятся дальше всех остальных пар объектов друг от друга. Этот метод называется метод полной связи. Существует также множество других методов объединения кластеров, подобных тем, что были рассмотрены.

Одиночная связь (метод ближайшего соседа). Как было описано выше, в этом методе расстояние между двумя кластерами определяется расстоянием между двумя наиболее близкими объектами (ближайшими соседями) в различных кластерах. Это правило должно, в известном смысле, нанизывать объекты вместе для формирования кластеров, и результирующие кластеры имеют тенденцию быть представленными длинными "цепочками".

Полная связь (метод наиболее удаленных соседей). В этом методе расстояния между кластерами определяются наибольшим расстоянием между любыми двумя объектами в различных кластерах (т.е. "наиболее удаленными соседями"). Этот метод обычно работает очень хорошо, когда объекты происходят на самом деле из реально различных "рощ". Если же кластеры имеют в некотором роде удлиненную форму или их естественный тип является "цепочечным", то этот метод непригоден.

Невзвешенное попарное среднее. В этом методе расстояние между двумя различными кластерами вычисляется как среднее расстояние между всеми парами объектов в них. Метод эффективен, когда объекты в действительности формируют различные "рощи", однако он работает одинаково хорошо и в случаях протяженных ("цепочного" типа) кластеров. Отметим, что в своей книге Снит и Сокэл (Sneath, Sokal, 1973) вводят аббревиатуру UPGMA для ссылки на этот метод, как на метод невзвешенного попарного арифметического среднего - unweighted pair-group method using arithmetic averages.

Взвешенное попарное среднее. Метод идентичен методу невзвешенного попарного среднего, за исключением того, что при вычислениях размер соответствующих кластеров (т.е. число объектов, содержащихся в них) используется в качестве весового коэффициента. Поэтому предлагаемый метод должен быть использован (скорее даже, чем предыдущий), когда предполагаются неравные размеры кластеров. В книге Снита и Сокэла (Sneath, Sokal, 1973) вводится аббревиатура WPGMA для ссылки на этот метод, как на метод взвешенного попарного арифметического среднего - weighted pair-group method using arithmetic averages.

Невзвешенный центроидный метод. В этом методе расстояние между двумя кластерами определяется как расстояние между их центрами тяжести. Снит и Сокэл (Sneath and Sokal (1973)) используют аббревиатуру UPGMC для ссылки на этот метод, как на метод невзвешенного попарного центроидного усреднения - unweighted pair-group method using the centroid average.

Взвешенный центроидный метод (медиана). тот метод идентичен предыдущему, за исключением того, что при вычислениях используются веса для учёта разницы между размерами кластеров (т.е. числами объектов в них). Поэтому, если имеются (или подозреваются) значительные отличия в размерах кластеров, этот метод оказывается предпочтительнее предыдущего. Снит и Сокэл (Sneath, Sokal 1973) использовали аббревиатуру WPGMC для ссылок на него, как на метод невзвешенного попарного центроидного усреднения - weighted pair-group method using the centroid average.

Метод Варда. Этот метод отличается от всех других методов, поскольку он использует методы дисперсионного анализа для оценки расстояний между кластерами. Метод минимизирует сумму квадратов (SS) для любых двух (гипотетических) кластеров, которые могут быть сформированы на каждом шаге. Подробности можно найти в работе Варда (Ward, 1963). В целом метод представляется очень эффективным, однако он стремится создавать кластеры малого размера.

Метод K средних

Этот метод кластеризации существенно отличается от таких агломеративных методов, как древовидная кластеризация. Предположим, вы уже имеете гипотезы относительно числа кластеров (по наблюдениям или по переменным). Вы можете указать системе образовать ровно три кластера так, чтобы они были настолько различны, насколько это возможно. Это именно тот тип задач, которые решает алгоритм метода K средних. В общем случае метод K средних строит ровно K различных кластеров, расположенных на возможно больших расстояниях друг от друга.

Базовый алгоритм кластеризации k-средними достаточно прост: Дано заданное пользователем фиксированное число кластеров k, перемещайте наблюдения в кластере для максимизации расстояния между центрами кластеров; центры кластеров обычно определяются вектором средних значений для всех (непрерывных) переменных в анализе.

Возможны следующие расширения и обобщения данного метода:

1. Вместо того чтобы задавать соответствие наблюдений кластерам так, чтобы максимизировать разницу в средних для непрерывных переменных, алгоритм кластеризации EM (поиск максимума) вычисляет вероятности членства в кластере, основываясь на одном или более вероятностном распределении. Цель алгоритма кластеризации - максимизировать вероятность полного правдоподобия данных, задаваемых в (последних) кластерах.

2. В отличие от классической реализации алгоритма кластеризации k-средними, алгоритмы обобщенных k-средних и EM могут быть применены равно для непрерывных и категориальных переменных.

3. Основное отличие алгоритма кластеризации k-средними в том, что вы должны указать число кластеров перед началом анализа (то есть, число кластеров должно быть априори известно); в обобщенном случае используется измененная схема v-кратной кросс-проверки для определения наилучшего числа кластеров по данным.

Алгоритм К-средних

Алгоритм К-средних является методом кластеризации, используемый для разделения набора объектов на k групп в соответствии с указанной мерой близости. Основной алгоритм разделен на два шага.

1. Вычисление центроидов кластера

a. Начальные центроиды устанавливаются, используя метод, указанный пользователем. Три метода начальных центров: выбрать N наблюдений для максимизации начального расстояния, случайно выбрать N наблюдений, и выбрать первые N наблюдений. Здесь N означает k.

b. После присвоения всех объектов ближайшему центроиду, вычисляются новые центроиды, используя все члены им присвоенные. Для непрерывных переменных значение центроида есть среднее значений всех членов, присвоенных этому кластеру. Для категориальных переменных значение центроида есть первая модель всех членов ему присвоенных.

2. Присвоение каждого объекта ближайшему центроиду

a. Ближайший центроид в точности использует метод заданной меры близости. Значения всех непрерывных переменных перед вычислением нормализуются. Отметьте, что c обозначает центроид и x обозначает наблюдение.

i. Если i-я переменная категориальная, (xi - ci) равно 0 если их значения совпадают, иначе равно 1.

ii. Если i-я переменная непрерывна, xi и ci сперва нормализуются, используя минимальное и максимальное значения этих переменных.

Евклидово расстояние:

distance( x,  c ) = {еi (xi - ci)2 }Ѕ

Квадрат евклидова расстояния:

distance( x,  c ) = еi (xi - ci)2

Манхэттенское расстояние:

distance( x,  c ) = еi |xi - ci|

Расстояния Чебышева:

distance( x,  c ) = Maximum|xi - ci|

b. Если все наблюдения принадлежат кластеру, которому принадлежали до текущей итерации, прервите итерацию. Также, если число итераций равно максимальному числу итераций, прервите итерацию. Обновите центроиды и получите окончательную кластеризацию.

Многомерное шкалирование

Многомерное шкалирование (МШ) - одно из направлений анализа данных; оно отличается от других методов МСА, прежде всего видом исходных данных, которые в данном случав представляют собой матрицу близости между парами объектов (“близость”, или "сходство", объектов можно определять различными способами). Цель МШ - это описание матрицы близости в терминах расстояний между точками, представление данных о сходстве объектов в виде системы точек в пространстве малой размерности (например, на двумерной плоскости). Упрощая, можно сказать, что 'на вход' методов МШ подается матрица близости, а "на выходе" получается координатное раз смещение точек.

Основное предположение МШ заключается в том, что существует некоторое метрическое пространство существенных базовых характеристик, которые неявно и послужили основой для полученных эмпирических данных о близости между парами объектов. Следовательно, объекты можно представить как точки в этом пространстве. Предполагают также, что более близким (по исходной матрице) объектам соответствуют меньшие расстояния в пространстве базовых характеристик. Таким образом, многомерное шкалирование - это совокупность методов анализа эмпирических данных о близости объектов, с помощью которых определяется размерность пространства существенных для данной содержательной задачи характеристик измеряемых объектов и конструируется конфигурация точек (объектов) в этом пространстве. Это пространство ('многомерная шкала') аналогично обычно используемым шкалам в том смысле, что значениям существенных характеристик измеряемых объектов соответствуют определенные позиции на осях пространства.

Данные в исходной матрице близости объектов могут быть получены различными способами. Вообще говоря, методы МШ ориентируются на экспертные оценки близости объектов, когда респонденту предъявляют пары объектов, и он должен упорядочить их по степени внутреннего сходства, которое иногда оценивается в баллах. Если данные о близости пар объектов не получены непосредственно, а рассчитаны на основании других данных (различные коэффициенты связи), то следует иметь в виду, что МШ может оказаться далеко не лучшим способом анализа структуры исходных данных. Действительно, первичные данные, на основе которых рассчитывались близости, содержат больше информации, чем 'вторичные' данные о близости. Матрица близости должна удовлетворять определенным естественным условиям.

Методы МШ делятся обычно на две категории: неметрическое МШ (НМШ) и метрическое МШ (ММЩ). Методы ММШ используют, когда оценки близости получены на количественной шкале (не ниже интервальной). В таком виде в исследованиях социальных проблем оценки близости возникают крайне редко. Более естественной является оценка близости, измеренная на порядковой шкале (когда пары объектов можно только упорядочить по степени схожести объектов). В этом случае используют методы НМШ, которые дают "покоординатную развертку" матрицы близости в пространстве двух-трех существенных характеристик, так что упорядочения объектов по матрице близости расстояниям в этом пространстве совпадают.

Основные возможности методов многомерного шкалирования:

1. Построение метрического пространства невысокой размерности, в котором наилучшим образом сохраняется структура исходных данных о близости пар объектов. Проектирование объектов на оси полученного пространства определяет их положение на этих осях, т.е. производится процесс шкалирования.

2. Визуализация структуры исходных данных в виде кон фигурации точек (объектов) в двух-трехмерном базовом пространстве.

3. Интерпретация полученных осей (базовых характеристик) и конфигурации объектов - конечный результат применения МШ, дающий новое знание об изучаемой структуре (в случае корректного использования метода на всех этапах).

Характер конфигурации объектов, а также 'внешние' по отношению к исходным данным сведения позволяют дать содержательную интерпретацию осям и тем самым выявить 'глубинные' мотивы, которыми руководствовались эксперты, упорядочивая пары объектов по степени их близости (в одном случае), или обнаружить 'скрытые' факторы, определяющие структуру сходства и различия объектов (в другом случае).

Для повышения достоверности получаемых с помощью методов МШ результатов в одном исследовании нередко используют разные методы МШ; кроме того, эти методы применяют совместно с другими методами МСА; кластер-анализом, факторным анализом, множественной регрессией.

Логическое программирование и экспертные системы (ЭС). Логические модели. Логический вывод. Логическое программирование. Правила продукции. Обратный логический вывод. Экспертные системы.

Байесовское объединение свидетельств. Оценка достоверности выводов. Вероятностно-логический вывод. Нечеткая логика. Объединение свидетельств по схеме Демпстера-Шафера. Практический пример: диагностика в медицине.

Формула Байеса

Теорема  (формула Байеса). Пусть — полная группа событий, и — некоторое событие, вероятность которого положительна. Тогда условная вероятность того, что имело место событие , если в результате эксперимента наблюдалось событие , может быть вычислена по формуле:

Доказательство. По определению условной вероятности,

QED

Анализ свидетельств

Пусть дан набор попарно независимых гипотез A, составляющих полную группу событий, и наблюдается некоторое событие B. Как известно, в этом случае формула Байеса имеет вид:

P(A_i/B)=[P(A_i)P(B/A_i)]/[{P(A_i)P(B/A_i)}].

Пусть теперь наблюдается изображение Im, и необходимо определить апостериорную вероятность некоторой гипотезы H относительно видимой сцены. Тогда формула Байеса принимает вид

P(H/Im)=[P(H)P(Im/H)]/[P(H)P(Im/H)+P(H^С)P(Im/H^С)], (*.7)

где H^С - гипотеза "не H"; под событием (event) E(H) подразумевается событие "H - истинно".

Изображение Im здесь также рассматривается как событие или, точнее, должно рассматриваться событие E(Im), связанное с данным изображением. Далее будем считать, что в процессе анализа изображения Im происходит ряд событий, совокупность которых и составляет E(Im). Иными словами, если каждый существенный факт, установленный в ходе анализа изображения Im, есть событие e_k, то

E(Im)=e₁e₂..e_K, (*.8)

где K - общее число таких событий. Таким образом, для проверки любой гипотезы H относительно изображения Im необходимо вычислить выражение (7) с учетом (8).

Если предположить, что события {e_k} независимы в совокупности, то из (.7) и (.8) следует

P(H/Im)=[P(H){P(e_k/H)}]/[P(H){P(e_k/H)}+P(H^С){P(e_k/H^С)}], (.7’)

где {x_k}=x₁x₂...x_K.

Выражение (7’) дает возможность определить важное понятие "влияющего события" или "свидетельства". Пусть даны некоторое событие e и некотрая гипотеза H, причем P(e/H)=P(e/H^C). Тогда из (.7’) следует, что

(P(e/H)=P(e/H^C))(P(H/{Im\e})=P(H/{Ime})),

иными словами, наличие или отсутствие события e никак не влияет на апостериорную вероятность гипотезы H. Таким образом

Определение.1. Любое событие e, такое что P(e/H)(P(e/H^C) является влияющим событием для гипотезы H.

В дальнейшем без потери общности будем считать, что произведение в формуле (.7’) берется не по всем событиям вообще, а только по совокупности влияющих событий для каждой исследуемой гипотезы.

Определение.2. Событийной вероятностной моделью изображения объекта называется набор PE(H)={{p(e_k/H),p(e_k/H^C),e_kE(Im)}, p(H)}, где Im - изображение, H - гипотеза о присутствии некоторого объекта на изображении, H^C - ее дополнение; E(Im)={e_k} - множество влияющих событий относительно гипотезы H, регистрируемых на данном изображении Im.

Вообще говоря, переход от изображения, представленного в виде дискретного двумерного числового поля Im={Im_xy}, x=1..DimX, y=1..DimY, Im_xy[0..2N-1] к представлению в виде множества событий E(Im)={e_k} не является ни очевидным ни даже обоснованным. Попробуем его обосновать.

Пусть известна вероятностная модель изображения объекта PM(H)={p(Im/H), p(Im/H^C), p(H)}. И пусть решение об обнаружении объекта принимается на основании значения апостериорной вероятности P(H/Im) в соответствии с выражением (.7). Пусть дан также набор событий E(Im)={e_k}=func(Im), характеризуемый соответственно событийной моделью PE(H)={p(E(Im)/H), p(E(Im)/H^C), p(H)}. При каких условиях решения, принятые на основании модели PE(H), будут в точности равны решениям, принятым на основании модели PM(H)? Очевидно, в том случае, когда

P(H/Im)=P(H/E(Im)), (.9)

то есть выражения (.7) и (.7’) дают одинаковый результат.

Определение.3. Пусть u и v - два описания изображения, причем u=u(v) - некоторая функция от v. Пусть также некоторый параметр x принимает свои значения на соответствующем множестве. Тогда u называется достаточной статистикой для v относительно параметра x или семейства распределений {p(v/x): xX}, если условная плотность p(v/u,x) не зависит от х.

В работе [1] доказано следующее достаточное условие достаточности статистики при проверке альтернативных гипотез:

Утверждение 1. Пусть u и v - два описания изображения, причем u=u(v). Пусть также дан некоторый набор альтернативных гипотез H={H_i:H_iH_j=}, составляющих полную группу событий. Тогда u будет достаточной статистикой для v относительно гипотез из H или семейства распределений {p(v/H_i): H_iH}, если справедливо равенство P(H_i/v)=P(H_i/u) для всех H_iH.

Определение.4. Пусть u и v - два описания изображения, причем u=u(v). Пусть H={H,H^C} - набор альтернативных гипотез, составляющих полную группу событий. Тогда вероятностные модели P(v,H)={p(v/H),p(v/H^C),p(H)} и P(u,H)={p(u/H),p(u/H^C),p(H)}, связанные условием

P(H/v)=P(H/u)

будем называть адекватными относительно H.

Таким образом из введенных определений, утверждения 1 и условия (.9) следует, что переход от описания Im к описанию E(Im) является обоснованным только в том случе, когда E(Im) является достаточной статистикой для Im относительно гипотезы H. Только при этом условии вероятностные модели PE(H) и PM(H) будут адекватными.

Дадим следующую семантическую интерпретацию условию достаточности статистики вида “p(v/u,x) не зависит от х”. Пусть под множеством событий E(Im) понимается совокупность контурных точек вместе с их координатами, и гипотеза H_i состоит в том, что на изображении находится объект некоторой i-й формы. Конкретные значения пикселов зависят, очевидно, от условий регистрации (освещенность + параметры камеры), между тем, контурный препарат является инвариантным к этим условиям носителем искомой информации. В этом случае действительно при любом объекте H_i справедливо равенство p(Im/E(Im),H_i) =p(Im/E(Im)), где p(Im/E(Im)) - вероятность некоторой полутоновой “раскраски” контурного изображения, описывающая условия регистрации изображения, никак не зависящие от характера наблюдаемого объекта.

Полезным с практической точки зрения представляется также ввести следующее понятие:

Определение.5. Пусть u и v - два описания изображения, причем u=u(v). Пусть H={H,H^C} - набор альтернативных гипотез, составляющих полную группу событий. Тогда вероятностная модель P(u,H)={p(u/H),p(u/H^C),p(H)} называется загрублением модели P(v,H)={p(v/H),p(v/H^C),p(H)}, если P(H/v)(P(H/u).

Использование загрубленных моделей может быть полезно на предварительном этапе тестирования гипотез, когда необходимо обеспечить только отсутствие ошибок второго рода (т.е. пропусков), и предполагается что ошибки первого рода (ложные обнаружения) будут отбракованы в дальнейшем.

Так или иначе, далее под обозначением P(H/Im) мы будем всегда понимать P(H/E(Im)), где E(Im) - событийное описание изображения.