Выделение отличий изображений по форме

Пусть форма изображения задана в виде оператора ортогонального проецирования на и предъявляется некоторое изображение . Требуется указать, в чем состоит отличие по форме изображения от . Так как изображение является наилучшим приближением изображениями, сравнимыми по форме с , то изображение представляет все то, что отличает от по форме.

Иллюстрация эффективности такого способа выделения отличий по форме представлена на рис. 6.2.2. На рис. 6.2.7 приведен еще один пример выделения отличий по форме. Предъявлены изображения двух сцен, приведенные на рис.7 вверху, полученные при различных условиях регистрации, требуется найти различие в сценах. Изображение слева внизу показывает отличие в яркостях предъявленных изображений и не дает возможности заметить отличие в сценах, морфологическая разность , приведенная на рис. 6.2.7 справа внизу выделяет область поля зрения, на которой изображен объект, отсутствующий на исходной сцене.

Обнаружение объекта по его изображению и оценка его координат

На практике большой интерес представляют задачи совмещения и выделения фрагментов заданной формы на предъявленном изображении. Пример такой задачи приведен во введении. Как известно, если отличие яркостей сравниваемых по форме фрагментов не сводится к однородному изменению их яркости и контраста, то в таких задачах широко распространенные корреляционные методы работают недостаточно эффективно.

Пусть дано изображение , причем на подмножестве поля зрения имеется фрагмент , форма которого рассматривается как эталон формы. Напомним, что функция равна нулю вне множества , и равна единице на множестве ; таким образом, яркость изображения равна яркости изображения на множестве и равна нулю вне . Рассмотрим группу преобразований плоскости , и – множество преобразований из , таких, что полностью содержится в области , если . Следует найти такое преобразование , чтобы фрагмент изображения на подмножестве был близок по форме к фрагменту изображения на подмножестве . Опишем эту задачу как рассмотренную выше задачу сравнения формы двух изображений, заданных на поле зрения .

Определим меру близости указанных фрагментов по форме. Назовем формой фрагмента изображения на подмножестве множество изображений, форма которых не сложнее, чем форма любого изображения вида , где – произвольное изображение. Иными словами, форма изображения на определяется как множество изображений, яркость которых на может быть получена преобразованиями изображения вида , где пробегает по всему множеству , а на дополнении к (на фоне) яркость изображения произвольна. Проектор на это множество обозначим .

Фрагмент заданной формы на предъявленном для анализа изображении будет обнаружен, если = , где - проектор на множество . Для определения близости фрагментов по форме обозначим проектор на множество изображений, форма которых не сложнее чем форма любого из изображений вида , где – произвольное изображение. Иными словами, - проектор на множество изображений, яркость которых равных константе на подмножестве и произвольна вне его. Тогда близость фрагмента предъявленного изображения к форме фрагмента изображения на подмножестве определим значением дроби .

Если на изображении фрагмент заданной формы расположен на подмножестве , то сравнивать по форме на подмножестве следует фрагменты изображений и , где

Близость фрагмента изображения на множестве к форме фрагмента изображения на множестве определим значением дроби .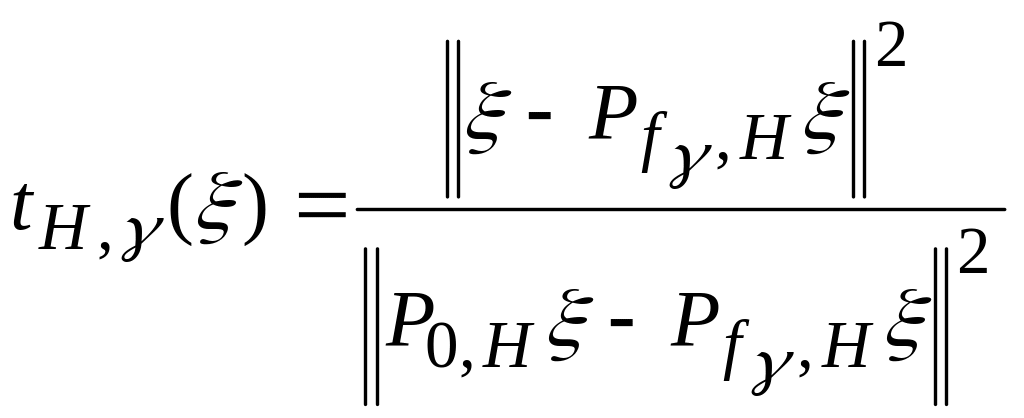

Пусть - группа сдвигов плоскости , так, что при задании декартовых прямоугольных координат любой вектор преобразование превращает в вектор . На рис. 6.2.4 приведены значения , обратные близости фрагментов по форме, в зависимости от координат вектора сдвига. Максимальное значение величины определяет координаты вектора сдвига плоскости, совмещающие близкие по форме фрагменты изображений и .