Бинаризация полутоновых изображений

В обработке изображений часто используется процедура «пороговой бинаризации» – разбиение изображения на две области, одна из которых содержит все пиксели со значением ниже некоторого порога, а другая содержит все пиксели со значением выше этого порога.

Алгоритмы адаптивной бинаризации изображений базируются на использовании локальной или глобальной гистограммы изображения [20]. Подход, основанный на использовании гистограммы яркостей пикселей, является одним из самых известных и, безусловно, наиболее простым.

Оптимальная пороговая сегментация основана на приближении гистограммы изображения к некоторой кривой, используя весовые суммы двух или более вероятностей интенсивности с нормальным распределением. Тогда порог – это набор ближайших уровней яркости, соответствующих минимуму вероятности между максимумами двух или более нормальных распределений.

@Рис. 3.1.1. Уровни яркости гистограммы аппроксимируются двумя нормальными распределениями. (а) Функции распределения объекта и фона. (б) Соответствующие гистограммы и оптимальный порог

Для определения оптимального порога бинаризации предложено большое количество различных подходов. Наиболее удачным из них представляется подход Otsu [230], который предполагает не только определение оптимального порога бинаризации, но и вычисление некоторого критерия бимодальности, то есть оценку того, действительно ли исследуемая гистограмма содержит именно две моды (два выраженных пика). Идея данного подхода заключается в следующем.

Пусть изображение представляет собой двумерный массив IM размера XY, причем его элементы (пиксели) принимают значения на отрезке [0..255]. Тогда гистограмма этого изображения представляет собой одномерный массив Hist[0..255], в каждой ячейке которого Hist[i] содержится число пикселей изображения, имеющих значение, равное i. Рассмотрим теперь «подгистограмму» Hist[k...l], 0k, l255. Для любой такой подгистограммы (окна) [k,l] можно вычислить оценку математического ожидания яркости пикселей MO(k,l) и оценку дисперсии DISP(k,l). Пусть дан порог t: 0t255.

Тогда для данного порога t можно вычислить «критерий разделимости» SC вида

SC(t) = 1 – (DISP(0,t) + DISP(t+1,255)) / DISP(0,255) (3.1.1)

Критерий SC(t) всегда принимает значение на отрезке [0,1], причем значение его тем больше, чем лучше разделимость яркостного распределения на два класса относительно порога t. Алгоритм Отсу предполагает вычисление SC(t) для всех t[0..255], после чего оптимальный порог Отсу определяется как

T = argmax SC(t), t[0..255] (3.1.2).

Этот алгоритм имеет ясный статистический смысл и, как показывает практика, является эффективным и устойчивым способом определения адаптивного порога для бинаризации бимодальных изображений.

Сегментация многомодальных изображений

Специально разработанный для данного класса задач, метод статистического выделения мод позволяет оценивать количество и степень выраженности мод гистограммы, опираясь на соответствующий график статистической производной (функции локальной разделимости), представляющий собой график значений критерия Отсу, вычисляемых в локальном скользящем окне, согласованном по ширине с ожидаемой шириной моды гистограммы (рис. 3.1.2).

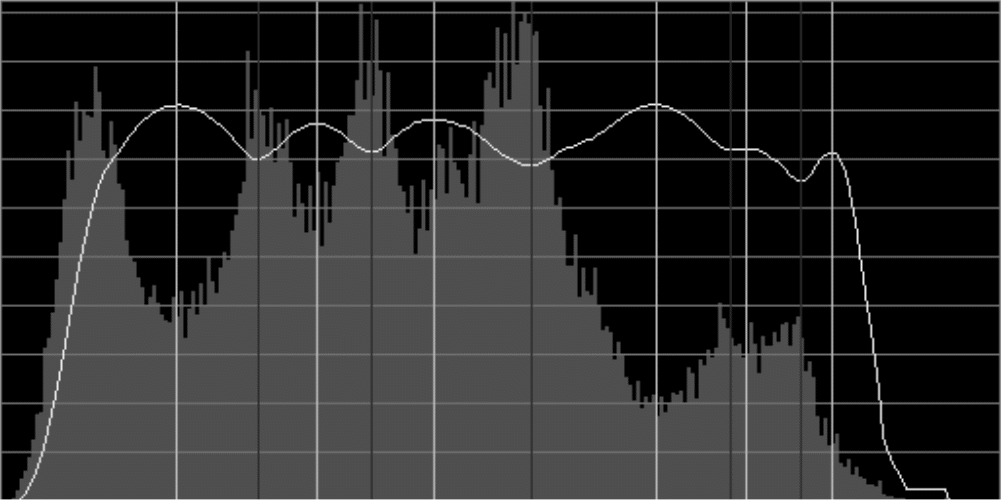
@Рис. 3.1.2. Пример автоматического разделения мод на гистограмме по максимумам функции локальной разделимости

Другой способ автоматического выделения мод гистограммы основывается на непосредственной оптимизации глобального критерия разделимости на n>1 мод, подобного критерию бимодальной разделимости Отсу. Введем (n+1)-мерный вектор t=(t₀,..t_n), где t₀=0, t_n=255, t₁,..t_n-1 - свободные переменные, соответствующие порогам, разделяющим моды гистограммы. Тогда среднеквадратичный критерий оптимального выбора порогов сегментации будет иметь следующий вид:

_i=0,..,n DISP(t_i, t_i+1)  min(t₁,..t_n-1).

Поскольку гистограмма – одномерный массив, эта задача однозначно решается методом динамического программирования [5]. В результате определяется такой набор порогов сегментации, который обеспечивает минимальное среднеквадратичное отклонение сегментированного на n уровней изображения от исходного.

На рис. 3.1.3. приводится пример автоматической гистограммной сегментации изображения при автоматическом оптимальном выделении набора порогов при заданном оптимальном числе мод гистограммы.

Если число мод гистограммы заранее неизвестно, то задача гистограммной сегментации является, вообще говоря, некорректной по Адамару и требует регуляризации [42]. В качестве регуляризованного критерия можно применить, например, следующий критерий, одновременно штрафующий и суммарное среднеквадратичное отклонение сегментированного изображения от исходного, и число выделяемых при сегментации мод:

_i=0,..,n DISP(t_i, t_i+1) + n  min(n,t₁,..t_n-1).

При фиксированном значении регуляризирующего параметра  соответствующая процедура динамического программирования автоматически определяет оптимальное число мод n и одновременно – соответствующий оптимальный набор порогов. Однако выбор регуляризирующего параметра  также является некой эвристической процедурой, и потому в практических задачах проще оказывается выбирать число мод гистограммы.

а) б)

в) г)

@Рис. 3.1.3. Пример автоматической гистограммной сегментации изображения: а) при выделении 10 мод гистограммы; б) при выделении 5 мод гистограммы; в) при выделении 3 мод гистограммы; г) при выделении 2 мод гистограммы.