Задача 4.

Заряды = 1 мкКл и =2 мкКл находятся на серединах соседних сторон квадрата со стороной = 1 м и создают электрическое поле с напряженностью в точке Р, находящейся в вершине квадрата (см. рис. 2). Найти величину горизонтальной и вертикальной проекции вектора , а также его модуль

Решение:

Проведем оси х и у вдоль двух сторон квадрата, а начало отсчета поместим в точку Р. Расстояния от зарядов и до точки Р равны м,

м.

Можно найти косинус и синус угла :

;

Воспользуемся формулами (3.4) и (3.5), а затем и (3.7):

кВ/м

6,43 кВ/м

кВ/м

Модуль вектора можно найти с помощью формулы (3.3), не находя его проекции:

Ответ: кВ/м; 6,43 кВ/м;

3.1 З аряд находится в вершине квадрата со стороной , а заряд – в центре. Найти модуль напряженности электрического поля в точке Р, находящейся в другой вершине этого квадрата (см. рис.).

мкКл, мкКл, м.

Ответ: 43 кВ/м

3.2 З аряды и находятся в соседних вершинах квадрата со стороной . Найти модуль напряженности электрического поля в точке Р, находящейся в центре квадрата (см. рис.). мкКл, мкКл, м.

Ответ: 40 кВ/м

3.3 З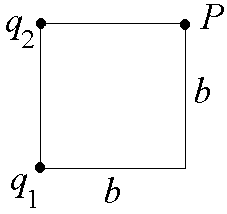 аряды и находятся в соседних вершинах квадрата со стороной . Найти величину горизонтальной проекции напряженности электрического поля в точке Р, находящейся в третьей вершине квадрата (см. рис.). мкКл, мкКл, м.

Ответ: 21 кВ/м

3.4 З аряды и находятся в соседних вершинах квадрата со стороной . Найти величину горизонтальной проекции напряженности электрического поля в точке Р, находящейся на середине противоположной стороны квадрата (см. рис.).

мкКл, мкКл, м.

Ответ: 19 кВ/м

3.5 З аряд находится в вершине квадрата со стороной , а заряд – на середине стороны. Найти модуль напряженности электрического поля в точке Р, находящейся в центре квадрата (см. рис.).

мкКл, мкКл, м.

Ответ: 61 кВ/м

3.6 З аряд находится в вершине квадрата со стороной , а заряд – на середине стороны. Найти величину вертикальной проекции напряженности электрического поля в точке Р, находящейся в центре квадрата (см. рис.). мкКл, мкКл, м.

Ответ: 59 кВ/м

3.7э. Электрическое поле создано точечными зарядами q₁ и q₂. Если q₁ = +q, q₂ = –q, а расстояние между зарядами и от q₂ до точки С равно а, то вектор напряженности поля в точке С ориентирован в направлении ...

а) 1; б) 2; в) 3; г) 4; д) равен 0

3 .8э. Электрическое поле создано точечными зарядами q₁ и q₂. Если q₁ = +q, q₂ = –q, точка С находится на расстоянии а от заряда q₁ и на расстоянии 2а от q₂, то вектор напряженности поля в точке С ориентирован в направлении ...

а) 1; б) 2; в) 3; г) 4; д) равен 0

4. Расчет потенциала электрического поля, созданного дискретными зарядами.

Электростатическое поле точечного заряда характеризуется не только вектором напряженности (см. (3.1)), но и потенциалом :

. (4.1)

Из (4.1) видно, что потенциал – это скалярная величина, которая может быть как положительная, так и отрицательная в зависимости от знака заряда.

Используя принцип суперпозиции полей, можно найти потенциал результирующего электрического поля в заданной точке О как алгебраическую сумму потенциалов полей, созданных каждым зарядом независимо друг от друга (см. рис. 1):

(4.2)