Глава XV . Винтовые линии и винтовые поверхности

В технике часто применяются винтовые по­верхности. Они ограничивают поверхности пружин, червяков, шнеков, сверл, резьб.

Винтовые поверхности образуются с по­мощью винтовых линий, которые играют роль направляющих. Прежде чем приступить к изу­чению образования, изображения и обозначе­ния резьбы, рассмотрим образование винтовых линий и поверхностей.

§ 54. Винтовые линии

Винтовая линия — это пространствен­ная кривая. Она может быть цилиндриче­ской, конической, сферической и т. п.

Цилиндрическая винтовая линия образуется при равномерном перемещении точки вдоль образующей прямого кругового цилиндра, которая, в свою очередь, равно­ мерно вращается вокруг оси цилиндра. Если цилиндру придать равномерно-вращательное движение, а карандашу, приставленному к нему,— равномерно-поступательное (снизу вверх), то на поверхности цилиндра каран­даш оставит след в виде цилиндрической винтовой, линии.

Винтовая линия может быть правой, если линия поднимается, снизу слева вверх напра­во, и левой, если линия поднимается снизу справа вверх налево.

Витком винтовой линии называют линию, описываемую точкой, перемещающей­ся по образующей прямого кругового цилинд­ра за один ее оборот вокруг оси этого ци­линдра.

Ш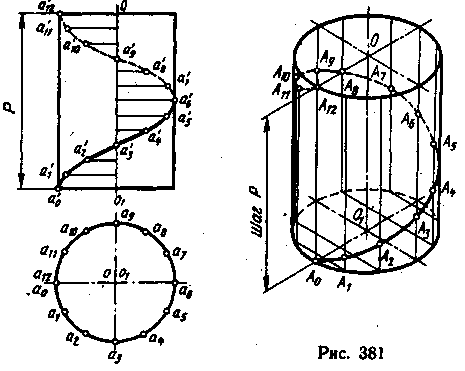 агом винтовой линии называют расстояние между двумя смежными витками. Это расстояние измеряют по образующей цилиндра. На рис. 381 (шаг обозначен буквой Р) показано построение одного витка пра­вой цилиндрической винтовой линии. Для построения винтовой линии делят окружность на 12 равных частей, чтобы на фронтальной проекции зафиксировать 12 положений обра­зующей при ее равномерном вращении вокруг оси цилиндра. Фиксируют положение точки Л, перемещающейся снизу вверх по образую­щей. Зададим шаг винтовой линии и отло­жим это расстояние от нижнего основания вверх по оси цилиндра. Шаг делят на такое же число частей, как и окружность. Разделим шаг на 12 равных частей. Каждое такое деление равно расстоянию, на которое поднялась точка А за время прохождения ¹/₁₂ части витка. За­фиксировав 12 положений точки Л, строят один виток винтовой линии. Для этого точки А₀ — А₁₂ соединяют от руки плавной кривой линией и обводят по лекалу. Фронтальная проекция винтовой линии представляет собой синусоиду, а горизонтальная — окружность.

Коническая винтовая линия обра­зуется при равномерном движении точки вдоль образующей прямого кругового конуса, кото­рая равномерно вращается вокруг оси. Стро­ится она так же, как цилиндрическая винто­вая линия. Окружность основания прямого кругового конуса и заданный шаг делят на равное количество частей и находят поло­жения, точки при движении по вращающейся образующей. Полученные точки соединяют плавной кривой линией и обводят по лекалу.

Фронтальная п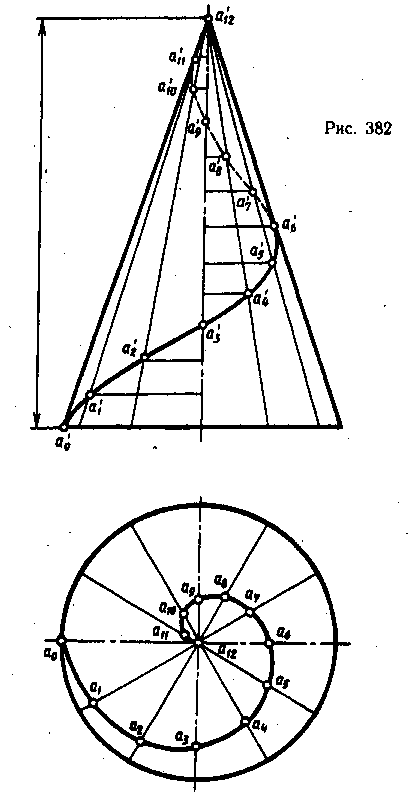 роекция винтовой линии представляет собой синусоиду с затухающей волной, а горизонтальная — спираль Архимеда (рис. 382). Коническая винтовая линия "может быть также правой и левой.

§ 55. Винтовые поверхности

Винтовой поверхностью называют поверхность, которую описывает какая-либо образующая, перемещающаяся по винтовой линии. Такие поверхности могут быть обра­зованы отрезком прямой линии, окружностью или ее дугой, а также любой другой линией.

Рассмотрим винтовые поверхности, образо­ванные отрезками прямой линии. Такие по­верхности называют линейчатыми. Если обра­зующая (отрезок прямой линии) расположена перпендикулярно к оси, то такая поверхность будет называться прямой линейчатой поверхностью. Если образующая накло­нена к оси, то поверхность называется наклонной линейчатой поверхностью.

Н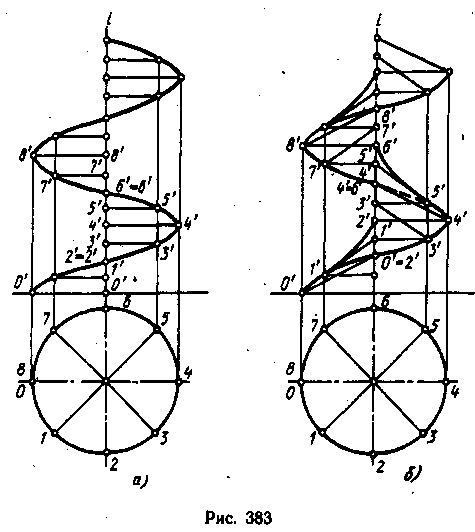 а рис. 383, а показано образование и по­строение прямой линейчатой винтовой поверх­ности, на рис. 383, б — наклонной линейчатой винтовой поверхности. На горизонтальную плоскость проекций винтовая поверхность проецируется в круг.

Строят винтовую поверхность аналогично построению цилиндрической винтовой линии. Шаг и окружность делят на равное количест­во частей. Фиксируют положение образующей через равные промежутки движения. Один конец образующей скользит по оси снизу вверх. Второй конец образующей (отрезка) вращается вокруг оси по винтовой линии, образуя наружный край винтовой поверхности, а сам отрезок (образующая) образует вин­товую поверхность, которая может быть как правой, так и левой, в зависимости от задан­ного направления движения.

Винтовые поверхности часто применяются в технике. Например, прямые и наклонные линейчатые поверхности применяются при кон­струировании ходовых винтов станков, дом­кратов, ручных прессов, в различных резь­бовых изделиях.

Рассмотрим применение винтовых поверх­ностей в резьбовых изделиях. На рис. 384 показано построение витка резьбы прямо­угольного профиля.

Прямоугольник АВСЕ стороной СЕ касается образующей цилиндра диаметром d и, с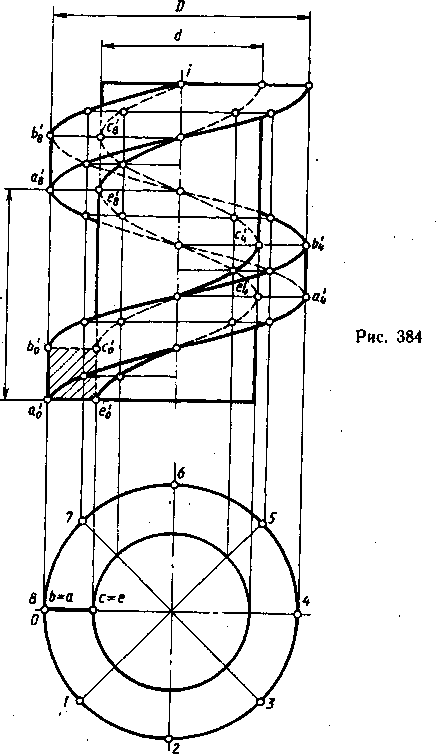 овершая одновременно вра­щательное и поступательное движение относи­тельно оси цилиндра, описывает винтовой выступ, ограниченный двумя винтовыми поверх­ностями, которые образуют отрезки АЕ и ВС, и цилиндрической поверхностью, которую образует отрезок АВ. Построение витка начинают с построения винтовых линий, описываемых точками А и В по наружному диаметру и точ­ками С и £ по внутреннему диаметру. Ког­да производящий профиль (прямоугольник АВСЕ) совершит один полный оборот вокруг оси, он опишет винтовую поверхность — виток и поднимется на расстояние, равное шагу Р. Последующие витки образуются аналогично первому.

Н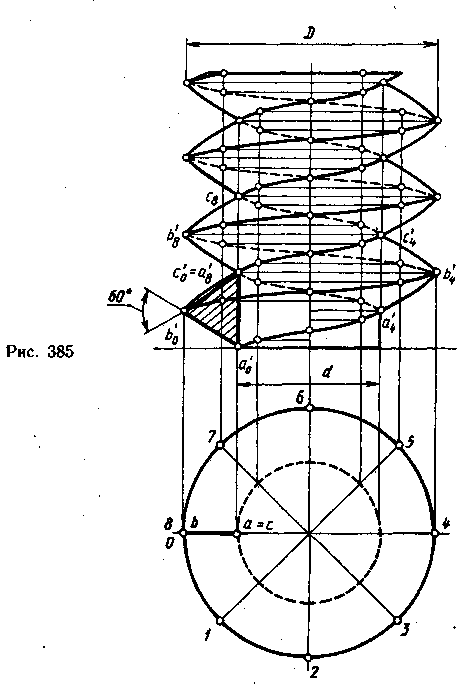 а рис. 385 показано построение витка винтового выступа резьбы, который образуется производящим треугольником ABC. Треуголь­ник ABC стороной АС примыкает к обра­зующей цилиндра диаметра d. Стороны тре­угольника (АВ и ВС) наклонены к оси под углом 60° и при движении образуют наклонные линейчатые винтовые поверхности, которые ограничивают виток резьбы. Для построения витка сначала строят винтовые линии, которые описывают точки Л, В и С при вращательно- поступательном движении треугольника ABC. Точки А а С описывают винтовые линии по. внут­реннему диаметру d, а точка В — по наружному диаметру D.