Лабораторна робота №2

Метрологічна обробка результатів багаторазових

Прямих вимірювань

Мета роботи: вивчення методики метрологічної обробки результатів багаторазових прямих вимірювань та одержання навиків її використання при роботі на персональних комп’ютерах.

1 Короткі теоретичні відомості

Вихідними даними для розрахунку є:

1. масив з п результатів багаторазових вимірювань , , , ... , ;

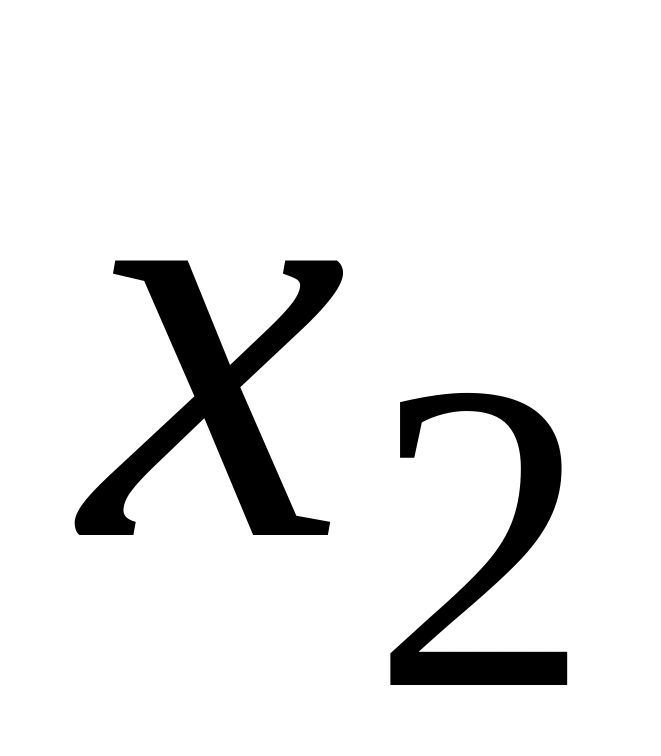2. довірча межа не виключених залишків систематичної складової похибки , яка залежить від інструментальної похибки виміру, похибки методу тощо.

Потрібно обчислити найбільш імовірне значення результату багаторазових прямих вимірювань А та його довірчої межі  А з заданою імовірністю  (в технічних вимірюваннях звичайно = 0,95):

при = 0,95. (2.1)

Такий запис означає – з імовірністю можна стверджувати, що істинне значення вимірюваної величини знаходиться в проміжку між А  А і А + А.

Математична обробка випадкових величин заснована на припущенні, що їх кількість п = , причому закон розподілу цих величин відомий (частіше за все такі величини підпорядковуються нормальному закону розподілу, котрий носить ім’я німецького математика Карла Фрідріха Гаусса). Використання математичної статистики в метрологічних розрахунках засновано на припущенні, що даний кінцевий масив є частиною (вибіркою) з нескінченно великої (генеральної) сукупності результатів спостережень, здійснених в однакових умовах; при цьому параметри, що характеризують дану вибірку, називаються вибірковими або оцінками параметрів генеральної сукупності.

Для нескінченно великої сукупності результатів спостережень, які містять випадкові похибки, істинним значенням вимірюваної величини є середнє арифметичне з усіх результатів спостережень (генеральне середнє). Для кінцевих масивів також можна наближено вважати, що найбільш імовірним значенням результату вимірювання (оцінкою істинного значення шуканої величини) є середнє арифметичне з результатів спостережень, які входять в дану вибірку (вибіркове середнє):

. (2.2)

Оцінка розсіяння результатів спостережень у виборці відносно обчислюється за формулою Бесселя:

. (2.3)

Параметр називається середньоквадратичним вибірковим відхиленням результатів спостережень; і являє собою випадкове відхилення результату i-го спостереження від .

Оцінка середньоквадратичного відхилення найбільш імовірного значення результату вимірювання від його істинного значення обчислюється за формулою:

. (2.4)

З формул (2.3) і (2.4) після елементарних перетворень можна отримати вираз, зручний для обчислень на ЕОМ:

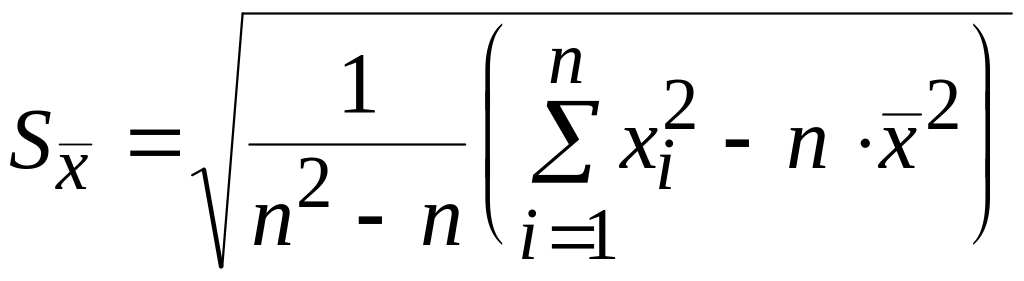. (2.5)

Довірча межа випадкової складової похибки результату

, (2.6)

де - коефіцієнт довіри за Стьюдентом.

Числові значення для різних п при = 0,95 наведені в таблиці 2.1.

Таблиця 2.1 – Значення коефіцієнта довіри для  = 0,95

п		п
2	12,706	7	2,447
3	4,303	8	2,365
4	3,182	9	2,306
5	2,776	10	2,262
6	2,571		1,96

При обчисленні довірчої межі похибки результату А потрібно враховувати як , так і . Для цього треба обчислити параметр , причому:

а) якщо < 0,8, то величиною нехтують і приймають А =  ; (2.7)

б) якщо 0,8   8 , то А = , (2.8)

де

; ; (2.9)

в) якщо > 8, то величиною  нехтують і приймають А = . (2.10)

В числовому виразі для А потрібно обмежуватися, як правило, тільки однією значущою цифрою (тільки якщо перша значуща цифра дорівнює 1, то можна залишати дві значущі цифри). Числове значення А повинно закінчуватися десятковим знаком того ж розряду, яким закінчується А. Результат записується у відповідності з формулою 2.1.

У виробничих умовах, як уже зазначалося, звичайно прямі вимірювання здійснюються одноразово. В цьому разі статистичну обробку результатів вимірювань за наведеними вище формулами не проводять, а щодо точності результатів можна зробити висновок із нормативних метрологічних характеристик вимірювальних приладів (класу точності приладу К_П та його діапазону вимірювання N_П). При цьому надійна межа похибки результату А=θ за формулою (1.10) не вказується, а тільки враховується при заокругленні.