Примеры решения типовых задач

Пример 1. Пусть на расчетный счет в течение n лет в конце года поступает М руб. Проценты начисляются в конце года по ставке i. Определите наращенную сумму и текущую сумму на начальный момент времени данного потока платежей.

Решение. 1. Определим наращенную сумму потока платежей. Первый взнос к концу срока ренты возрастет до суммы , так как на сумму М проценты начислялись в течение (n–1) лет. Второй взнос увеличится до и т.д. На последний взнос проценты не начисляются. Таким образом, в конце срока ренты её наращенная сумма равна

.

Это сумма n-первых членов геометрической прогрессии, в которой первый член равен М, а знаменатель – (1+i). Эта сумма равна

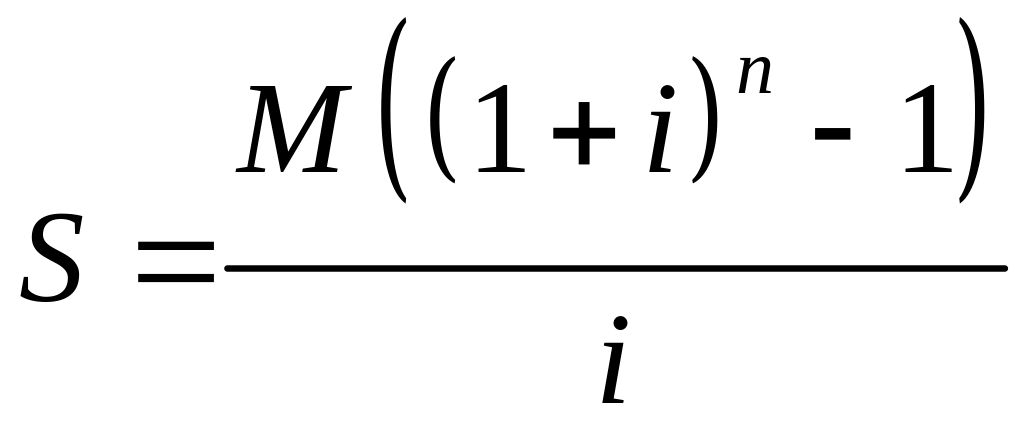руб.

2. Определим текущую сумму потока платежей к началу ренты. Дисконтированная величина первого платежа , второго – и т.д. Таким образом, общая сумма дисконтированных величин равна

.

Это сумма n членов геометрической прогрессии, в которой первый член равен М, а знаменатель – 1/(1+i). Эта сумма равна

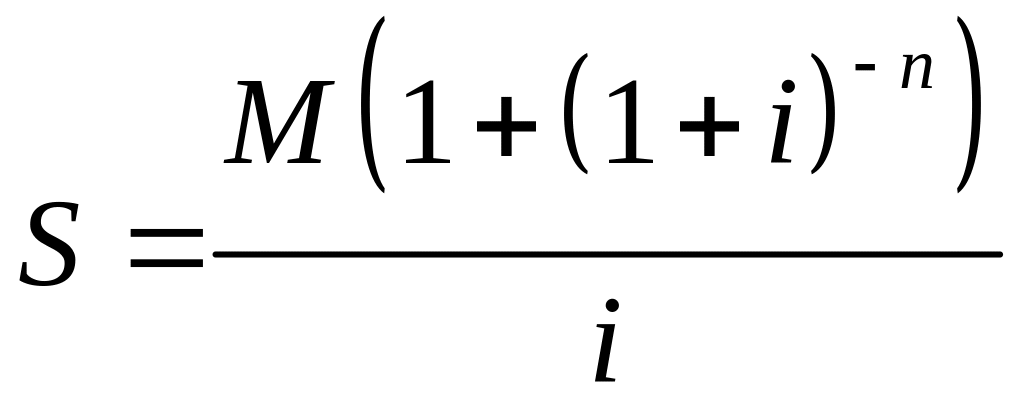руб.

Пример 2. Найдите начальную стоимость вечной ренты, гарантирующей ежегодное поступление на счет М рублей и начисление процентов по ставке i. Обе операции производятся в конце каждого года.

Решение. Повторив рассуждения второй части решения примера 2., представим начальную стоимость вечной ренты в виде бесконечной суммы дисконтированных величин ежегодных платежей:

.

Этот числовой ряд представляет собой бесконечную геометрическую прогрессию, первый член которой равен М/(1+i), а знаменатель q = 1/(1+i). Так как |q| < 1, ряд сходится и его сумма равна

.

Задания для самостоятельной работы

10.17. Господин N планирует накопить за 7 лет 600000 руб. для оплаты обучения сына. Какую сумму он должен в конце каждого месяца вносить на банковский счет при сложной годовой учетной ставке 4 %, начисляемых в конце года?

10.18. Решите задачу 1. при условии, что проценты начисляются ежеквартально.

10.19. Центральный банк РФ покупает правительственные облигации у частных владельцев на 100 миллионов руб. Это создает 100 миллионов «новых» денег и вызывает цепную реакцию банковской системы. Когда эти 100 миллионов поступят на счета частных банков, банки оставят только 15 % в резерве и могут кредитовать остальные 85 %, дополнительно создавая 85 миллионов руб. Компании, которые получают эти деньги, потратят их, а получатели вновь смогут разместить деньги на своих банковских счетах. Предположим, что все эти 85 миллионов повторно депонированы, банки могут снова дать взаймы 85 % этой суммы, создавая 0,85*85 миллионов дополнительных рублей. Этот процесс может быть повторен сколько угодно раз. Вычислите общую сумму «новых» денег, которые могут быть созданы теоретически этим процессом помимо исходных 100 миллионов.

10.20. Пусть Центральный банк РФ, как в задаче 3., выпускает на финансовый рынок 100 миллионов рублей. Частные банки предоставляют в виде кредитов 85 % полученных средств. Предположим, что только 80% каждого кредита повторно депонируется в банках. Таким образом, если общая сумма первого кредитования была равна 0,85*100 миллионов рублей, то вторая общая сумма банковских кредитов составит 85 % от 0,80*0,85*100 миллионов руб. Этот процесс продолжается бесконечно. Определите общую сумму дополнительных средств, которые поступят на финансовый рынок в результате акции Центрального банка РФ.

10.21. Господин N приобрел полис страхования жизни. Согласно договору страховая компания после смерти господина N разместит сумму, равную стоимости полиса страхования, в целевой фонд по ставке 8 %, начисляемых непрерывно. В конце каждого года компания должна выплачивать наследникам 10000 руб. бессрочно. Определите стоимость данного страхового полиса.

10.22. Господин N владеет земельным участком, который сдаёт в аренду за 45000 руб. в год. Арендатор хочет выкупить участок за 1 млн. рублей. Следует ли господину N продать участок, если банковская процентная ставка равна 7 %?

10.23. Определите текущую стоимость бессрочной облигации, генерирующей ежеквартальный поток платежей по 500 руб. при банковской учетной ставке 5 %.

Ответы

10.17. 6217,30 руб. 10.18. 6204,25 руб. 10.19. 566666667 руб. 10.20. 265625000 руб. 10.21. 120066,66 руб. 10.22. Да. 10.23. 40742,38 руб.

Типовые варианты контрольных работ

Контрольная работа № 21 по теме «Числовые ряды»

1. Доказать сходимость ряда и найти его сумму

2. Исследовать на сходимость указанные ряды с положительными членами.

А) ; Б) ; В) ; Г) .

3. Исследовать сходимость знакочередующихся рядов:

а) ; б)

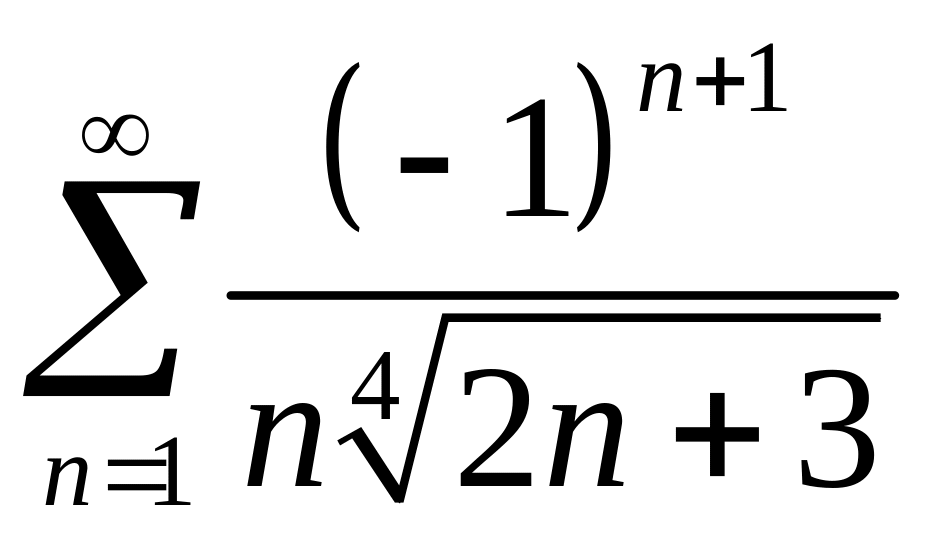
Контрольная работа № 22 по теме «Функциональные ряды»

1. Найти область сходимости рядов:

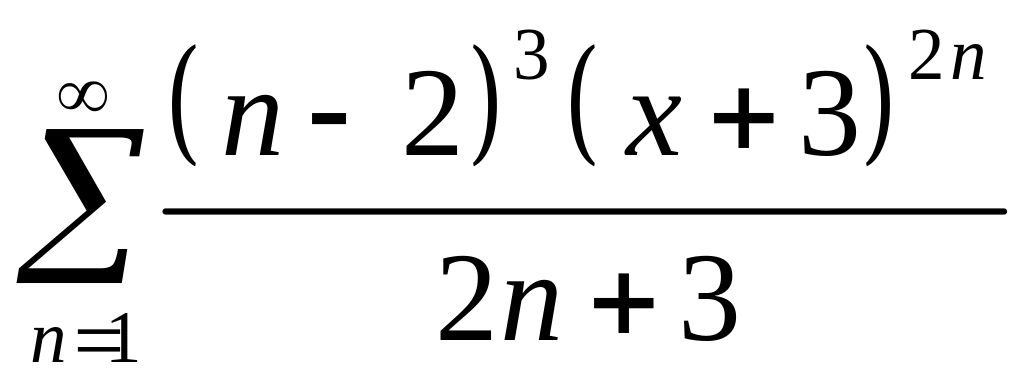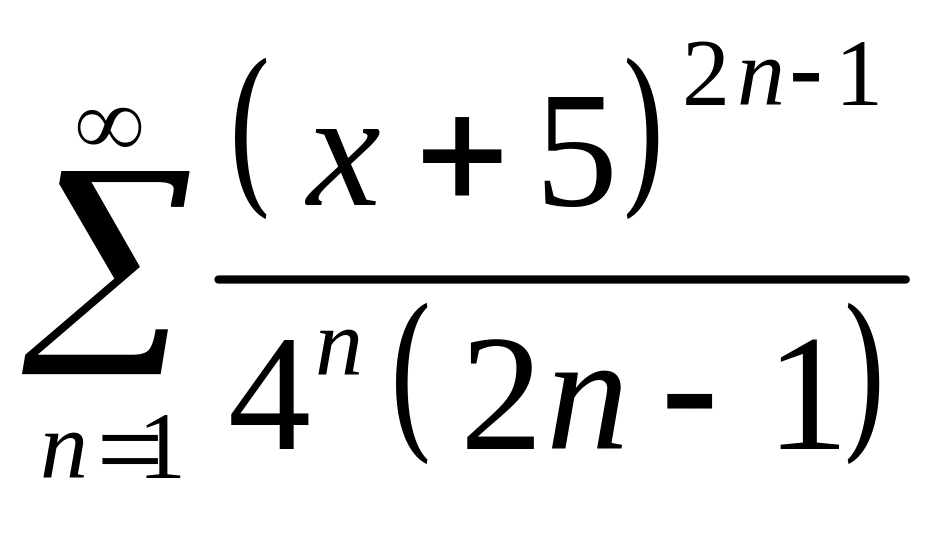а) ; б) ;в)

2. Вычислить интеграл с точностью до 0,001.