10.2. Знакопеременные ряды Краткие теоретические сведения
Определение.
Ряд называют знакопеременным,
если среди его членов есть бесконечно
много как положительных, так и отрицательных
членов. Частным случаем знакопеременного
ряда является знакочередующийся ряд
,
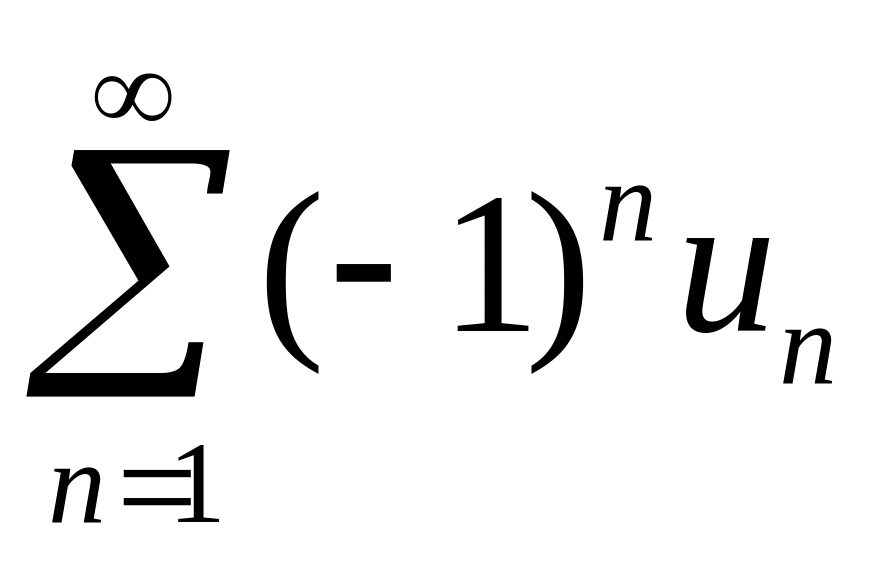где
N:
(1).
Составим ряд (2) из абсолютных величин членов ряда (1):
(2).
Если ряд (1) сходится вместе с рядом (2), то ряд (1)называется абсолютно сходящимся. Если ряд (1) сходится, а ряд (2) расходится, то ряд (1) называется условно сходящимся.
Теорема 1. Сходящийся знакочередующийся ряд (в том числе и знакоположительный) остается сходящимся и не меняет своей суммы при любой группировке его членов, произведенной без изменения порядка их следования.
Теорема 2. Абсолютно сходящийся ряд (в том числе и знакоположительный) остается и не меняет своей суммы при любой перестановке его членов.
Теорема 3. Изменяя порядок следования в условно сходящемся ряде, можно сделать сумму ряда равной любому наперед заданному числу или даже сделать ряд расходящимся.
Теорема 4. Любой абсолютно сходящийся ряд является сходящимся.
Определение.
Признак Лейбница. Если:
1)
–знакочередующийся
ряд;
2)
N:
;
3) ,
то сходится.
Исследование сходимости знакочередующихся рядов следует начинать с исследования их абсолютной сходимости, так как это часто быстрее приводит к цели, чем применение признака Лейбница с последующим исследованием абсолютной сходимости.
Признак
Абеля. Если
для ряда
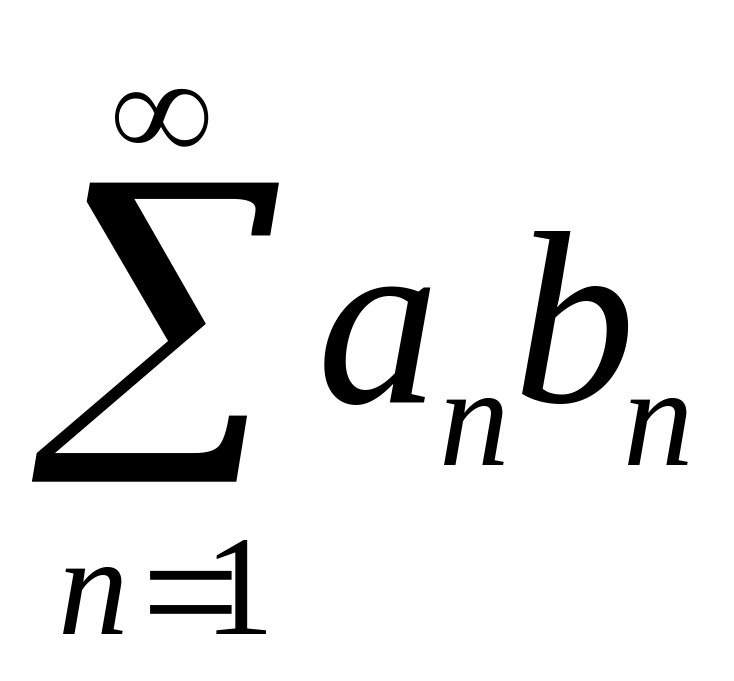выполняются условия:
1)
ряд
сходится;
б)
последовательность
монотонная и ограниченная,
то ряд сходится.
Признак Дирихле. Если для ряда выполняются условия:
а)
последовательность частичных сумм {
}
ограничена;
б)
последовательность {
}
монотонно стремится к 0,
то ряд сходится.
Для
приближенного вычисления суммы
сходящегося ряда
полагают
,
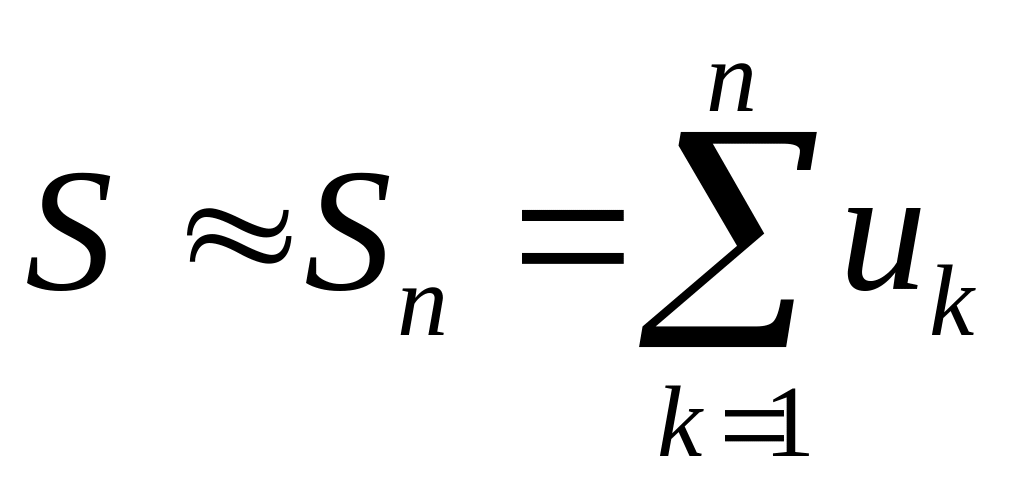пренебрегая остатком
.
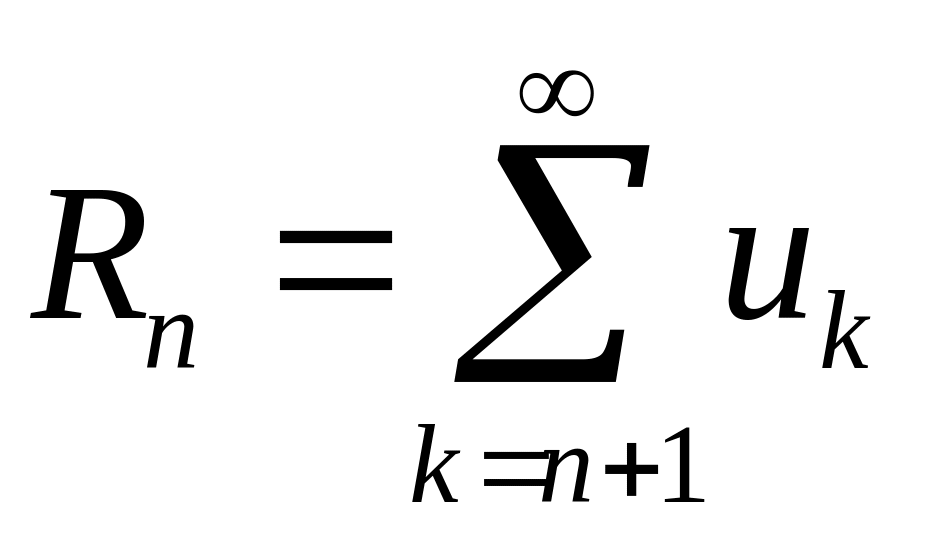Для
сходящихся знакоположительных рядов,
члены которых монотонно убывают, начиная
с
,
справедливы следующие оценки остатка
или
,
где
– общий член ряда.
Примеры решения типовых задач
Пример
1. Исследовать
на сходимость ряд
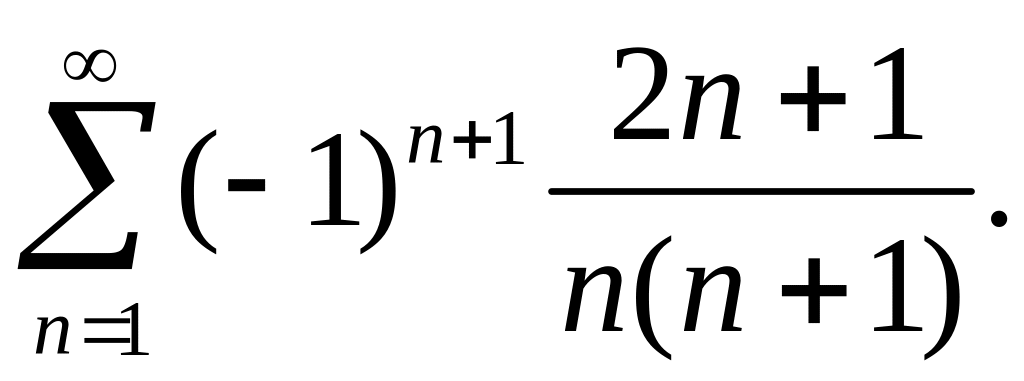
Решение. Этот ряд знакочередующийся. Применим признак Лейбница. Проверим выполнение первого условия.
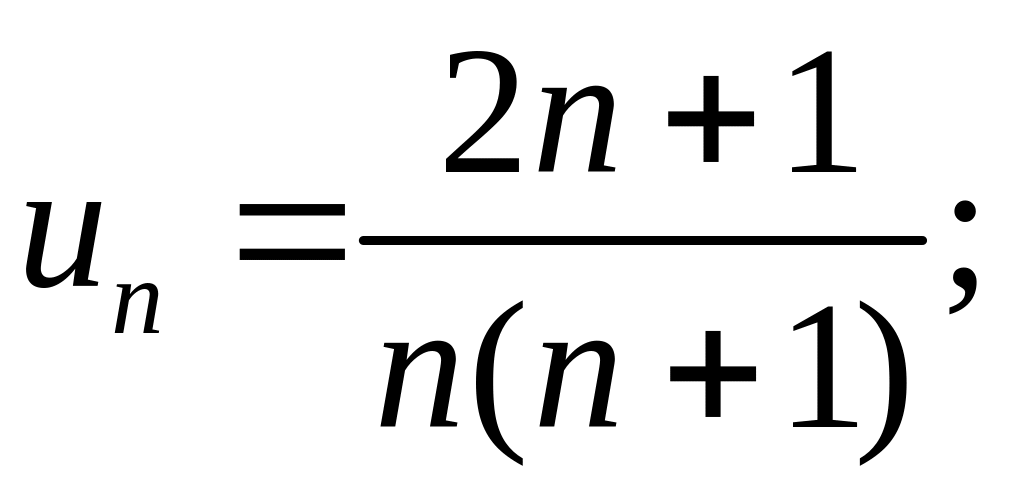
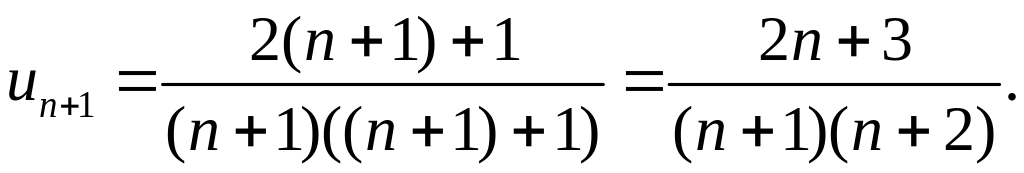
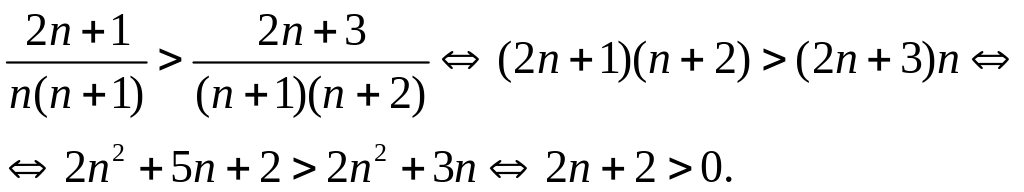
Выполнение
второго условия очевидно
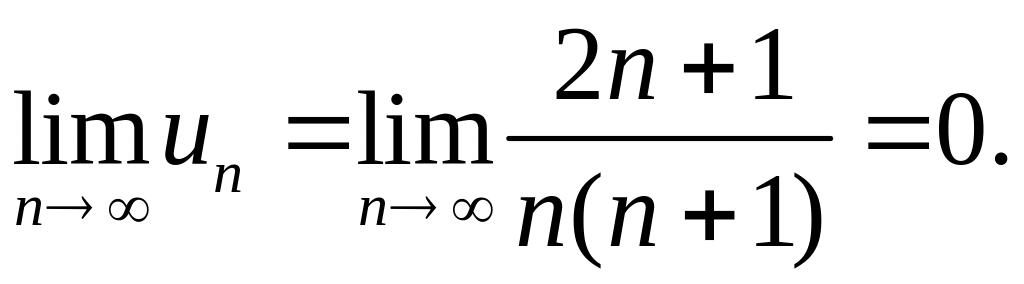Значит, выполнены оба условия признака
Лейбница. Следовательно, данный ряд
сходится. Исследуем на сходимость ряд,
составленный из абсолютных величин
членов первоначального ряда
Покажем, что ряд
и гармонический ряд ведут себя одинаково.
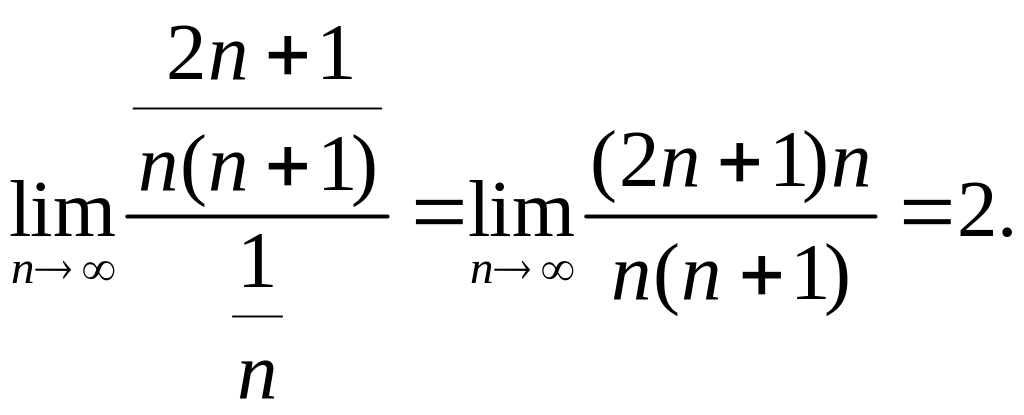Значит
ряд, составленный из абсолютных величин,
расходится. Таким образом, что исходный
ряд сходится условно.
Пример
2. Исследовать
на сходимость ряд.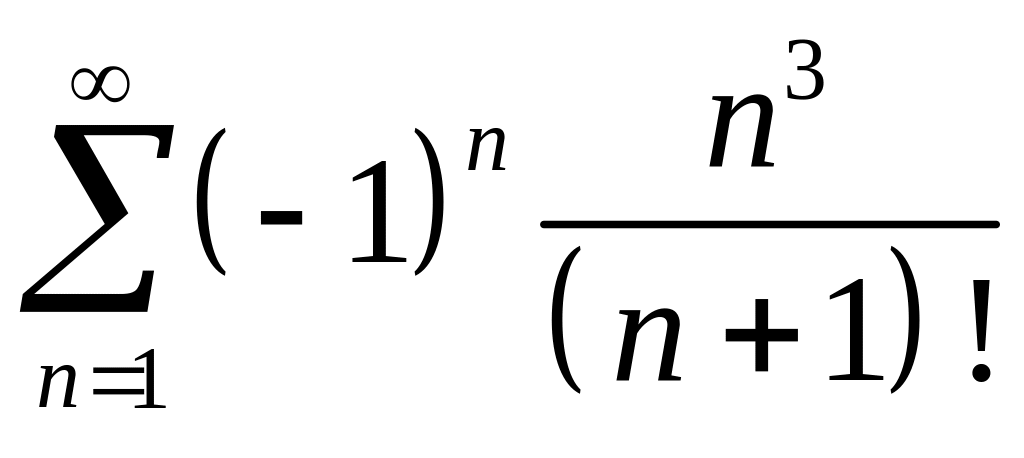
.
Решение.
В данном примере сначала исследуем
знакочередующийся ряд на абсолютную
сходимость, т.е. исследуем сходимость
ряда, составленного из абсолютных
величин членов данного ряда
.
По признаку Даламбера
.
Ряд из абсолютных величин сходится, следовательно, данный знакочередующийся ряд сходится абсолютно.
Пример
3. Найти сумму
ряда
.
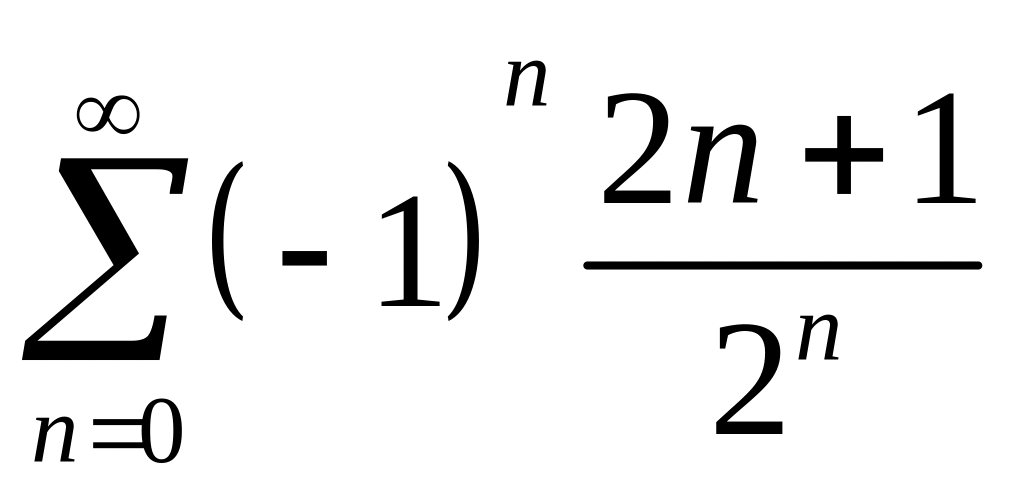Решение.
Составим последовательность частичных
сумм
,
,
,
т.е.
,
тогда
.
Следовательно,
.
Пример
4. Сколько
членов ряда
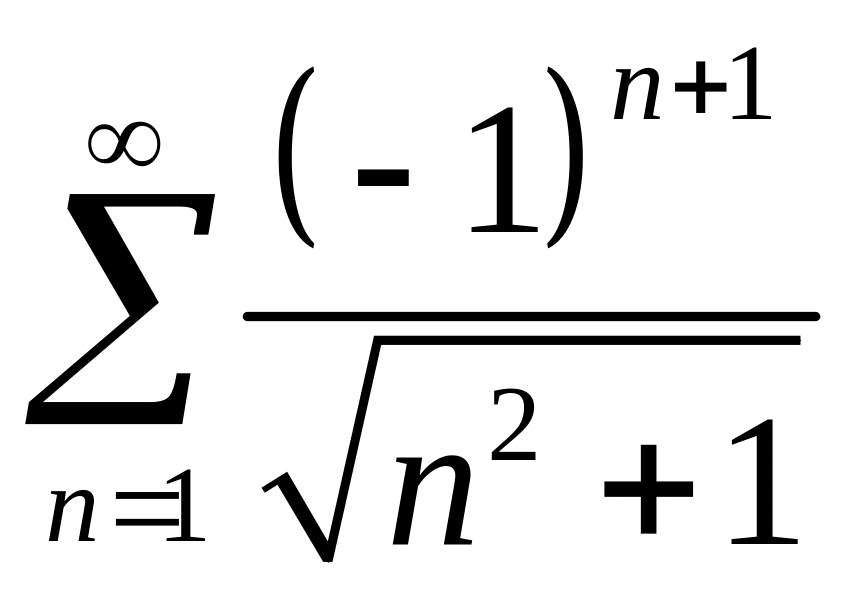следует взять, чтобы получить сумму
ряда с точностью до
?
Решение.
Данный знакочередующийся ряд сходится
по признаку Лейбница. Если возьмем
,
то ошибка не превосходит
.
Но для знакочередующихся рядов остаток
ряда по абсолютной величине не превосходит
величины своего первого члена, т.е.
,
что верно при
.
Отсюда ясно, что достаточно взять 999
членов ряда. Тогда получим требуемую
точность.
Пример
5. Исследовать
на сходимость ряд
.
Решение.
,
поэтому данный ряд имеет вид
.
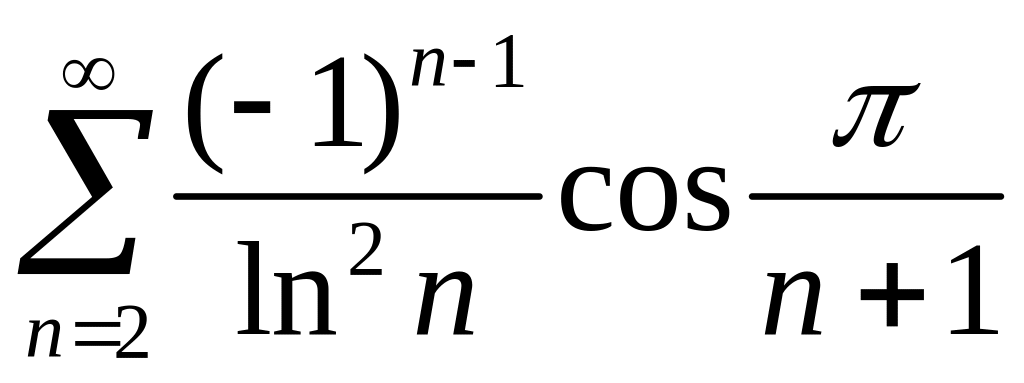Но ряд
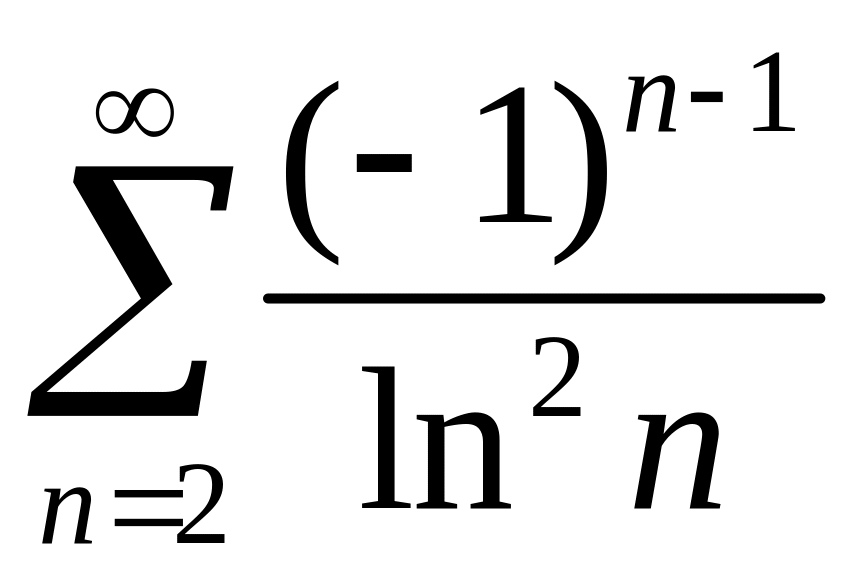сходится по признаку Лейбница, а
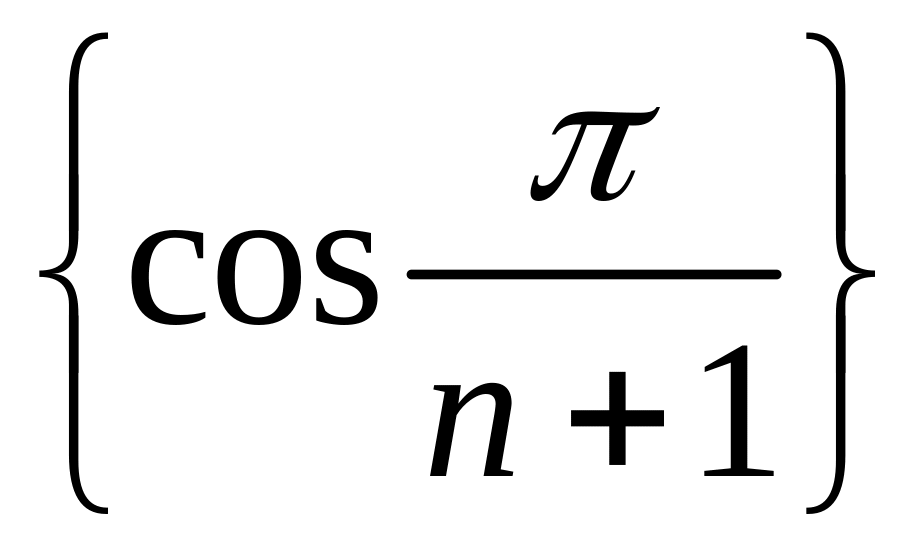монотонная
и ограниченная последовательность.
Значит, по признаку Абеля исходный ряд
сходится.
Рассмотрим
ряд из абсолютных величин
.
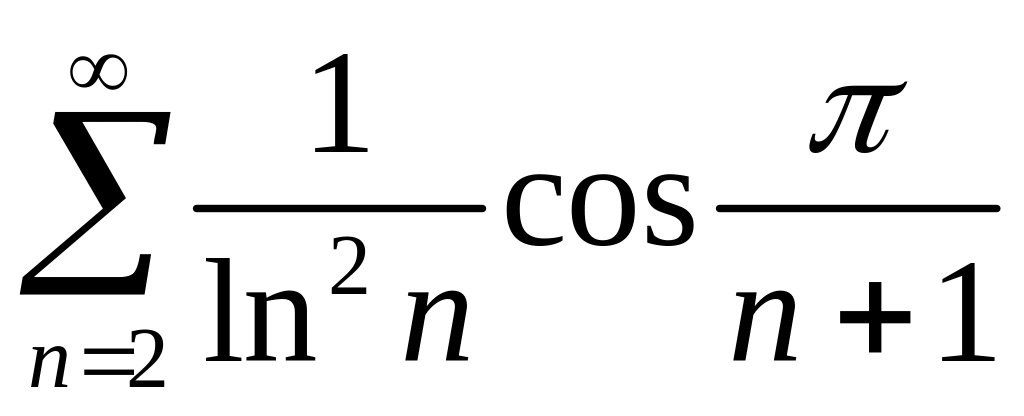Так как
~
при
и
начиная с некоторого
n,
а
расходится, то
расходится. Значит, данный ряд расходится
условно.
Пример
6. Вычислить
сумму ряда
с точностью до
0,001.
Решение. Для знакочередующихся рядов погрешность не превышает первого отброшенного члена.
.
,
,
,
.
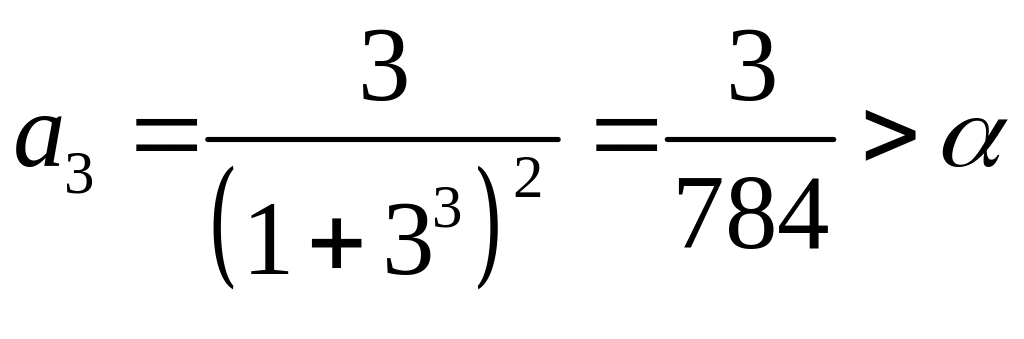Поэтому
искомая сумма с точностью до
равна
.
Задания для самостоятельной работы
10.8. Исследовать ряд на абсолютную и условную сходимость:
а) |
б) |
в) |
г) |
д) |
е) |
ж) |
з) |
;
;
;
;
;
;
;
.10.9. Вычислить сумму ряда с точностью :
а) |
б) |
в) |
г) |
д) |
е) |
ж) |
з) |
;
;
;
;
;
;
;
.Ответы
10.8. а) абсолютно сходится; б) сходится условно; в) сходится абсолютно; г) сходится абсолютно; д) сходится условно; е) сходится условно; ж) сходится абсолютно; з) сходится условно. 10.9. а) 0, 18127; б) 0,633; в) 0,112; г) –0,303; з) 0,5.
10.3. Функциональные ряды
Краткие теоретические сведения
Определение
1. Ряд, членами
которого являются функции аргумента
,
определенные на некотором множестве
,
называется функциональным:
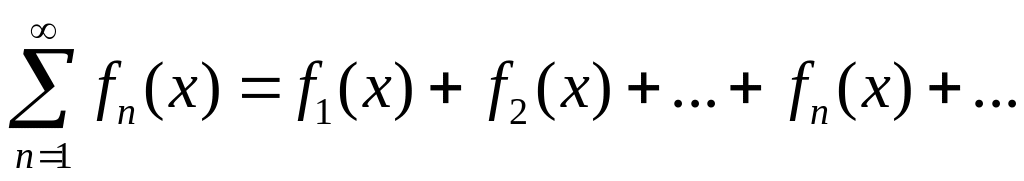
Множество всех значений , при которых функциональный ряд становится сходящимся числовым рядом, называется областью сходимости функционального ряда.
Может
случиться, что для некоторых
ряд сходится абсолютно, а для некоторых
условно.
Для нахождения областей сходимости функциональных рядов можно использовать разложение основных элементарных функций в ряд и достаточные признаки сходимости числовых рядов.
Определение
2.
Суммой функционального ряда называется
функция
,
где
-я
частичная сумма.
Определение
3. Сходящийся
в некотором промежутке
функциональный ряд
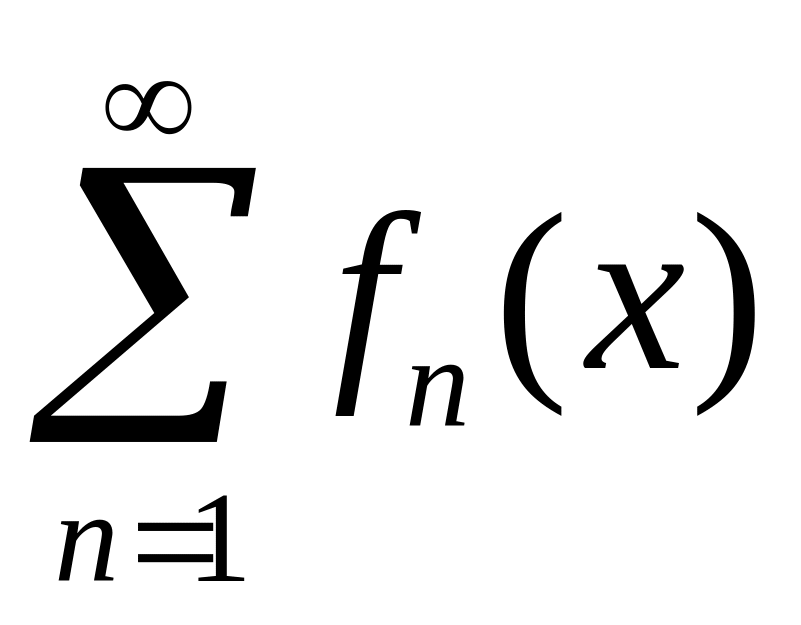называется равномерно
сходящимся
в этом промежутке, если для любого
существует номер
,
не зависящий от
и такой, что для всех
справедливо неравенство
одновременно для всех значений
рассматриваемого промежутка.
Теорема
1. Если членами
функционального ряда
являются непрерывные
в некотором промежутке функции
и в этом промежутке ряд сходится
равномерно, то его сумма
непрерывна в этом промежутке.
Теорема
2 (признак Вейерштрасса).
Если члены функционального ряда
в некотором промежутке Е
не
превосходят по абсолютной величине
соответствующих членов сходящегося
числового ряда
с положительными
членами, т.е. если для всех
Е:
,
то данный функциональный ряд сходится
в этом промежутке абсолютно и равномерно.
Числовой ряд называется мажорирующим рядом или числовой мажорантой для функционального ряда на промежутке.
Теорема
3. Если членами
функционального ряда
являются непрерывные на промежутке
функции, и ряд сходится равномерно на
этом отрезке к функции
,
то его можно почленно проинтегрировать
на этом отрезке:
.
Выше сформулированы достаточные условия для почленного интегрирования рядов. Существуют ряды, не удовлетворяющие условиям этой теоремы, но допускающие почленное интегрирование.
Теорема 4. Если в некотором промежутке:
функциональный ряд сходится к сумме ;
члены
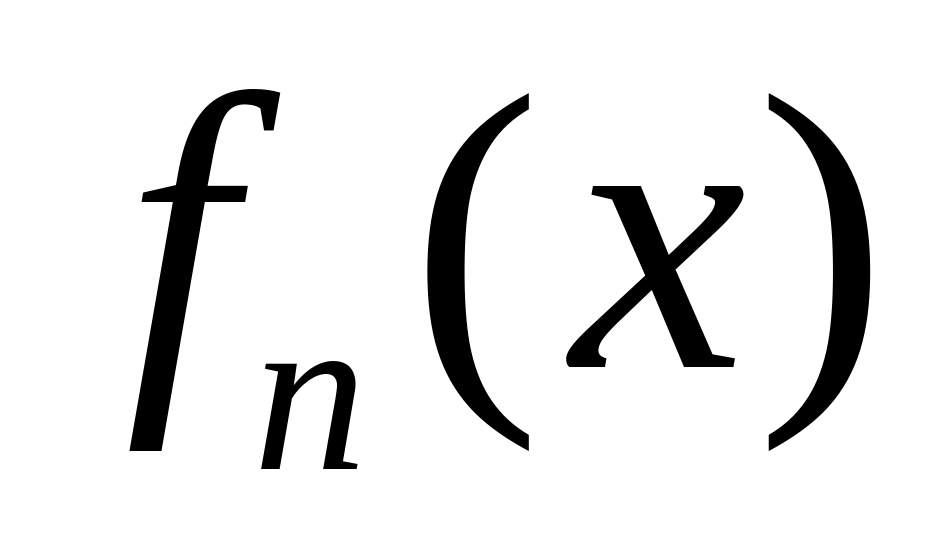данного ряда имеют непрерывные
производные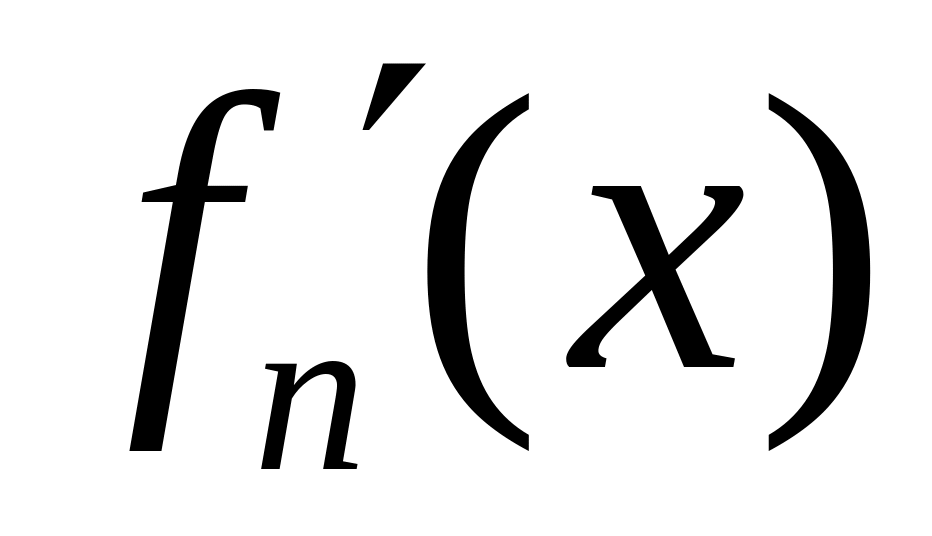
;ряд этих производных
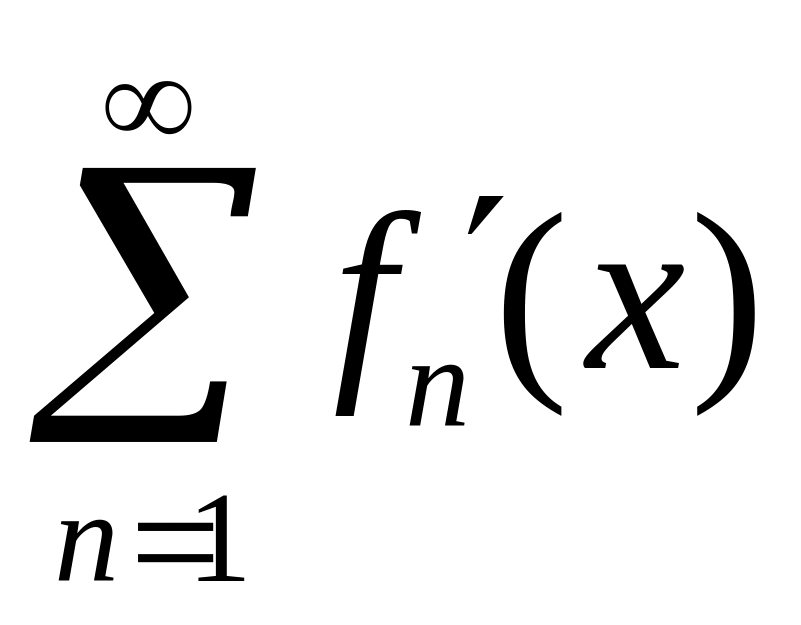сходится
равномерно; то данный функциональный
ряд можно почленно дифференцировать
в каждой точке упомянутого промежутка:
.
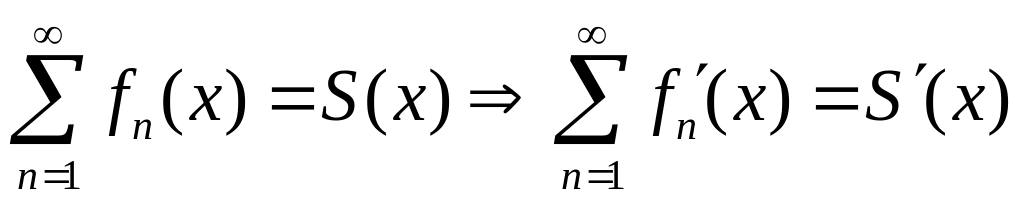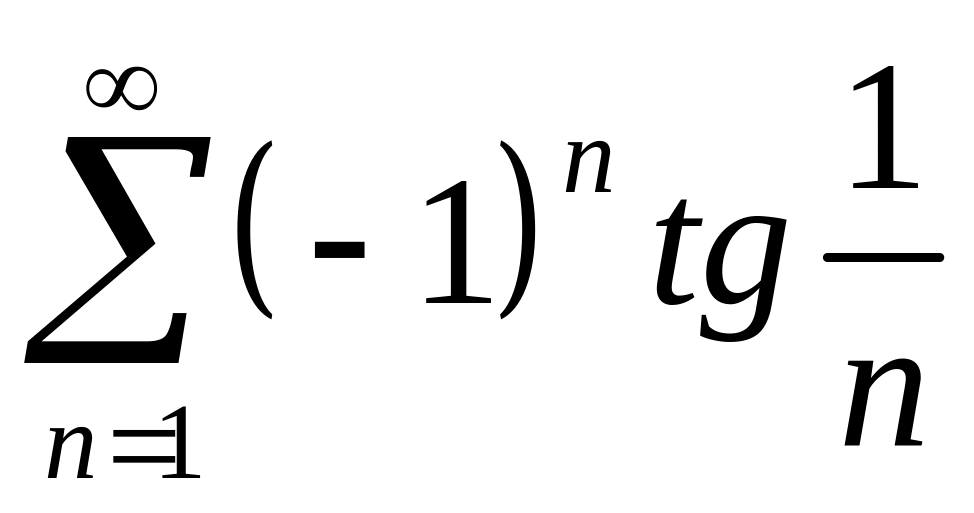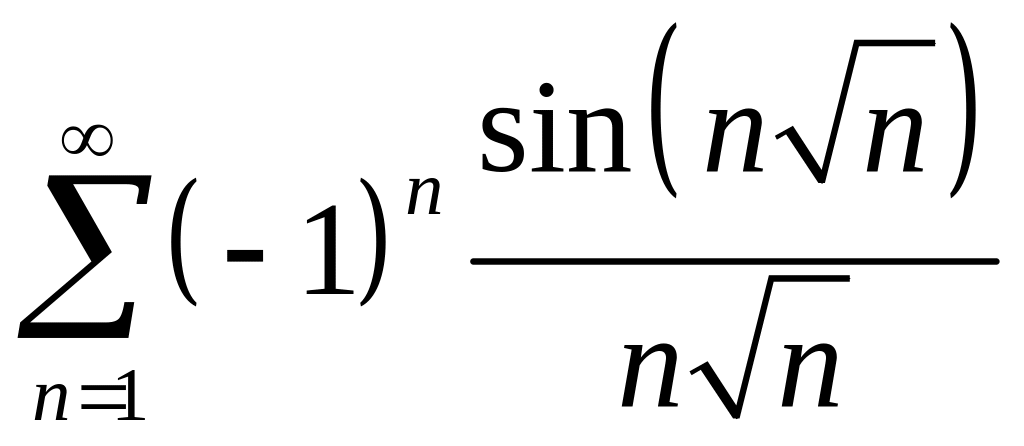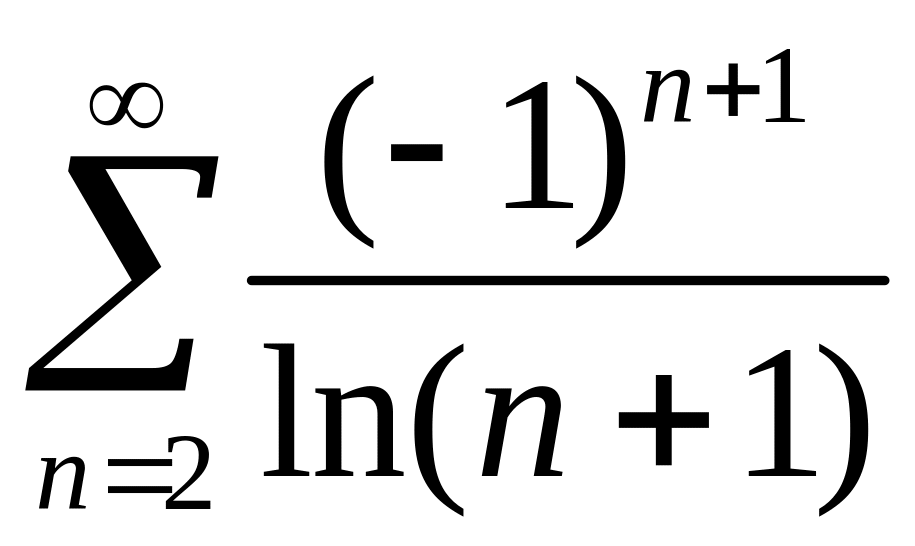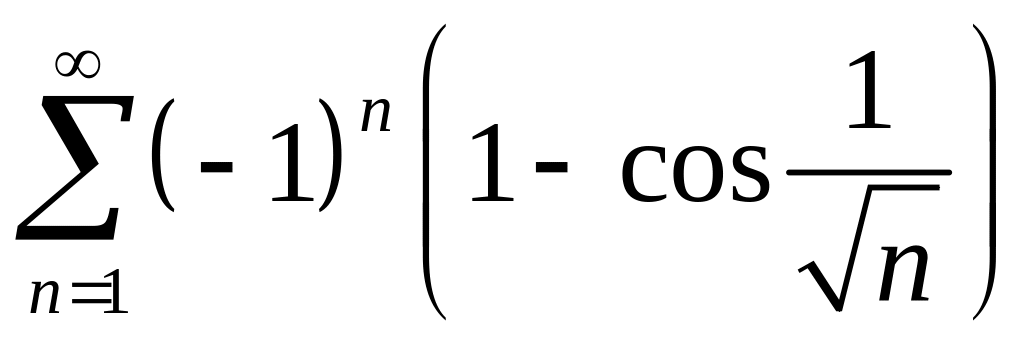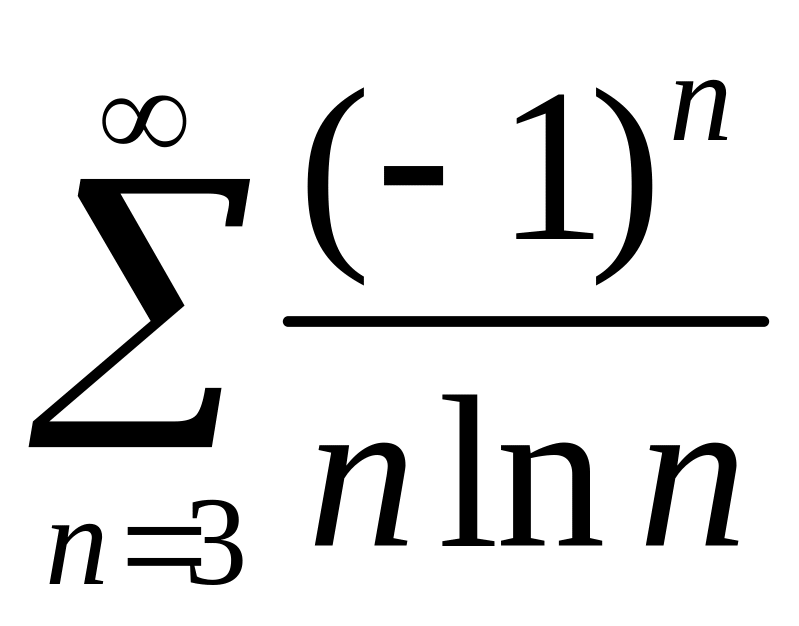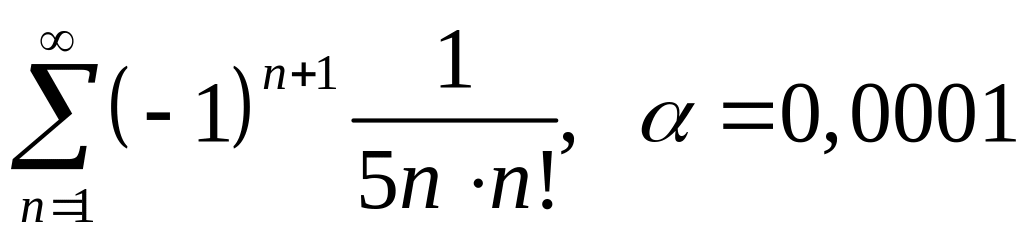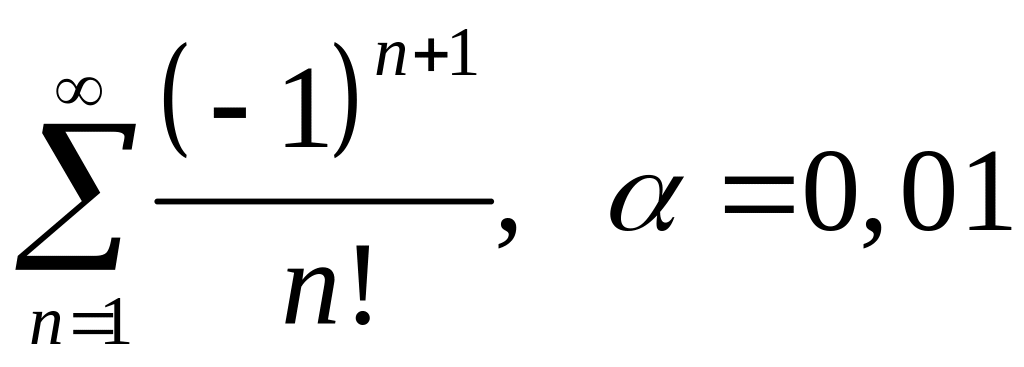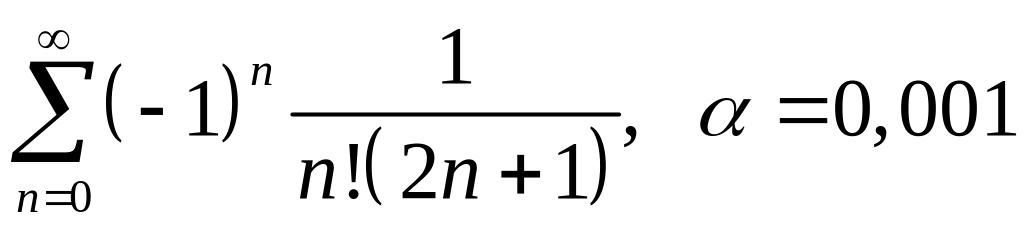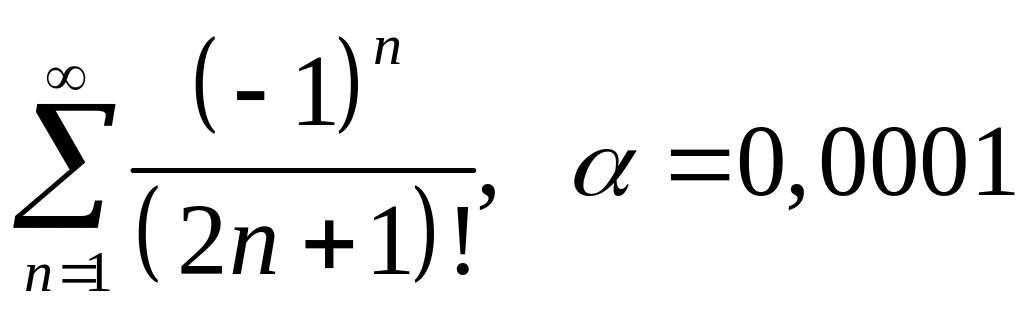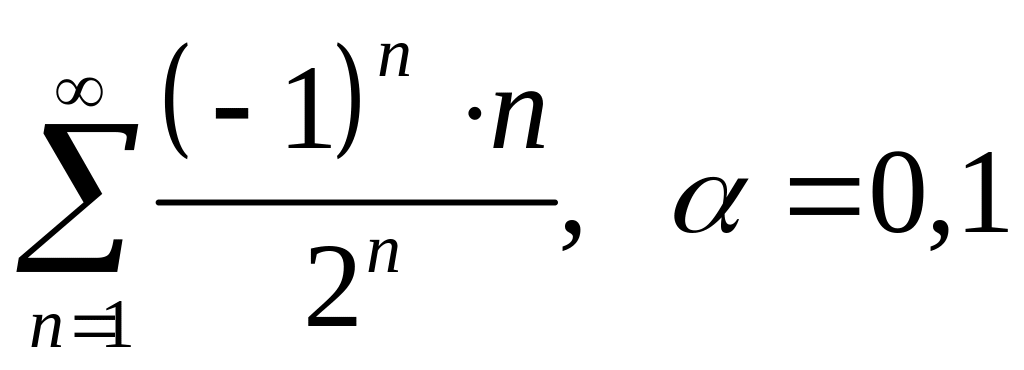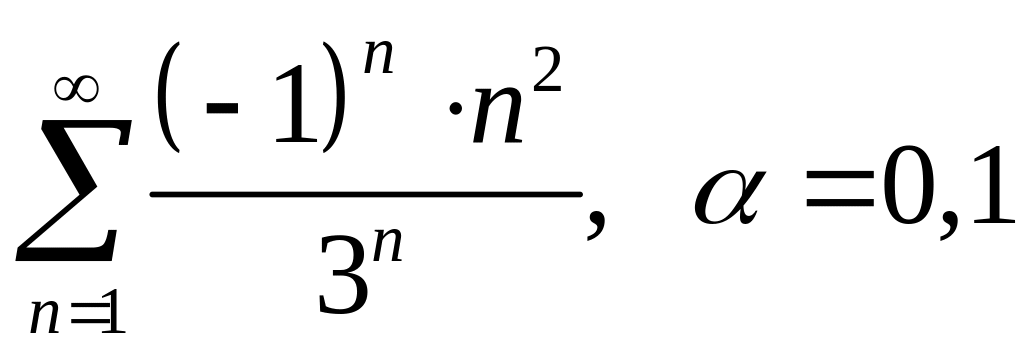