2.3. Множення на елементарнi матрицi

Припустимо спочатку, що розглядаємо матрицi якогось фiксованого розмiру, наприклад,

Означення. Матриця, у якої якийсь один елемент дорiвнює одиницi, а решта елементiв дорiвнюють нулю, називається матричною одиничкою. Коли в деякої матричної одинички вiдмiнний вiд нуля елемент знаходиться на мiсцi з номером , тодi ця матрична одиничка позначається .

Зауваження. У позначеннi матрицi не вказується, якого розмiру має бути матрична одиничка – завжди мається на увазi, що розмiри матрицi вiдомi.

Наведемо приклади матричних одиничок. Якщо розглядаємо матрицi розмiру то матричною одиничкою є матриця . Якщо ж ми розглядаємо матрицi розмiру то матричною одиничкою є матриця .

Означення. Квадратна матриця розмiру називається елементарною, якщо вона має один з таких виглядiв:

1. є дiагональна матриця у якої дiагональний елемент дорiвнює а решта дiагональних елементiв дорiвнюють : Такi елементарнi матрицi називаються iнколи елементарними дiагональними.

2. є матриця , тобто в матрицi

• усi дiагональнi елементи дорiвнюють ;

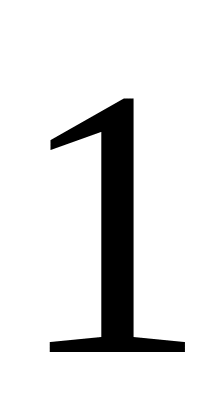• елемент з номером дорiвнює ;

• решта елементiв матрицi дорiвнюють нулю.

Такi елементарнi матрицi називаються iнколи елементарними трансвекцiями.

Одинична матриця є звичайно елементарною. Довільна ненульова матриця розміру є елементарною.

Приклади елементарних матриць:

, ,

.

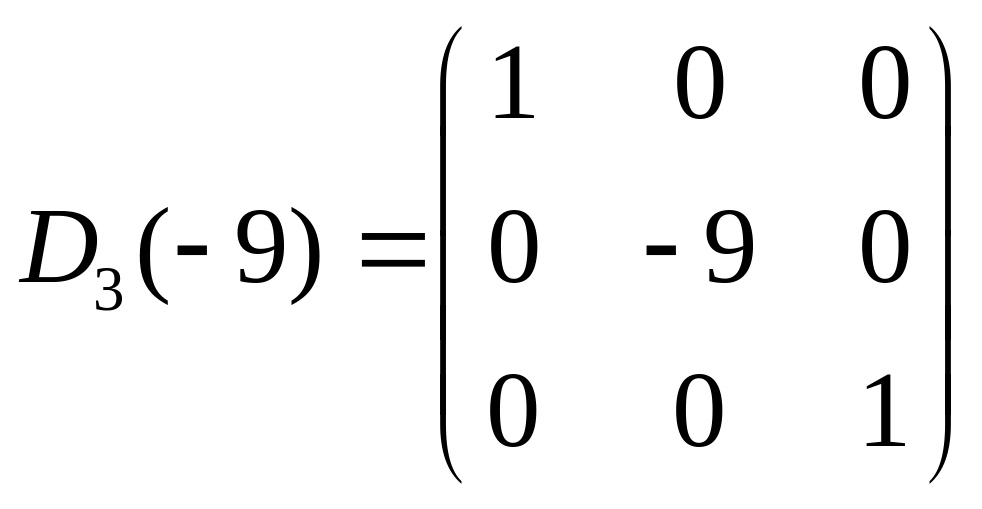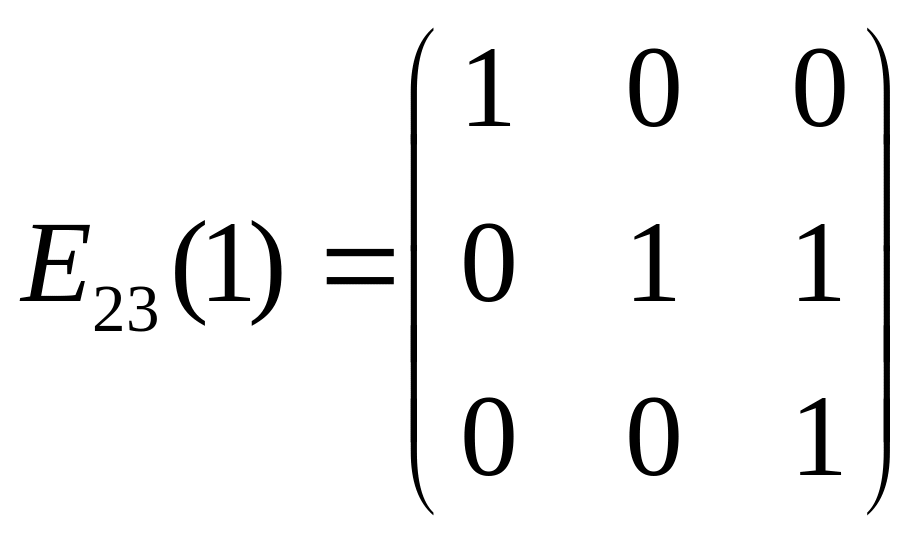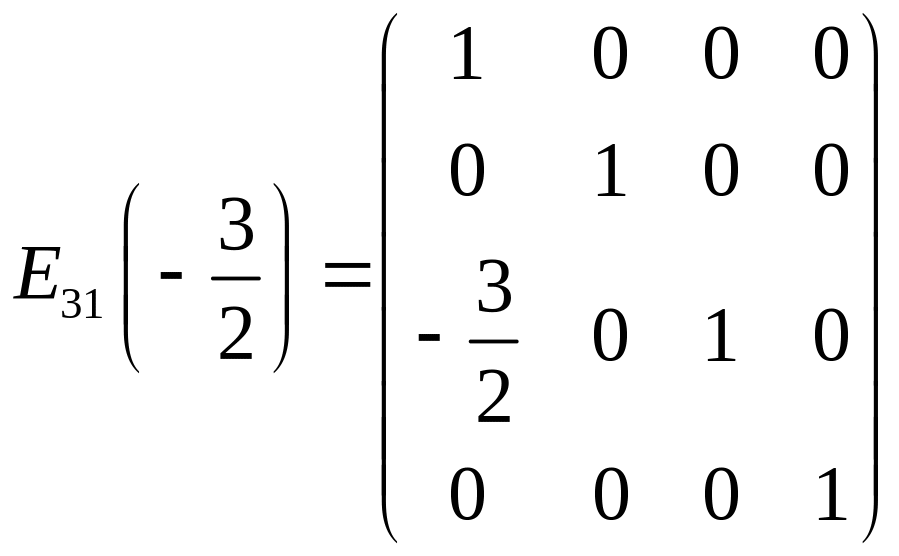Звичайно, елементарні матриці тісно пов'язані з елементарними перетвореннями.

Нехай  – довiльна -матриця. Елементарні перетворення рядків матрицi еквівалентні множенням зліва матриці на відповідні елементарні -матриці, а саме:

1) помножити -тий рядок матрицi на деяке число – це те саме, що виконати множення матриць ;

2) додати до -того рядка матрицi -тий, , помножений на деяке число – це те саме, що виконати множення .

Елементарні перетворення стовпчиків матрицi еквівалентні множен-ням справа матриці на відповідні елементарні -матриці, а саме:

1) помножити -тий стовпчик матрицi на деяке число – це те саме, що виконати множення матриць ;

2) додати до -того стовпчика матрицi -тий, , помножений на деяке число – це те саме, що виконати множення .

Приклад. Розглянемо питання, на яку матрицю треба помножити матри-цю , щоб виконати перестановку -того та -того стовпчиків. Оскільки перестановка стовпчиків матриці є композицією елементарних перетворень стовпчиків типу 1) та 2), то відповідна матриця буде добутком елементарних. Маємо ланцюжок перетворень і відповідних множень матриць:

.

Наприклад, у випадку , щоб переставити перший та третій стовпчики, слід помножити матрицю справа на матрицю

.

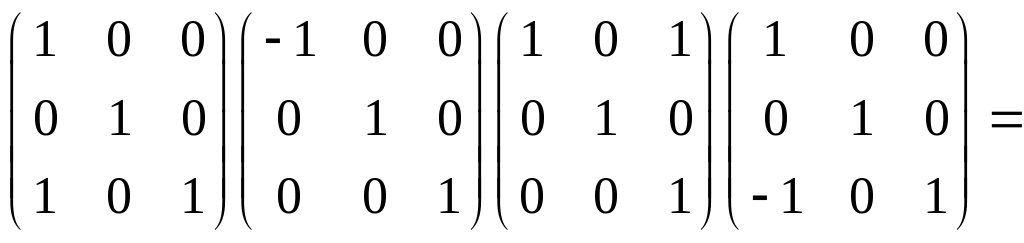
У загальному випадку, щоб переставити -тий та -тий рядки (або стовпчики) матриці розміру , треба помножити матрицю зліва на матрицю (або, у випадку перестановки стовпчиків, справа на ту саму матрицю ).

2.4. Обернені матриці

Означення. Нехай – деяка квадратна -матриця. Тоді матриця розміру називається оберненою до матриці , якщо 1) та 2) .

Зауваження. 1. У наведеному вище визначенні достатньо вимагати виконання однієї з двох умов 1) або 2): якщо , то звідси випливає, що . Навпаки, якщо , то обов'язково виконується .

2. Не для будь-якої матриці існує обернена. Наприклад, для нульової матриці не існує оберненої.

3. Якщо для матриці існує обернена, то лише одна.

Матрицю, обернену до , позначають .

Матриця , для якої існує обернена , називається оборотною.

Твердження. Якщо для -матриць та існують обернені, то матриця також має обернену, причому .

Згідно з попереднім зауваженням, для доведення достатньо лише перевірити, що .

Укажемо обернені до елементарних матриць:

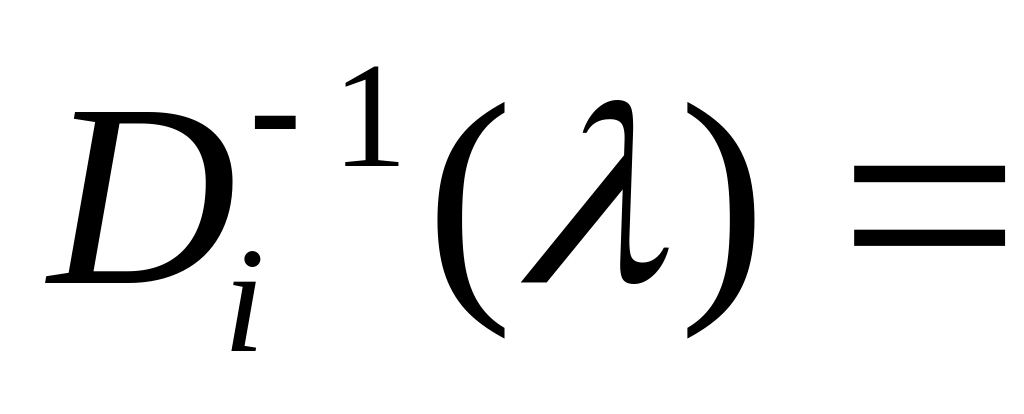
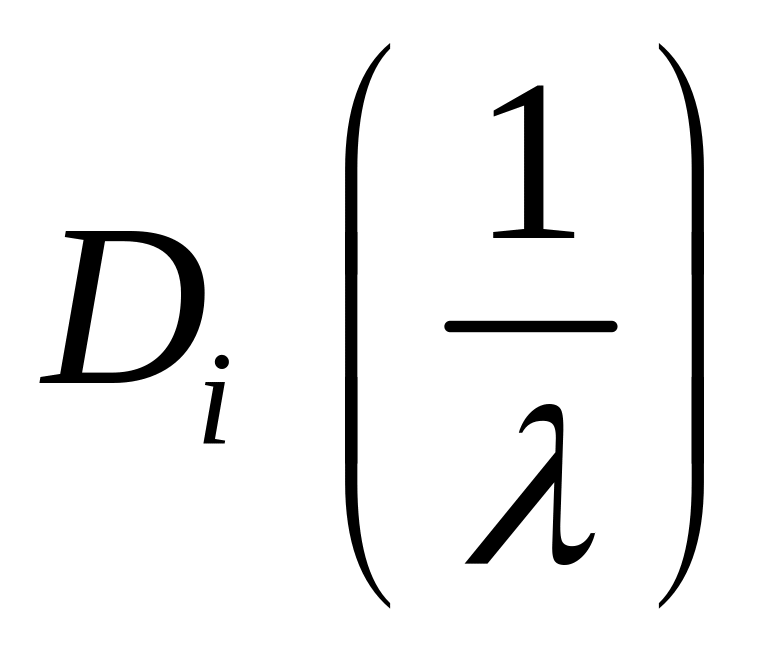• , де ;

• .

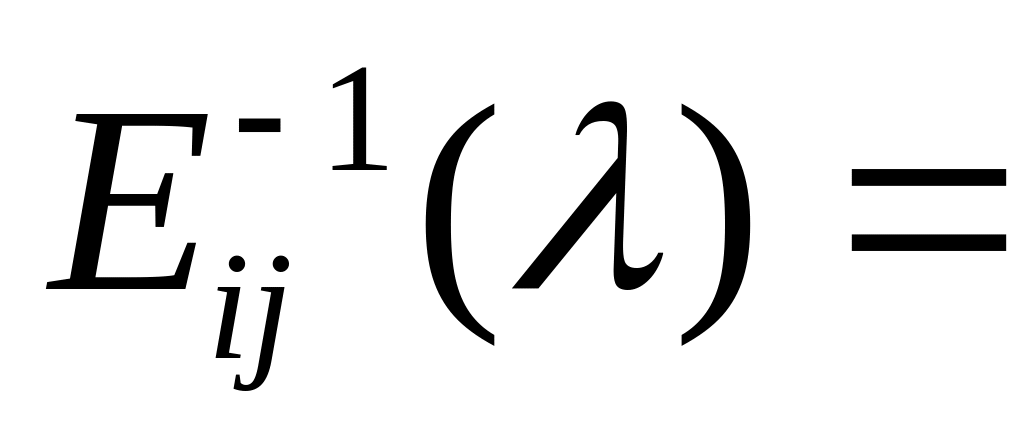
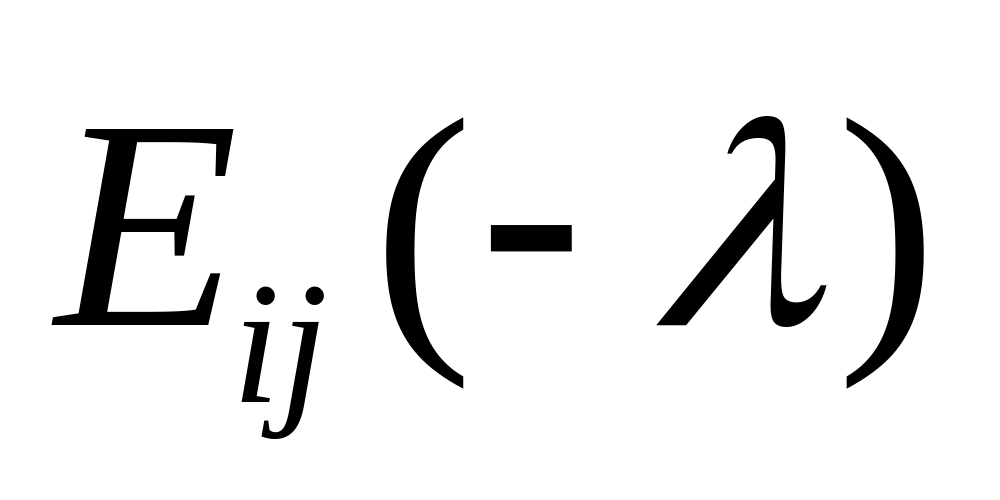Перевірте!