4.4. Формула для обчислення визначника

Iснує формула, що дозволяє порахувати значення визначника як багаточлена вiд коефiцiєнтiв матрицi.

Формула для обчислення має, головним чином, теоретичне значення.

Факт. Нехай , , є деяка -матриця. Тодi визначник матрицi обчислюється за формулою

,

де через позначається кількість інверсій пiдстановки . Іншими словами, одночлен входить у формулу для обчислення детермінанта зі знаком плюс, якщо підстановка парна, і зі знаком мінус у протилежному випадку.

Зауваження. 1. Указана сума мiстить доданкiв, по одному для кожної пiдстановки . Наприклад, формула для обчислення визначника 5-го порядку мiстить членiв, формула для визначника 6-го порядку мiстить . Велика кiлькiсть доданкiв значно ускладнює практичне використання вказаних формул.

2. Для у наведенiй формулi кожен одночлен мiстить

– один і лише один спiвмножник з кожного стовпчика матрицi ;

– один і лише один спiвмножник з кожного рядка матрицi .

Задачa. Записати формулу для визначника матрицi третього порядку , , як багаточлена вiд .

Розв'язання. Шуканий багаточлен мiстить доданкiв вигляду , де пробiгає множину пiдстановок на трьох елементах. Щоб побудувати цей багаточлен, випишемо всi пiдстановки з , їх парнiсть та вiдповiднi одночлени.

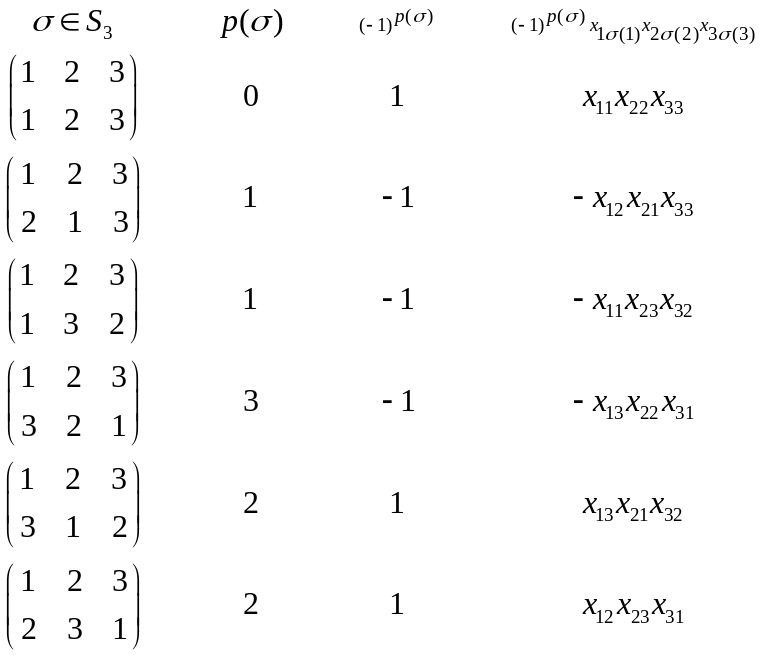
Отже, можемо записати вiдповiдь

Вiдповiдь.

.

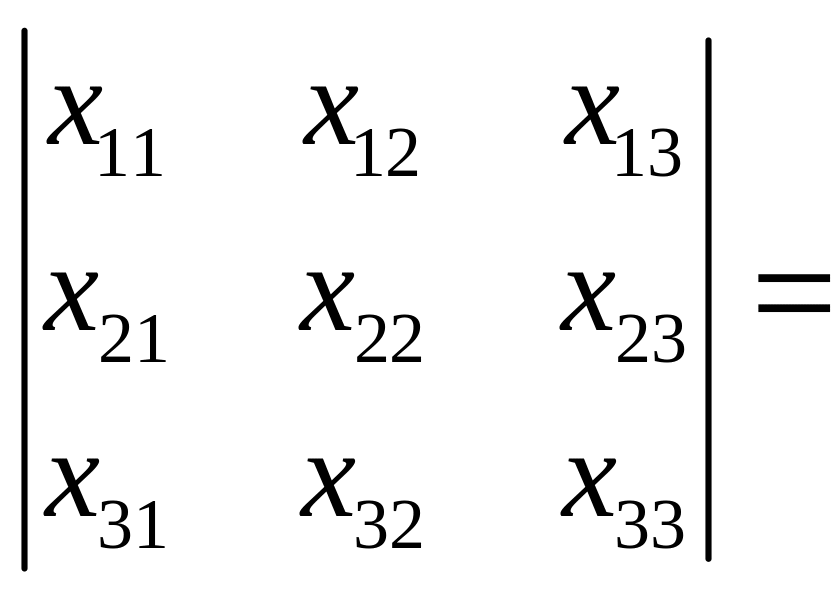
Задачa. Записати доданок з формули для визначника матрицi , , котрий вiдповiдає пiдстановцi

.

Розв'язання. Щоб визначити, чи є вказана пiдстановка парною або ж непарною, порахуємо кiлькiсть iнверсiй у другому рядку вiдповiдної таблицi. Це iнверсiї , , , . Отже, і вiдповiдний доданок дорівнює

.

Вiдповiдь. .

Задачa. Вiдомо, що визначник матриці

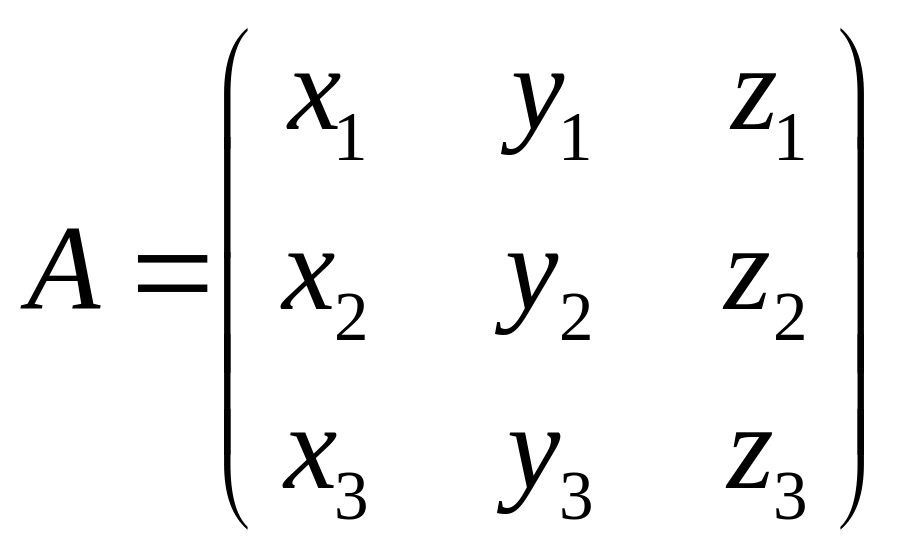
дорiвнює . Чому дорiвнює визначник матриці

?

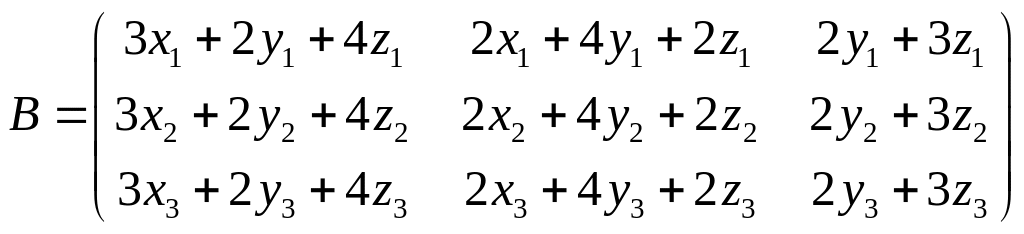Розв'язання.

Спосiб 1. Позначимо вектори - стовпчики матрицi через та :

, , .

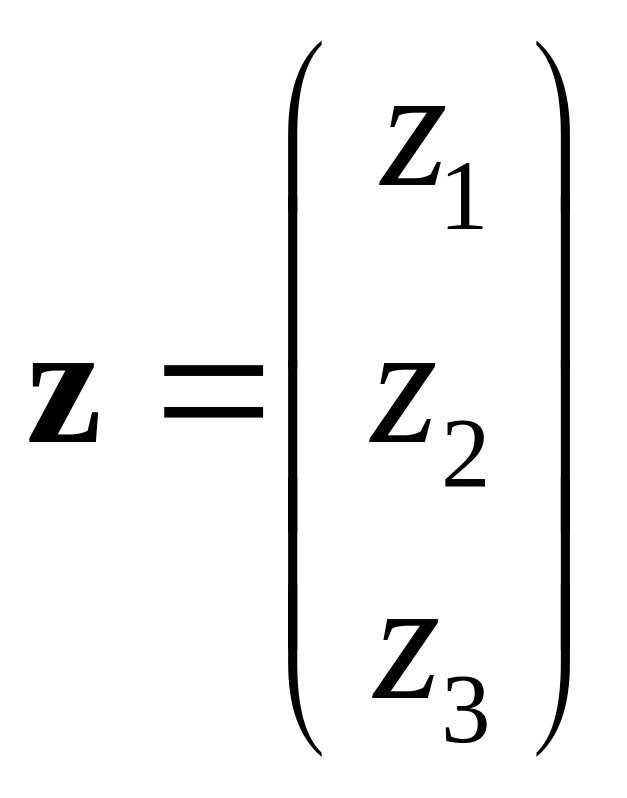Тодi матрицю можемо записати у вигляді

,

а матриця , має вигляд

.

Намагаємось виконувати такі елементарні перетворення стовпчиків, в результаті яких матриця зведеться до матриці , визначник якої нам відомий.

Можемо винести множник з другого стовпчика, при цьому детермiнант матрицi, що залишиться, роздiлиться на коефiцiєнт .

Винесемо з другого стовпчика. При цьому визначник змiниться у разів.

.

Винесемо з третього стовпчика коефiцiєнт, що дорівнює , при цьому визначник змiниться на разів. Одержимо матрицю . При перестановцi другого та третього стовпчикiв визначник множиться на i матриця, яку одержимо в результатi, буде: .

Таким чином, щоб одержати визначник матрицi , необхiдно визначник матрицi, яку ми одержали (тобто ) помножити на коефiцiєнт .

Отже, .

Скорочено цю послідовність перетворень матриці можна записати як такий ланцюжок перетворень визначників:

.

Спосiб 2. Як i в попередньому випадку, позначимо вектори-стовпчики матрицi через і :

, , ,

, .

Запишемо коефiцiєнти при у перший рядок, при  – у другий, при  – у третiй стовпчик деякої матрицi та позначимо її через :

.

Має мiсце рiвнiсть . Але тоді . Можна пiдрахувати

.

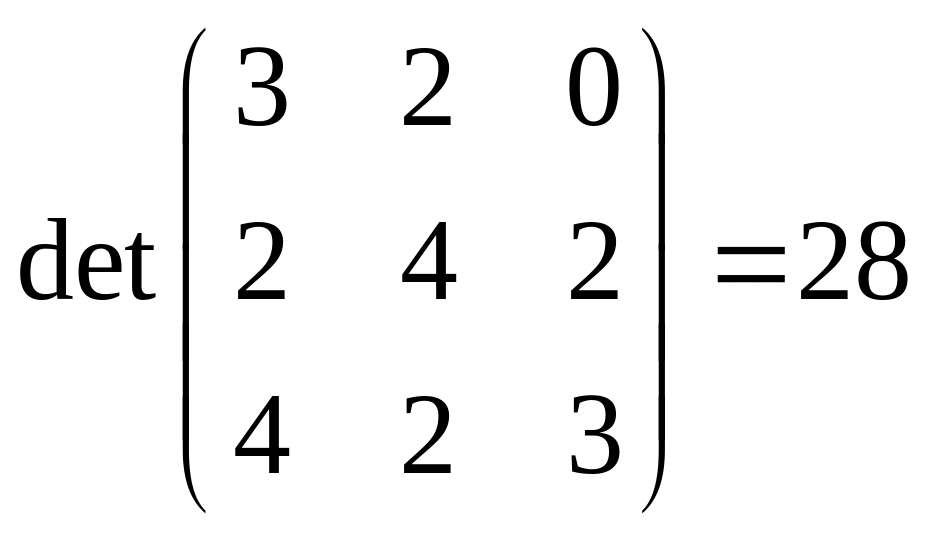Отже, .

Вiдповiдь. .