4.2. Обчислення визначника за методом Гаусса

Цей метод полягає в тому, що за допомогою елементарних перетворень рядків (чи стовпчиків) початкова матриця зводиться до вигляду матриці, визначник якої обчислюється просто, тобто до одиничної, діагональної, трикутної (верхньої чи нижньої) матриці, або до матриці, що має нульовий рядок чи стовпчик. При цьому елементарні перетворення вигляду 1) або 8) можна робити без жодних обмежень, елементарні перетворення вигляду 2) трансформуються в правило винесення спільного множника рядка або стовпчика з-під знака визначника, а при здійсненні елементарних перетворень вигляду 6) слід пам'ятати, що визначник при цьому змінює знак. За такого зведення можемо використовувати усі методи та технічні прийоми, які звичайно використовуються при застосуванні елементарних перетворень матриць.

Приклад.

.

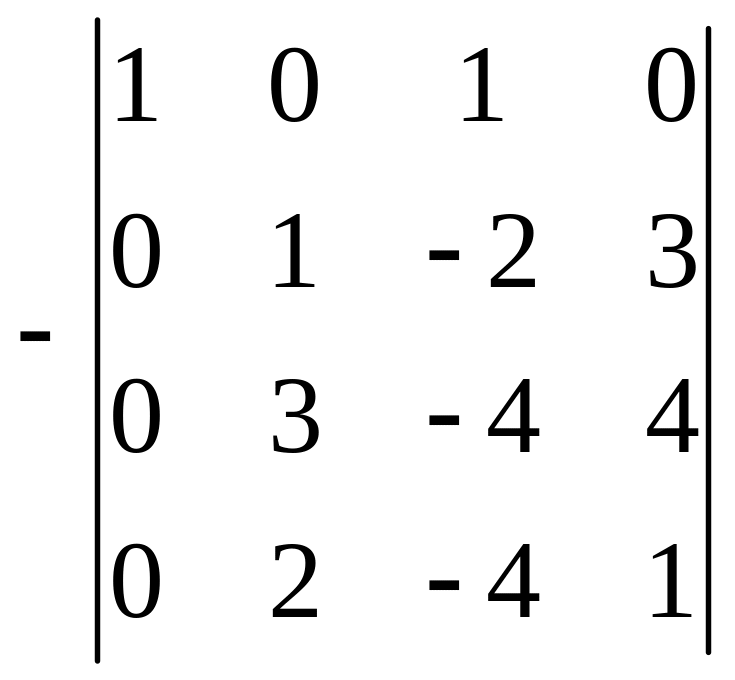
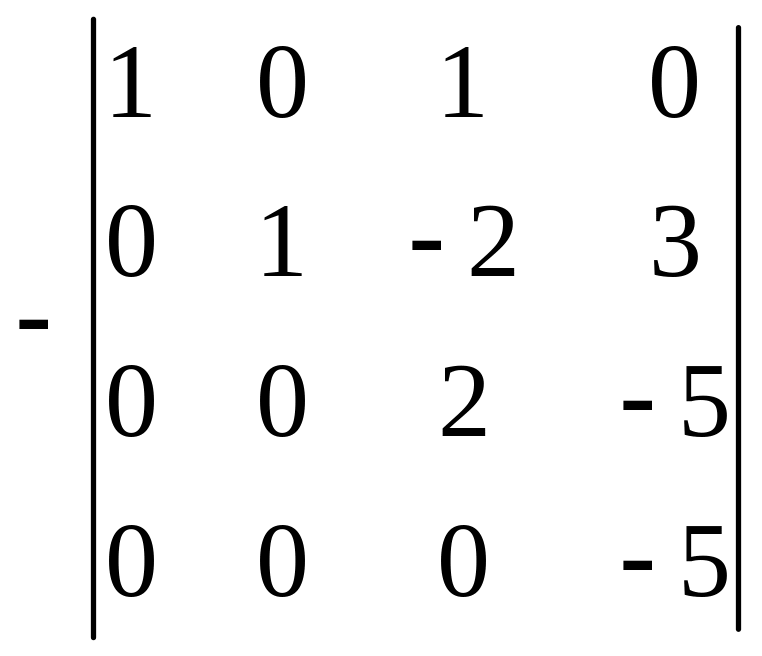
4.3. Пiдстановки та перестановки

Означення. Перестановкою на скiнченiй множинi називається розмiщення елементiв множини у певному порядку.

Приклад. Нехай множина складається з трьох символiв , Тодi з елементiв цiєї множини можна утворити шість перестановок:

Усі вони є абсолютно рiвноцiнними з погляду теорії.

Надалi розглядатимемо перестановки вiдрiзка натурального ряду, тобто множини

.

На цiй множинi iснує природний порядок розмiщення елементiв: вiд найменшого, тобто 1, до найбiльшого –  – у порядку зростання.

Означення. Нехай є деяка перестановка множини . Iнверсiєю в перестановцi називається пара , така що i

Приклад. Нехай У перестановцi мiстяться такi iнверсiї : В перестановцi мiстяться iнверсiї .

Iнверсiї iнколи ще називають безпорядками, щоб пiдкреслити: iнверсiя означає, що пара елементiв у перестановцi "йдуть не по порядку".

Означення. Перестановка множини називається парною, якщо кiлькiсть iнверсiй у нiй є парною. Перестановка множини називається непарною, якщо кiлькiсть iнверсiй у нiй є непарною.

Приклади. 1. Перестановка є парною, тому що вона мiстить парну кiлькiсть iнверсiй - Ось цi iнверсiї :

2. При на множинi iснує тiльки одна перестановка , i вона, очевидно, є парною (iнверсiй немає, тому що немає чим ї х утворювати).

3. При iснують двi перестановки: парна та непарна .

Факт. Кiлькiсть перестановок на множинi дорiвнює .

Факт. Єдина перестановка на множинi , що містить iнверсiй, є .

Означення. Пiдстановкою на множинi називається взаємно однозначне вiдображення множини в себе. Тотожне вiдображення множини в себе називається одиничною пiдстановкою i позначається або ж просто , коли вiдомо, про яку множину йдеться.

Одинична пiдстановка є, звичайно, парною, тому що вона мiстить iнверсiй.

Приклад. Знову розглянемо множину , що складається з трьох символiв Тодi вiдображення , , , не є взаємно однозначним, тому що два елементи переходять в один. Відображення , , , є взаємно однозначним, отже, є пiдстановкою.

Якщо та – два взаємно однозначних вiдображення, тодi їх суперпозицiя теж є взаємно однозначним вiдображенням. Вважається в запису суперпозицiї , що спочатку дiє перша справа пiдстановка: у випадку спочатку дiє , а потiм , або для . Суперпозицiю двох вiдображень часто називають їх добутком. Отже, ми теж будемо говорити про добуток пiдстановок, маючи на увазi при цьому ї х суперпозицiю.

Табличний запис пiдстановок

Кожне вiдображення можна записати у виглядi таблицi з двома рядками: у першому записуються в деякому порядку елементи множини , у другому ж пiд кожним елементом записуємо елемент .

Приклад. Так, вiдображення з попереднього прикладу запишеться у виглядi , а пiдстановка – як . Елементи у першому рядку можна записати в довiльному порядку, наприклад, три таблицi

, ,

визначають одну й ту саму пiдстановку.

Якщо пiдстановка визначена на множинi , то для пiдстановки зручно записувати її перший рядок у природному порядку: . Отже, пiдстановка , така, в якій , , , буде записана у виглядi . Iншi еквiвалентнi записи, наприклад , зустрiчається рiдко.

Множина усіх підстановок на множині позначається .

Множення пiдстановок, заданих у виглядi таблиць

Нехай , - двi пiдстановки, визначенi на множинi . Щоб обчислити :

1) записуємо пiдстановку у виглядi таблицi з двох рядкiв;

2) пiд кожним елементом , записаним у другому рядку цiєї таблицi, записуємо значення ; у результатi одержуємо ще один, третiй рядок;

3) таблиця, утворена першим та третiм рядками, є таблиця, що вiдповiдає добутку – пiд кожним з першого рядка в третьому рядку є записаним вiдповiдне значення .

Приклад. Нехай ,

, .

Використаємо сформульоване вище правило для обчислення .

.

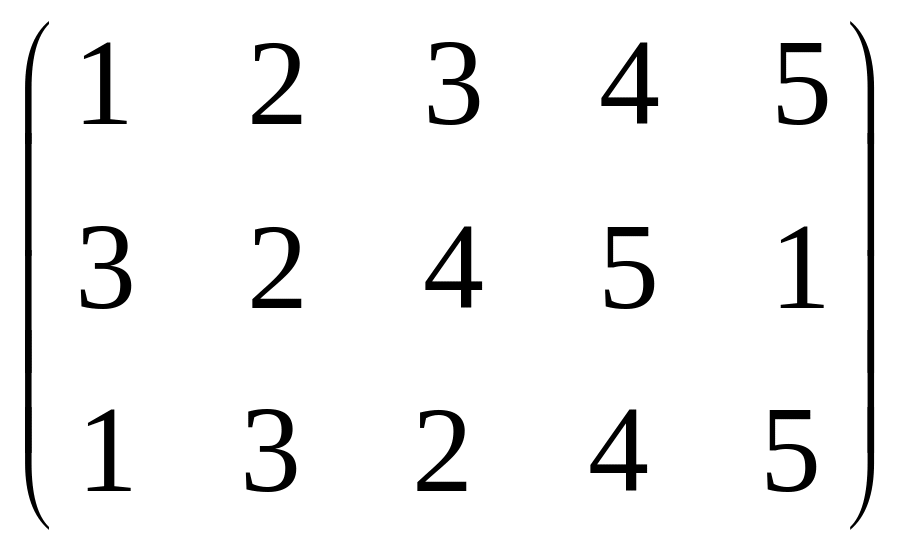Перший та третiй стовпчики утворюють таблицю пiдстановки :

.

Означення. Пiдстановка називається транспозицiєю, якщо iснують два елементи , такi що , , , а також для . Це означає, що ця транспозицiя переставляє елементи та .

Транспозицiю, що переставляє мiж собою елементи та , позначатимемо .

Приклад. Пiдстановки

, ,

є транспозицiями.

Зауваження. Для довiльної транспозицiї виконується рiвнiсть . Дiйсно, припустимо, що переставляє мiсцями та , . Тодi для , маємо , отже, ₌ . Нам залишилось перевiрити рiвнiсть, яку доводимо, для значень та . Згiдно з визначенням , . Рiвнiсть перевiряється аналогiчно.

Дуже важливим є такий факт:

Факт. Довiльна пiдстановка може бути зображена як добуток транспозицій .

Зауважимо, що такий розклад не є однозначним.

Наведемо спосіб розв'язування цiєї задачi. Дiятимемо так: побудуємо ланцюжок пiдстановок такий, що кожна пiдстановка , є транспозицiєю або ж тотожною пiдстановкою i, крiм того, має мiсце рiвнiсть . Домножуючи цю рiвнiсть на злiва, одержимо i оскiльки , то маємо . Аналогiчно, домножуючи останню рiвнiсть на злiва i враховуючи, що , маємо . Повторюючи цю операцiю для , одержуємо , чим і завершується розв'язання задачі. Ланцюжок будуємо індукцією за кількістю інверсій. Достатньо показати як знайти транспозицію таку, що має кількість інверсій меншу від кількості інверсій . Нехай  – останній рядок підстановки . Якщо не є тотожною підстановкою, то існує індекс такий, що . Тоді транспозиція є шуканою (у підстановці інверсія, яку утворювали та зникла, а решта збереглися).

Парнi та непарнi пiдстановки

Дамо два рiвносильнi визначення важливого поняття парностi пiдстановки. Кожне з визначень має свої переваги та недолiки. При розв'язаннi задач використовуємо те визначення, яке здається бiльш зручним для розв'язання саме цiєї задачi.

Означення 1. Нехай є пiдстановка на множинi , записана в табличному виглядi, причому у верхньому рядку елементи розмiщенi в порядку зростання. Пiдстановка називається парною, якщо перестановка , утворена елементами нижнього рядка, є парною (тобто перестановка мiстить парну кiлькiсть iнверсiй). Пiдстановка називається непарною, якщо перестановка , утворена елементами нижнього рядка, є непарною (тобто перестановка мiстить непарну кiлькiсть iнверсiй).

Означення 2. Нехай пiдстановка розкладена в добуток транспозицiй, . Пiдстановка є парною, коли число є парним i непарною, коли число є непарним.

Зауваження. Це визначення має двi особливостi.

1) Воно еквiвалентно попередньому визначенню.

2) Розклад пiдстановки в добуток транспозицiй не є однозначним, бiльш того, число залежить вiд цього розкладу. Незважаючи на це, парнiсть числа вiд цього розкладу не залежить.