
- •Предисловие
- •1. Воспитание – «тихое исцеление»
- •Следствия для педагогической практики до 9 года жизни ребенка
- •Практические аспекты воспитания детей и дошкольников
- •Аспекты воспитания в школьном возрасте и до 15 лет
- •Аспекты воспитания в подростковом возрасте:
- •Деятельность органов чувств – Переживание себя – Осознание себя – Духовный опыт
- •Чувства, которые дают возможность приобрести опыт переживания собственного тела:
- •Органы чувств, которые помогают получить опыт переживания окружающего мира на душевном уровне.
- •Органы чувств, служащие для душевно–духовного восприятия и переживания себя.
- •Жизнь тела и мыслительная жизнь – метаморфоза сил роста и регенерации в мыслительную деятельность
- •Законы судьбы в воспитании и биографическом развитии
- •2. Развитие в картинках
- •3. Здоровое расписание уроков: «всему свое время»
- •4. Салютогенетическое воспитание маленького ребенка и дошкольника
- •Детство в опасности
- •История и развитие Вальдорфскнх детских садов и Международной ассоциации вальдорфских детских садов
- •Практическое использование результатов исследования стрессоустойчивости и салютогенеза
- •От игры к чувству когерентности
- •Как дети учатся понимать мир
- •Формирование навыков и умений
- •5. О практическом применении вальдорфской педагогики
- •1. Как мне набирать материал для следующего класса, для следующего года обучения? Когда начинать, как собирать литературу?
- •2. Как выглядит внутренняя подготовка?
- •3. Как мне полюбить детей, в особенности «трудных»?
- •4. К чему следует стремиться, и что реально можно сделать за один учебный год?
- •5. Что может помочь научиться спокойствию?
- •6. Как установить конструктивные отношения с коллегами?
- •7. Благодаря чему происходит «образование чаши», о которой говорит Рудольф Штайнер в первом докладе общего человековедения?
- •8. Как мне сохранить увлеченность профессией?
- •9. Как мне создать духовную связь со своими учениками?
- •10. Может ли самоуправление улучшить деятельность учителей и насколько можно сочетать самоуправление с преподавательской деятельностью?
- •11. Может ли медитация улучшить мою работу? Если да, то с чего начинать?
- •12. Как мобилизовать силы здоровья, как раскрыть так называемые салютогенетические ресурсы?
- •13. Сколько нужно спать, чтобы оставаться здоровым
- •14. Стимулировать или ожидать, где критерии?! Сколько нужно ждать и как не упустить правильный момент?
- •15. По поводу дополнительных занятий: с какого возраста их проводить?
- •16. Какие методики помогают обучиться счету?
- •17. Раннее развитие
- •19. Что делать, если седьмой или восьмой класс больше не хочет петь? Следует ли посвятить этому время в пятом и шестом классе, и исключить пение в седьмом и восьмом классе?
- •6. Физиология учебного плана: Соответствующий возрасту детей материал урока и терапевтически действенная дидактика
- •О противоположности образа и музыки.
- •Какое действие на ребенка оказывают география – арифметика – геометрия?
- •Арифметика и геометрия
- •7. Проективная геометрия как путь к целостному пониманию пространства
- •Эпохи развития геометрии
- •1. Пирамиды как свидетели мистериальной мудрости древних времен51
- •2. Пентаграмма, число g золотого сечения и четыре фундаментальных вывода, связанных с ним
- •Четыре фундаментальных вывода в связи с числом g
- •3. Перспектива и новое осознание пространства
- •4. Открытие и изучение проективной геометрии – прорыв в пространственное сознание, не зависимое от чувственного восприятия
- •Как обращаться с удаленными элементами
- •Расширение понятий «внутри» и «снаружи»
- •О понятиях большое и малое
- •Мыслить одно и то же различными способами
- •Рассмотрение целостных объектов
- •Комплементарные кривые с их специфическими особенностями
- •Противоположные друг другу формы кривых
- •Еще раз о том же, но по-другому
- •Заключение
- •8. Профессиональная этика и духовная позиция в профессии воспитателя
- •Семь условий этического отношения Первое условие:
- •Второе условие:
- •Третье условие:
- •Четвертое условие:
- •Пятое условие:
- •Шестое условие:
- •Седьмое условие:
- •9. Медитация и образование сообщества
- •10. Две медитации для учителей и отношение к ученикам
- •11. Семь добродетелей искусства воспитания
- •12. Помощь в школьной повседневности
- •Умение обращаться с воспоминаниями
- •Отношения с классом
- •О наказаниях
- •Темперамент и качество жизни
- •13. Как долго длится время классного учителя?
- •14. Медико–педагогическая диагностика и терапия а) о профессиональном образе школьного врача
- •Консультации школьного врача, обследование в течение учебного года и обследование классов
- •Специфика школьной врачебной диагностики и терапии
- •Инкарнация в физический организм: большеголовость и малоголовость.
- •«Земные» и «космические» дети
- •Дети с «богатой» и «бедной» фантазией
- •Изучение учебного плана как инструмента помощи в душевном развитии
- •Выступления (при необходимости) на родительских собраниях по вопросам развития Работа над созданием доверительного отношения со стороны школьников
- •B) Рассмотрение детей на конференции. Кристоф Вихерт
- •С) Высокоодаренные дети. Михаэла Глёклер
- •D) Вспомогательный класс Карла Шуберта. Райноуд Энгельсман
- •Дополняющий подход лечебно–педагогического класса и его актуальность
- •Положение лечебно–педагогического класса в общей концепции вальдорфской школы
- •Содержание, форма и характер лечебно–педагогического класса
- •Е) Примеры лечебно–педагогических инициатив. Ингрид Рурманн, Бернд Руф, Михаэль Бирнталер Опыт практики Института Бернхарда Ливехуда
- •Шаги составления плана помощи в развитии
- •Коллегиальное сотрудничество в планировании помощи как управление качеством работы
- •15. Духовность в науке, искусстве и религии
- •А) о науке
- •Не сердце движет кровь, но кровь – сердце. Ойген Колиско.
- •B) о художественной деятельности – Опыт элементарной лепки в первых трех классах131. Хелла Лёве.
- •– Об обращении с языком и словом132. Барбара Деанжан фон Стрюк.
- •– Почему эвритмия? Улрике Вендт, Хелга Даниел.
- •– О методике познания человека в пластическом, музыкальном и речевом аспектах. Рудольф Штайнер133
- •С) о религии – религиозные качества в воспитании. Элизабет фон Кюгельхен.
- •16. Практикующее духовное человековедение
- •А) Дети и техника. Михаэла Глёклер137.
- •B) Ребенок и наркотики. Михаэла Глёклер
- •С) Дети и телевизор, компьютерные игры и комиксы. Михаэла Глёклер
- •Дети, воспитанные без телевизора, являются более здоровыми141
- •Помощь из Америки142
- •Компьютерные игры тоже не безобидны
- •Комиксы и мир картинок
- •Почему люди так много смотрят мультфильмы и читают комиксы?
- •D) Задачи воспитания в пубертетном возрасте. Кристоф Вихерт
- •Е) Вопросы, связанные с сексуальностью и половым воспитанием. Михаэла Глёклер
- •Гомосексуальность
- •Сексуальность и идентичность
- •Сексуальные извращения
- •17. Области совместной работы с родителями и учениками
- •Развитие понимания в отношении вальдорфской педагогики
- •В центре – индивидуальный ребенок
- •Пространства инициативы для родителей
- •Решение конфликтов
- •Участие родителей в различных фазах развития школы
- •Сотрудничество со школьниками
- •Разговаривать с учеником, а не о нем
- •Взятие на себя педагогической ответственности
- •18. Учительская коллегия как рабочее сообщество, отвечающее за руководство школой
- •А) Духовные аспекты
- •B) Правовые аспекты
- •С) Экономически–социальные аспекты
- •Осознание порога в социальной жизни
- •Жизнь и деятельность Карла Шуберта
- •Жизнь и деятельность Ойгена Колиско
- •Приложение
- •II). Результаты исследований, которые показывают оздоравливающее воздействие вальдорфской педагогики
- •1) Вальдорфские школьники являются более здоровыми
- •2) Влияет ли возраст начала школьного обучения на успеваемость и школьные достижения?
- •3) Отчет о научном исследовании parsifal
- •4) Антропософский образ жизни положительно воздействует на кишечную флору у детей
- •Адреса и ссылки Вальдорфская педагогика Рудольфа Штайнера
- •Антропософская медицина
- •Образовательные учреждения:
- •Правовые вопросы
- •Контакты:
- •Первоисточники
Еще раз о том же, но по-другому
Сначала зададимся вопросом: что такое тип кривой? Мы говорим о кривых одного и того же типа в том случае, если им присущи одни и те же сингулярности, и причем в одинаковом количестве. Всем, изображенным на рис. 29a–f кривым, присущи одни и те же особенности: касательная в точке перегиба w и точка самопересечения D. На рис. 29а это можно увидеть непосредственно. Кривые на рис. 29b–f могут, однако, просто проходить каждая в своей целостности. Необходима некоторая тренировка в том, чтобы распознать их принадлежность к одному и тому же типу. Причина в том, что некоторые элементы кривых (как минимум определенные сингулярности) выступают в роли удаленных элементов. Обозначенные стрелочками направления задают каждый раз две возможности для прохождения кривой. Они задают т.н. направление прохождения и требуют от наблюдателя навыка распознавать целостность кривой, проходящей через бесконечность. Подобный способ рассмотрения подводит к границе начальных имагинативных способностей. Если сравнить эти рассмотрения с наблюдением конфигурации Дезарга, обращает на себя внимание то, что одна и та же конфигурация может рассматриваться различными способами, а у шести различных кривых можно найти одни и те же элементы в измененной форме. Это удается с помощью упомянутой имагинативной способности, которую можно развить на вышеописанном геометрическом пути. Также очевидным является то, что на этом пути развивается способность распознавать типы в растительном и животном мире, а также их систематизировать. Ведь в основе всей эволюции находятся законы математики и геометрии. То, что «боги занимаются геометрией», было известно в древних мистериях. Человек может распознать в себе эту божественную мудрость и научиться с ней обращаться. В связи с этим Рудольф Штайнер написал примечательные строки в письме к графу Польцеру–Ходитцу: «Когда молодой человек изучает математику, в нем рождается божественное дитя». Это божественное дитя, эту чисто имагинативную способность, следует развивать. Но эта присущая чистому математическому мышлению способность может потускнеть или вовсе утратиться, если использовать математику и геометрию, не познавая их чистого источника. Познание самого себя в процессе творческого подражания и освоения этих чистых мыслительных форм относится к центральным задачам духовного самопознания.
-

Рисунок 29а
Рисунок 29b

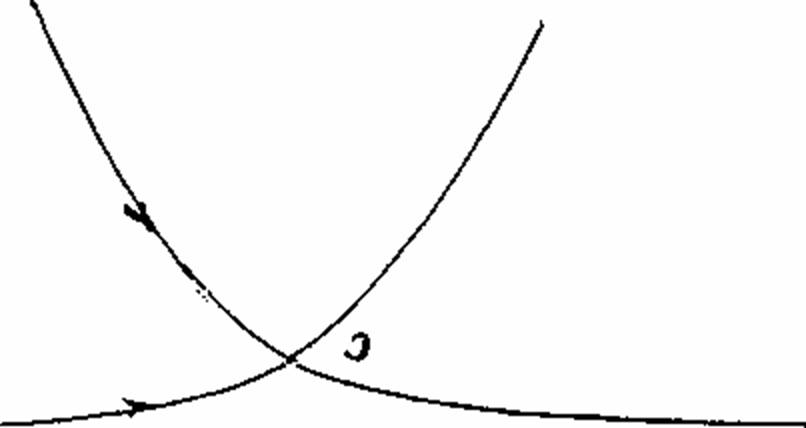
Рисунок 29c
Рисунок 29d
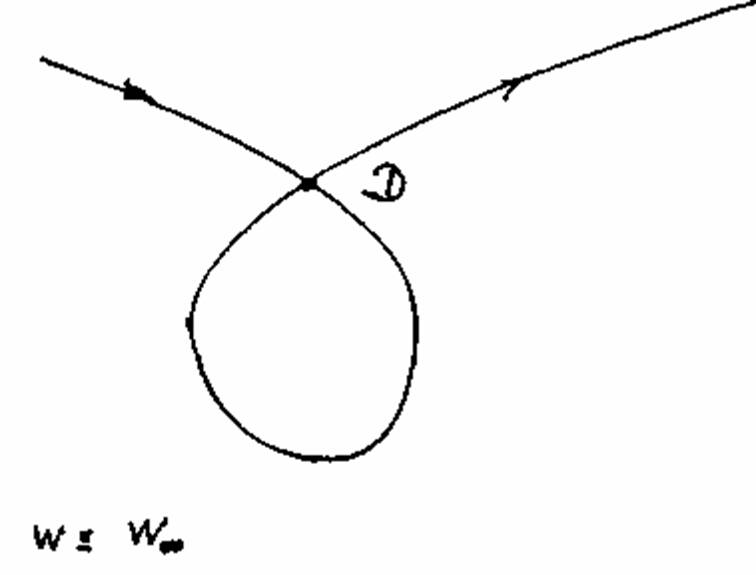
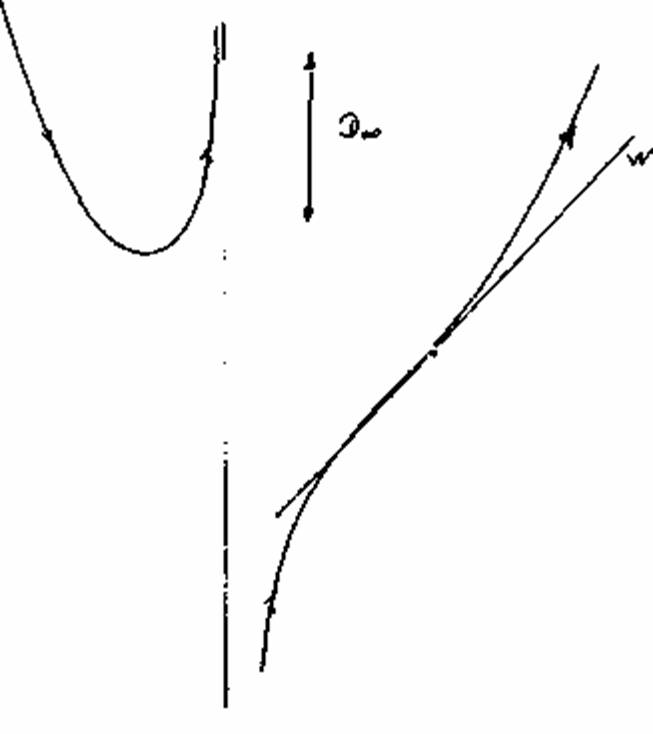
Рисунок 29e
Рисунок 29f
Заключение
Абстрактное рассмотрение целесообразно в том случае, когда требуется детально осмыслить особенности или подробности большого целого: специфическую сингулярность какой-либо кривой, отдельный листок дуба, печень как человеческий орган и т.д. Но при этом всегда следует помнить о том, что таковые детали являются в этом случае изолированными единицами вышестоящего целого. Пространство как идея являет собой пример такого вышестоящего целого. Этот факт можно осмыслить лишь путем пошаговых упражнений. Вот элементарный пример этому:
На концах ограниченного горизонтального отрезка находятся две точки А и В. Прямая g проходит через эти точки, но продолжается направо и налево в бесконечность. При этом точка, двигающаяся налево все более удаляется от точки, смещающейся вправо.
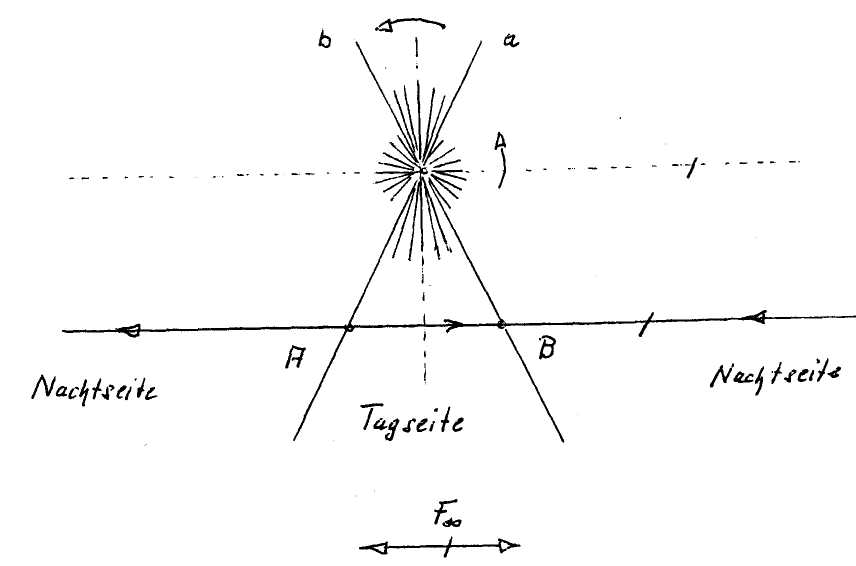
Находящаяся справа, бесконечно удаленная точка F∞ тождественна находящейся слева. Двойная стрелка символически выражает этот факт.
Благодаря проективной геометрии эти на первый взгляд кажущиеся противоположно направленными движения могут рассматриваться как направленные навстречу друг другу. Так как обе двигающиеся точки встречаются в удаленной точке F∞ прямой g. Другими словами: конечный отрезок AB проходит на дневной стороне, а «бесконечный отрезок» AB находится на ночной стороне. Таком образом мы познаем прямую g в целом.
Какое значение для человека может иметь подобное расширение сознания? Ответом на этот вопрос может служить пример из жизни молодого Рудольфа Штайнера:70
«...Одно важное переживание пришло ко мне из области математики. Мне доставляло самые большие внутренние сложности представление пространства. Его сложно было мысленно представить как уходящую в бесконечность пустоту, каким его описывали господствующие тогда естественно–научные теории. Благодаря новой (синтетической) геометрии, с которой я познакомился на лекциях и частных уроках, в моей душе родилось представление, что линия, продолженная вправо в бесконечность, возвращается слева к исходной точке. Находящаяся справа бесконечно удаленная точка совпадает с находящейся слева бесконечно удаленной точкой. Мне пришло на ум, что с помощью таких представлений новой геометрии можно достигнуть понятийного познания уходящего в пустоту пространства. Для меня было настоящим откровением представление о возвращающейся к себе, словно линия круга, прямой. Я возвращался с лекции, на которой это представление впервые родилось в моей душе, и чувствовал, будто с меня свалился огромный груз. Меня охватило освобождающее чувство. Опять, как в мои отроческие годы, геометрия одарила меня ощущением счастья...».
