Относительность движения

Для описания движения необходимо выбрать систему отсчета. В ряде задач приходится рассматривать движение одного и того же тела относительно разных тел, причем эти тела, а следовательно, связанные с ними системы отсчета, могут двигаться друг относительно друга.

Если известна скорость тела в движущейся системе отсчета со скоростью, называемой относительной скоростью , и известна скорость подвижной системы относительно неподвижной со скоростью, называемой переносной , то скорость тела относительно неподвижной системы отсчета, абсолютная скорость – , определяется согласно классическому закону сложения скоростей:

= + ,

Т.е. абсолютная скорость тела равна векторной сумме относительной и переносной скоростей.

Обратим внимание на то, что взяв производную по времени от левой и правой частей этого равенства, мы получим выражение для мгновенного ускорения.

Если же тела, с которыми связаны неподвижная и подвижная системы отсчета движутся равномерно друг относительно друга и одна из систем является инерциальной (см. ниже), то ускорения тела равны:

=

1.3. Ускорение

Величина, характеризующая быстроту изменения скорости, называется ускорением.

Среднее ускорение – величина, равная отношению изменения скорости к промежутку времени, за который это изменение произошло:

= /Δt. (1.10)

Если и – мгновенные скорости в моменты времени t₁ и t₂, то

= – , Δt = t₂ – t₁.

На рис.1.8 изображены векторы мгновенных скоростей. Чтобы их сравнить, сделаем параллельный перенос вектора в точку А. Тогда определит направление .

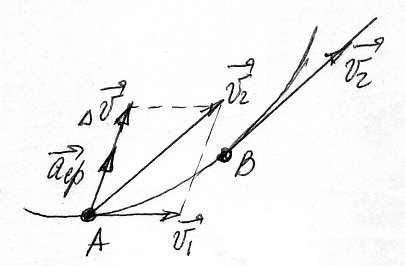
Рис. 1.8

Мгновенное ускорение – ускорение тела в данный момент времени. Это физическая величина, равная пределу отношения изменения скорости к промежутку времени, за который это изменение произошло, при стремлении промежутка времени к нулю:

= . (1.11)

Вектор направлен так же, как и вектор при Δt  0, и не совпадает в общем случае с направлением вектора скорости .

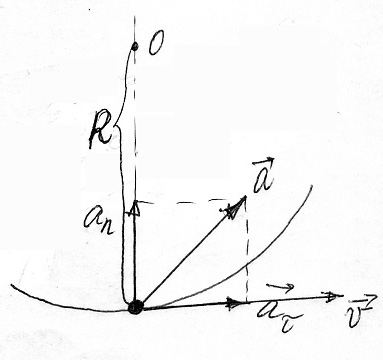
Рис. 1.9

Пусть вектор мгновенного ускорения направлен, как указано на рис.1.9, под углом к вектору скорости. Ускорение характеризует изменение скорости по модулю и по направлению. Разложим ускорение на две составляющие: а_ – тангенциальное (касательное) ускорение и а_n – нормальное (центростремительное) ускорение. Компонента а_ направлена по касательной к траектории и характеризует изменение скорости по модулю, а_n направлено к центру кривизны траектории (по нормали к скорости) и характеризует изменение скорости по направлению. Компонента а_n = v²/R, где – мгновенная скорость, R – радиус кривизны траектории в данной точке,

= + . (1.12)

Модуль мгновенного ускорения равен

а_мгн = . (1.13) При прямолинейном движении a_n = 0, скорость не изменяется по направлению. Если = остается постоянным, то материальная точка движется прямолинейно и равноускоренно. В этом случае среднее ускорение равно мгновенному:

= .

Из определения ускорения следует _{, (1.14)}

Направим ось ОХ вдоль направления движения тела в момент времени t = 0 (рис.1.10). Из определения ускорения следует

a_x = ,

где v_0x – скорость тела при t = 0.

Тогда v_x = v_0x + a_xt. _(1.12)

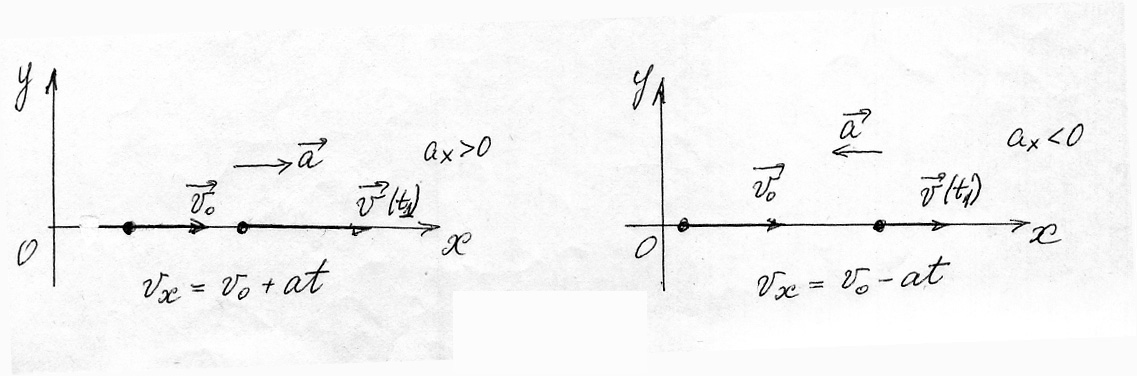
На рис.1.10 показаны различные направления ускорения.

П роинтегрировав v_x (t) по времени найдем уравнение прямолинейного равноускоренного движения:

_(1.15)

В векторном виде уравнение движения имеет вид:

(1.16)

Чаще при решении задач пользуемся уравнениями:

х = х₀  v₀t  at²/2,

v_x = v₀  at, (1.17)

где v₀ и a – модули начальной скорости и ускорения.