4. Динаміка кристалічних решіток

4.1. Поняття про нормальні коливання

Описана раніше структура кристалу є ідеалізованим випадком, коли всі атоми нерухомо "стоять" у відповідних вузлах кристалічної решітки. Строго кажучи, ця ситуація неможлива навіть при температурі близькій до абсолютного нуля завдяки співвідношенням Гейзенберга. (Якби координати атомів були строго визначені, вони не могли б знаходитися у спокої, тому що невизначеність їх імпульсів прямувала б до нескінченності.) Як і все ідеальне, ідеальний кристал - це лише модель. Атоми в кристалі рухаються як завдяки квантовим властивостям, так і завдяки тепловій енергії. Останній фактор є домінуючим при кімнатній та більш високих температурах. Рух атомів у кристалі є коливним, але він "хитріший", ніж, скажімо, коливання маятника. Подібно тому, як одна і та ж людина є одночасно пішоходом, платником податків, виборцем, глядачем, споживачем і т.і., атом одночасно бере участь у багатьох колективних рухах кристалу. Ці колективні рухи називають нормальними коливаннями.

Нормальні коливання - колективні коливання всіх частинок системи з однаковою (нормальною) частотою.

Будь-яка система, яка виведена зі стану рівноваги таким чином, що зміщення всіх складових частин малі, здійснює коливання, які є сукупністю нормальних коливань. Тобто зміщення кожного атома е суперпозицією гармонічних нормальних коливань з нормальними частотами (нормальні частоти знаходяться з секулярного рівняння класичної механіки).

Тепловий рух в кристалах можна уявити як накладання багатьох нормальних коливань з випадковими амплітудами та фазами.

Нормальні коливання в кристалі - це пружні хвилі.

4.2. Модель одноатомного ланцюжка

Розглянемо найпростішу модель, що складається з N атомів масою т, зв'язаних пружинками (для реального кристалу атоми відповідають атомним площинам, а пружинки -квазіпружним зв'язкам між площинами при малих зміщеннях). Атоми розмістимо у вигляді ланцюжка, на який накладемо граничні періодичні умови Борна-Кармана - останній атом замкнутий на перший (рис.4.2.1), - коефіцієнт жорсткості пружинок, а - відстань між рівноважними вузлами ланцюжка.

Запишемо динамічні рівняння для атомів ланцюжка. Координати кожного з атомів визначаються формулою

де - положення п -го атома в незбуреному ланцюжку, - зміщення (як правило, ).

Тоді для кожного атома рівняння руху матиме вигляд

де - потенціальна енергія системи, - сила, яка діє на п-й атом.

Величина V в даній моделі є сумою потенціальних енергій пружинок, в якій лише два доданки явно залежать від зміщення п -го атома. Тому

Таким чином, коливання одноатомного ланцюжка описується N диференціальними рівняннями типу

(*)

Розглядаючи як кінцеву різницю другого порядку, праву частину рівняння можна наближено подати у вигляді другої похідної по координаті

(**)

Отримали хвильове рівняння, яке описує поширення плоскої хвилі в неперервному середовищі. Звичайно, цим наближеним рівнянням можна користуватися лише для хвиль, довжина яких набагато більша за міжатомну відстань.

Позначивши отримаємо рівняння -яке має розв’язки , тобто рівняння плоскої хвилі. Цей результат для наближеного рівняння (**) підказує шукати розв'язки системи динамічних рівнянь (*) у вигляді

(***)

При підстановці цього виразу для в (*) маємо

випадок А=0 (абсолютний спокій) виключаємо.

Можна зробити висновок, що розв'язок (***) задовольняє

рівнянню (*) за умови

Розглянувши геометричну інтерпретацію (рис.4.2.2) одержаного закону дисперсії, бачимо, що інтервал є не що інше, як перша зона Бріллюена (комірка Вігнера-Зейтца оберненої решітки

Строго кажучи, величину k не можна вибирати довільно, Оскільки на систему систему накладені граничні умови Борна-Кармана,

Очевидно що в першій зоні Бріллюена шириною

реалізується N дозволених значень k

Величина k визначає проекцію хвильового вектора пружної хвилі на вісь х. Якщо хвиля має довжину , то

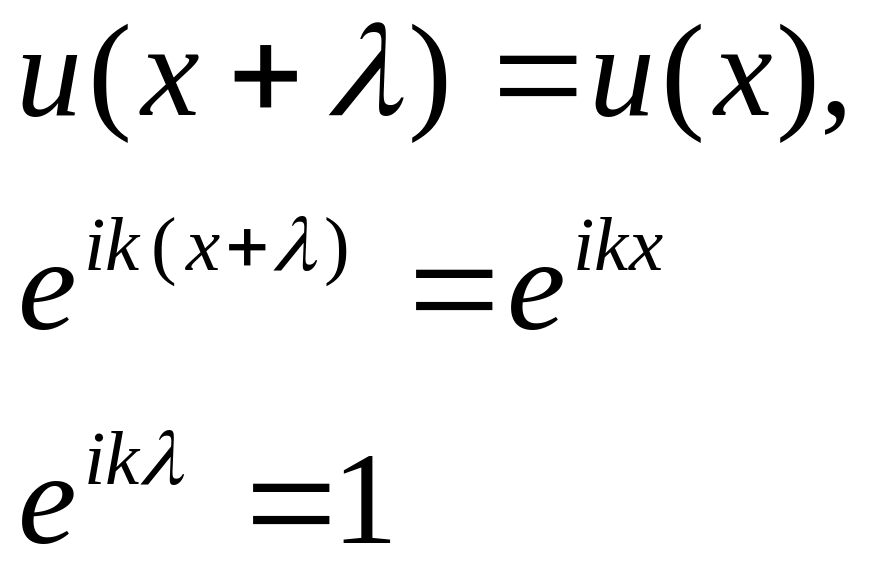
Отже, кратне

З іншого боку, якщо додати до хвильового вектора k період

оберненої решітки (або довільний вектор оберненої решітки й

то закон коливання будь-якого атома не змінюеться

Таким чином додавання до вектора k з першої зони Бріллюена довільного вектора оберненої решітки не змінює стану системи - У саму хвилю. Можна зробити висновок, що всі фізично різні коливальні стани решітки вичерпуються першою зоною Бріллюена.

З закону дисперсії пружних хвиль в ланцюжку можна а фазову та групову швидкість.

Фазова швидкість (швидкість руху фронту постійної фази)

Групова швидкість

Розглянемо два граничні випадки:

1)

у цьому випадку тобто це випадок довгих хвиль. Оскільки синус малого аргументу можна замінити значенням аргументу, то

причому можна розглядати як швидкість звуку.

Приведемо цей вираз до вигляду, в якому використовуються величини, що безпосередньо вимірюються в експерт Легко бачити, що коефіцієнт пружності в моделі ланцюжка зв'язаний з модулем Юнга співвідношенням р. . Дійсно, порівнюючи закон Гука для абсолютної деформації, і для відносної деформації, площа, що приходиться на один атом площини), приходимо до вказаного співвідношення. Масу атома можна виразити через густину і об'єм а комірки, що припадає на один атом. В результаті приходимо до відомого з курсу загальної фізики