2. Квантова теорія вільних електронів у металі

2.1. Електронний газ при . Сфера Фермі

Вільні електрони в металі можна розглядати як частинки в потенціальному ящику, які підкоряються стаціонарному рівнянню Шредінгера з відповідними граничними умовами:

Електрони в потенціальному ящику вважаються вільними, тому всередині металу . Для простоти розглянемо металевий зразок, як паралелепіпед.

Щоб описати стан електрона в металі, необхідно задати граничні умови. Макроскопічні властивості металу не залежать від конкретного вигляду граничних умов, тому їх вибирають із міркувань математичної зручності. Простий фізичний зміст мають такі граничні умови:

(ящик з нескінченно високими стінками)

Однак найчастіше користуються періодичними граничними умовами Борна-Кармана.

Спочатку знайдемо загальні розв'язки.

довільним розв'язком є , де напрям довільний, а

Подіємо на функцію оператором проекції імпульсу тобто Власне значення. Отже, хвильова функція описує квантовий стан електрона з імпульсом ( - хвильовий вектор), цьому імпульсу відповідає довжина хвилі Невизначеність координати , тоді маємо невизначеність імпульсу , цьому відповідає невизначеність хвильового вектора . Врахуємо граничні умови Борна-Кармана:

аналогічно

Граничні умови накладають обмеження на хвильовий вектор. Вони роблять спектр дискретним. Множину і дозволених станів електрона в металі зручно зображати векторами, або точками оберненого простору, який, називають к-простором. Всі дозволені стани системи електрона утворюють у к-просторі регулярну сітку вузлів із періодами

вздовж відповідних осей. Таким чином, на кожен вузол такої сітки припадає одна комірка у вигляді паралелепіпеда

зі сторонами тобто на кожен дозволений стан електрона приходиться об’єм

в к – просторі. В силу співвідношення Гейзенберга стан електрона

розмазаний по цій комірці. Згідно принципу Паулі в кожній комірці не може перебувати більше двох електронів. Розглянемо тепер електронний газ вільних і незалежних електронів «при абсолютному нулі» (тобто при достатньо низькій температурі). При кожен електрон намагається зайняти квантовий стан з найменшою енергією, тобто ближче до центру ^-простору, а відстанню до центра є хвильове число к, яке визначає енергію електрона В силу принципу Паулі електрони займають певний об'єм навколо центру k- простору вигляді кулі; границя цієї кулі називається сферою Фермі. Знайдемо радіус сфери загальна кількість електронів у металі, кількість заповнених комірок,

отже .

Енергія Фермі - це максимальна енергія електрона при абсолютному

нулі температури,

Швидкість Фермі м/с

Отже, навіть при рух не завмирає, електрони «гасають»

по металу з швидкостями під мільйон метрів за секунду. Причина цього - принцип Паулі.

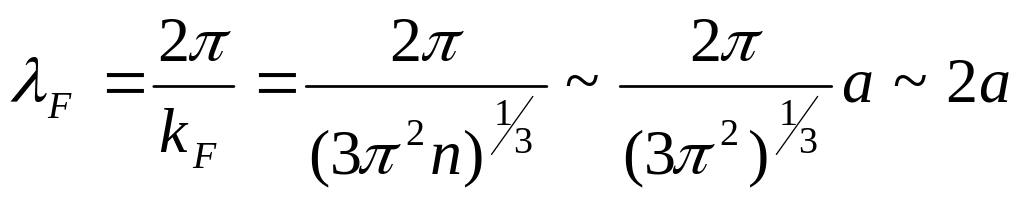
Отже, можна чекати дифракції електронів на решітці.

2.2. Електронний газ при ненульовій температурі. Теплоємність електронного газу. Уявлення про теорію Зоммерфельда

Температура електронного газу більша нуля, отже за рахунок теплових флуктуацій електрони можуть виходити зі сфери Фермі, тобто сфера розмивається і це розмиття описується розподілом Фермі-Дірака тоді енергія електронного газу

залежить від температури,

- густина станів, - кількість станів .з енергіями з інтервалу в яких можуть перебувати електрони. Енергія і хвильове число однозначно зв'язані, тому Якщо в оберненому просторі виділимо

прошарок товщиною dk і радіусом k, то кількість станів буде рівна

звідси

Повна енергія:

(1)

Аналогічно повна кількість електронів:

(2)

Ці два рівняння складають основу теорії Зоммерфельда, із рівняння (2) випливає, що при умові

Дж, Дж,

так що при будь-якій температурі (нижче плавлення) класичні властивості електронного газу вироджені.

Можна показати, що при умові виродженості електронного газу його енергія де нульовий рівень , знаходимо, використовуючи рівність (1):

Квадратичну залежність від температури для енергії виродженого газу можна зрозуміти з наступних міркувань. З ростом температури від абсолютного нуля, електрони отримують можливість виходити за межі сфери Фермі, набуваючи при цьому додаткової енергії порядку А:Г. Але цю можливість можуть використати лише ті електрони, які знаходяться поруч зі сферою Фермі, тобто, дія яких

. Кількість таких електронів по порядку величини рівна зміна енергії електронного газу

Раз енергія змінюється квадратично, то звідси теплоємність прямує до нуля по лінійному закону і при будь-яких реальних температурах для металу вона набагато менша ніж теплоємність класичного газу. Зоммерфельд показав, що в квантовій теорії вільних електронів можна використовувати результати класичної теорії, якщо в них зробити дві заміни:

В усіх процесах розсіювання електронів на дефектах приймають

участь лише електрони з тонкого прошарку навколо сфери Фермі з енергетичною товщиною порядку kT, тому всі ці електрони мають приблизно однакову швидкість рівну швидкості Фермі Наприклад, розглянемо теплопровідність металів. Згідно класичної теорії , тоді квантова теорія дає

В законі Ома ніяких змін не треба робити, тоді відношення теплопровідності до електропровідності матиме вигляд:

(Нагадаємо, що ). Квантова теорія дає узгодження з експериментом.

Модель вільних електронів у металі задовільно описує експериментальні дані лише для лужних металів, але навіть для них ця модель не узгоджується з даними ефекту Холла та оптичними властивостями металів. Крім того, теорія вільних електронів зовсім не пояснює залежність електричних властивостей твердих тіл від їхньої структури. Як було видно з оцінки довжини хвилі де-Бройля, для сфери Фермі, електрони повинні дифрагувати на власній кристалічній решітці, а значить не можна нехтувати взаємодією електронів з решіткою.