Розглянемо метал як електронний газ, який знаходиться в вакуумі. Тоді для вакууму

і

Візьмемо

Метал завжди залишається електронейтральним, через те , тому а оскільки то . Враховуючи що отримаємо наступне хвильове рівняння (с-швидкість світла в вакуумі).

Розглянемо електромагнітне поле, яке змінюється в часі за гармонічним законом , тоді локальна густина струму теж буде змінюватись за гармонічним законом: де Підставимо все це в отримане вище хвильове рівняння:

Отримаємо диференціальне рівняння для амплітуди і розглянемо лише випадок високочастотних коливань

-

квадрат плазм енної частоти

( — частота колективних коливань електронного газу).

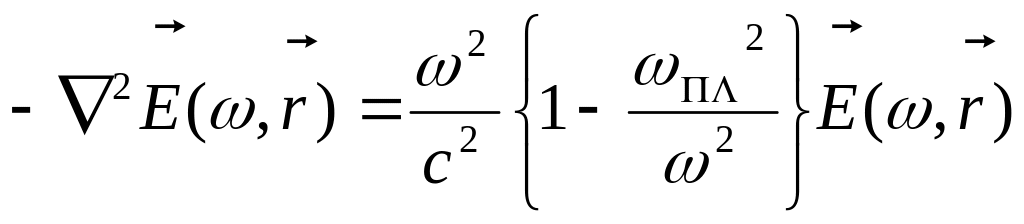
Нехай електромагнітна хвиля розповсюджується вздовж осі х,

вглиб металу .Розглянемо два випадки:

1) (порядка 10¹⁷ с^-1 і вище), тоді >0, тоді

.

Висновок: хвиля проходить через метал, тобто метал для неї прозорий (якщо нехтувати впливом іонної підсистеми).

2) тоді

розв'язком цього рівняння є Із фізичних міркувань ми можемо покласти, що В=0, бо енергія не може наростати при розповсюдженні хвилі вглиб металу, тоді

Характерна глибина затухання, тобто глибина, на якій поле зменшиться в е раз, буде

1.7. Теплопровідність металів. Закони Фур'є та Відемана - Франца

Закон Фур'є (закон теплопровідності): густина теплового потоку пропорційна градієнту температури і направлена від вищої температури до нижчої, коефіцієнт теплопровідності. Відомо, що метали проводять тепло краще, ніж інші речовини. Відеман і Франц показали, що відношення теплопровідності до електропровідності пропорційне Т, а коефіцієнт пропорційності майже однаковий для всіх металів (тепер

його називають числом Лоренца)

На основі припущень Друде-Лоренца знайдемо теплопровідність. Розглянемо металевий стержень і виділимо в ньому площину х.

Ми отримаємо перенесення енергії від правого кінця до лівого, бо праворуч електронам «гарячіше».

енергія, яку отримують електрони в точках л: • Множник означає, що після зіткнення половина електронів рухається праворуч, половина - ліворуч. залежить від х неявно, через температуру, тому

- квадрат проекції, енергія електрона. Звідси Знайдемо співвідношення між тепло- і електропровідністю за вище отриманими виразами

це і є число Лоренцо. Отже тобто класична теорія лише частково пояснює закон Відемана - Франца.

1.8. Ефект Зеебека

Ефект Зеебека - це один із термоелектричних ефектів, при якому градієнт температури породжує електричне поле

О,- коефіцієнт пропорційності, диференціальна термо- ЕРС. Електрони з гарячого кінця рухаються до холодного кінця з більшою середньою швидкістю, ніж навпаки. Тому на холодному кінці вони почнуть накопичуватись, «оголяючи плюси» на гарячому кінці. Це мусить привести до зростання різниці потенціалів і, відповідно, до виникнення електричного поля з силовими лініями, направленими від гарячого кінця до холодного. Це поле почне гальмувати швидкі електрони, що рухаються від гарячого до холодного, і прискорювати електрони в зворотньому напрямі. Зрештою мусить встановитись стаціонарний стан з нульовим середнім. потоком електронів. Умова стаціонарного стану після виникнення компенсуючого електричного поля за модулем:

місце , де електрон останній раз зіткнувся з іоном.

За модулем

Швидкість залежить через температуру від х, а не безпосередньо.

Врахуємо знаки термо – ЕРС

градієнт температури. - таку формулу можна використати в квантовій теорії.

Для всіх металів, згідно теорії Д - Л, термо - ЕРС повинна бути

однакова і від'ємна, що не узгоджується з експериментом. Вихід -врахувати квантові особливості.