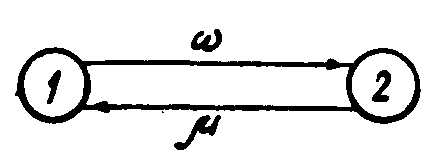3 Расчет характеристик безотказности восстанавливаемых систем

Основные показатели безотказности:

Наработка на отказ ; t_i - время между соседними отказами; n - число отказов.

Параметр потока отказов (t) = n (t)/N t; n (t)- число изделий, отказавших в интервале от ( t - 0,5 t) до ( t + 0,5 t) ; N - число испытанных изделий; t - интервал времени.

Коэффициент готовности К_г = t_ср /(t_ср + t_в); t_ср - наработка на отказ; t_в - среднее время восстановления.

Коэффициент технического использования К_т.и = t_ср /(t_ср + t_в + t_т.о); t_т.о -.время технического обслуживания.

Показатели безотказной работы позволяют проводить различные расчеты, в том числе расчет потребности в запасных частях.

Количество запасных частей n_з.ч =  t N

Для достаточно большой наработки (от t₁ до t₂ )

Пример 3.1. Интенсивность отказов изделия  = 0,02 1/ч; среднее время восстановления t_в = 10 ч. Вычислить коэффициент готовности К_г .

Р е ш е н и е. Средняя наработка до первого отказа

Т_ср = 1/ = 1/0,002 = 50 ч

Коэффициент готовности

К_г = Т_ср /(Т_ср + t_в) = 50/(50+10) = 0,83

	ПРИМЕР 5.2. Пусть необходимо определить надежность изделия, не имеющего резервирова- Ния, с заданными интенсивностями переходов – параметров потока отказов  = const, и интенсивностью восстановления .
Рис. 5.4

Работоспособность системы описывается графом (рис. 5.4): состояние 1 - состояние работоспособности, состояние 2 - состояние отказа.

Описание графа по приведенному правилу дает следующую систему уравнений вида (5.2):

Z P₁ (Z) - P₁ (0) = -P₁ (Z)  + P₂ (Z) ,

Z P₂ (Z) - P₂ (0) = P₁ (Z)  - P₂ (Z) .

Учитывая, что в момент включения t =0 система должна быть исправна: P₁ (0) = l, Р₂(0) = 0, получаем:

Z P₁ (Z) + P₁ (Z)  - P₂ (Z)  = 1,

Z P₂ (Z) + P₂ (Z)  - P₁ (Z)  = 0.

Отсюда

P₂ (Z) = P₁ (t) /(Z+),

P₁ (Z)= (Z+)/[Z(Z+ +)].

Обратное преобразование вероятности P₁(Z) требует приведения ее к табличному виду. Для этого умножим и разделим P₁(Z) на ( +):

P₁(Z)={(Z+)/[Z(Z++)]}{(+)/(+)}=

=[ (Z+ +)+ Z]/[Z(Z++)(+)],

P₁(Z)=(1/Z)[/ (+)]+[1/(Z++)][ /(+)].

Отсюда, учитывая, что 1/Z соответствует 1(t), а 1/(Z++) соответствует e^-(+)t , получаем:

P₁(t)= [/ (+)]+[/(+)] e^-(+)t .

Анализом полученного выражения устанавливаем, что P₁(t) при t   не может быть ниже величины /(+). Эта постоянная часть, и является стационарным коэффициентом готовности изделия:

 / (+)= (1/t_в )/[(1/t_в )+(1/t_ср )] = t_ср /(t_ср + t_в )= K_г .

Постоянная времени экспоненты Т_пэ = 1/(+.). Переходный процесс длится 34 Т_пэ, после чего наступает установившийся режим.

ПРИМЕР 5.3. Пусть  = 10^-2 1/ч, a  = 1 1/ч. Тогда

Т_пэ = 1/(1+ 10^-2)  1 ч.

Следовательно, переходный процесс длится 34 часа, а далее надежность системы определяется стационарным коэффициентом готовности

K_г = 1/(1+ 10^-2) = 0,99.

Задание на самостоятельную работу по расчету характеристик безотказности восстанавливаемых систем

Задача 3.1. Определить норматив технического обслуживания оборудования для которого известны коэффициент технического использования Kти = 0,87, интенсивность отказов изделия  = 0,4*10-6 1/ч и среднее время восстановления tв = 5 ч.