2 Расчет безотказности невосстанавливаемых систем при основном и резервном соединениях элементов
Расчетные формулы для расчета вероятности безотказной работы технической системы при основном соединении элементов, когда отказ технической системы наступает при отказе одного из элементов, имеют следующий вид:
(19)
или
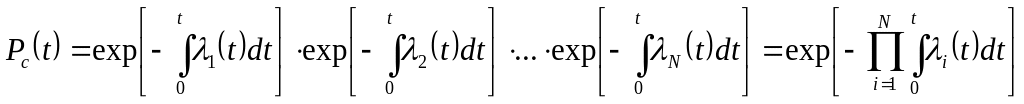
Если i= const и время возникновения отказов подчинено экспоненциальному закону распределения. Тогда количественные характеристики безотказности можно представить в виде
Pc(t)=exp [-c t]=exp [- t/Tср], c = i , аc(t) = c exp [-c t], Tср.с= 1/c (20)
Если все элементы рассматриваемого устройства равнонадежны, то
(21)
где Ni - число элементов i-го типа; r - число типов элементов.
Для высоконадежных систем, для которых t< 0,1, можно воспользоваться приближенными формулами, разложив ехр [-c t] в ряд и ограничиться первыми двумя членами, тогда
,
,
,
(22)
Поскольку
(23)
где Qi (t) = 1 - Pi (t) - вероятность отказа i-го элемента.
В невосстанавливаемых изделиях с резервным (параллельным) соединением элементов отказ одного из элементов не приводит к отказу системы в целом. Система откажет только тогда, когда откажут все элементы. Поскольку элементы независимы, то вероятность отказа системы
(24)
Вероятность безотказной работы системы
(25)
Среднее время безотказной работы системы
(26)
Пример 2.1. Определить вероятность безотказной работы системы из надежного ( P1 = 0,9) и ненадежного ( P2 = 0,4) элементов.
1. При основном соединении элементов
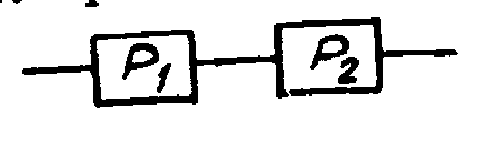
Pc = P1 P2 = 0,9 0,4 = 0,36
2. При резервном соединении элементов
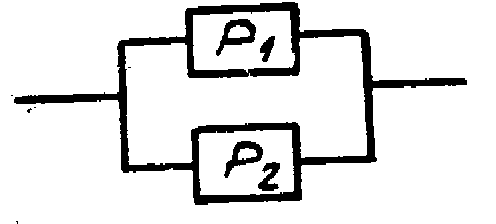
Pc = 1 - [(1-P1) (1-P2)] = 1 - [(1-0,9)(1-0,4)] = 0,94.
3. При резервном соединении двух надежных элементов
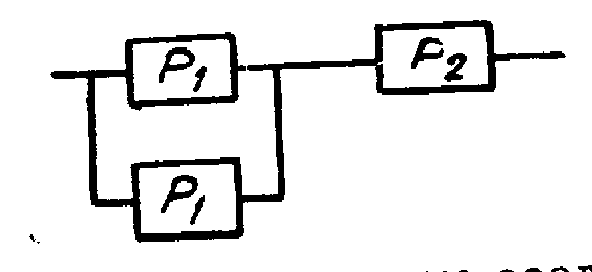
Pc = [1-(1-P1)2]P2 = [1(1-0,9)2]0,4 = 0,396.
4. При резервном соединении двух ненадежных элементов
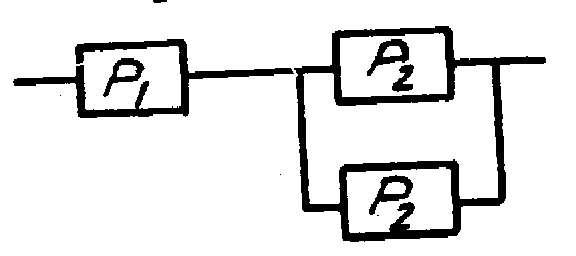
Pc = P1[1-(1-P2)2] = 0,9[1-(1-0,4)2] = 0,576.
Пример 2.2. В течение некоторого времени наблюдали за работой одного изделия. За весь период наблюдения зарегистрировано 10 отказов. До начала наблюдений изделие проработало 350 ч, к концу наблюдений наработка составила 2350 ч.
Определить среднюю наработку на отказ и интенсивность отказов, полагая справедливым экспоненциальный закон плотности распределения вероятности отказов.
Р е ш е н и е. Наработка изделия за период наблюдений
t = t2 - t1 =2350-350=2000ч.
Принимая
= 2000 ч, находим среднюю наработку на
отказ
Интенсивность отказов
ср = 1/tср = 1/200 = 0,005 1/ч
Пример 2.3. Время работы изделия до отказа подчинено экспоненциальному закону распределения вероятностей отказов с параметром = 2,5 10-5 1/ч.
Определить характеристики P(t) , Tср при t = 500; 1000; 2000 ч.
Р е ш е н и е. Вероятность безотказной работы
P(t) = exp [-t] = exp [-2,5 10-5 t],
P(500) = exp [-2,5 10-5 500]= 0,9875,
P(1000) = exp [-2,5 10-5 1000]= 0,9753,
P(2000) = exp [-2,5 10-5 2000]= 0,9512.
Средняя наработка до первого отказа
Tср = 1/ = 1/2,5 10-5 = 40000 ч
При постоянной интенсивности отказов равнонадежных основных и резервных элементов при ненагруженном резервировании вероятность безотказной работы
где n –число последовательно соединенных элементов основной системы; S – время (наработка); m – число резервных элементов.
Пример 2.4. Определить вероятность безотказной работы машины, состоящей из четырех деталей, сгруппированных в три узла (рис.1).
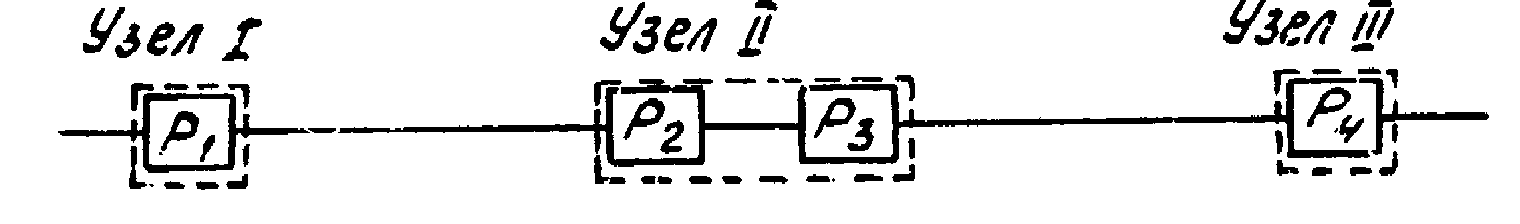
Рис.1
Вероятности безотказной работы деталей известны: P1=0,8; P2 = 0,9, P3 = 0,95; P4 = 0,98. Определим вероятность безотказной работы узлов:
PI = P1 = 0,8
PII = P2 P3 = 09 095 = 0,855,
PIII = P4 = 0,98
Вероятность безотказной работы машины
Pм = PI PII PIII = 0,8 0,855 0,98 = 0,67
Для повышения надежности резервируется деталь в узле I (рис.2), тогда
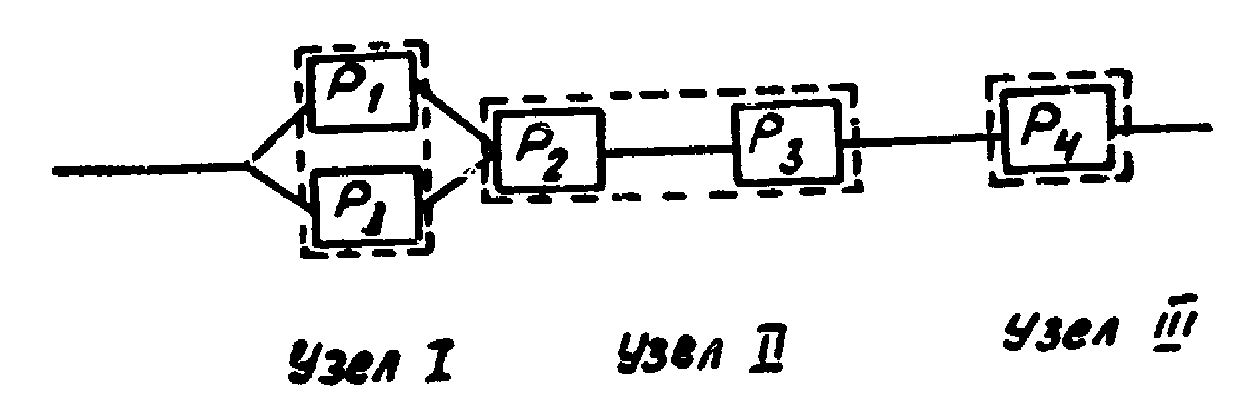
Рис.2
PI` = 1 - (1 - P1)2 = 1 - (1- 0,8)2 = 0,96
PII = P2 P3 = 0,855, PIII = P4 = 0,98
Pм = PI PII PIII = 0,96 0,855 0,98 = 0,81
т.е. безотказность возрастет более чем на 20 %.
Если резервировать также детали в узле II, то получим Pм=0,92, а при резервировании деталей в узле III получим Pм = 0,94. Данный расчет показывает, что наиболее эффективно резервирование наименее надежных деталей.
Задание на самостоятельную работу по расчету безотказности невосстанавливаемых систем при основном и резервном соединениях элементов
Задача 2.1. Определить вероятность безотказной работы вариантов системы из 4-х элементов ( P1 = 0,9; P2 = 0,8; P3 = 0,7; P4 = 0,6) .
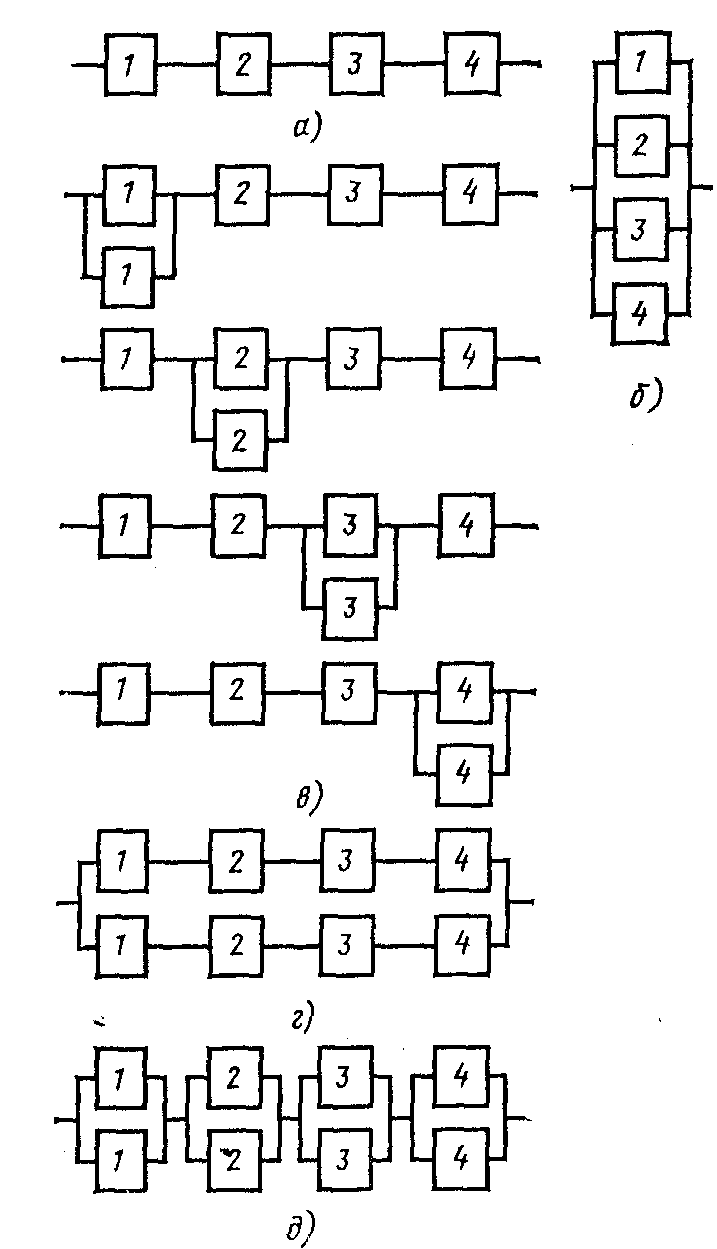
Задача 2.2. Определить требуемую вероятность безотказной работы трака
транспортной цепи ленточного экстрактора, если вероятность безотказной
работы экстрактора по транспортерной ленте за заданную наработку должна быть не менее 0,90. Число траков в ленте 40.
Задача 2.3. В результате анализа функционирования системы смазки оборудования, состоящей из последовательно соединенных (по основной схеме) насоса Н, фильтра Ф и радиатора Р выделено три возможных отказа: отказ вследствие чрезмерного давления масла после масляного насоса, отказ при работе системы с загрязненным фильтром,
отказ из-за падения давления при сливе жидкого масла через радиатор. Остальные элементы приняты абсолютно надежными. Решено для повышения безотказности дополнительно к насосу Н поставить редукционный клапан К1, дополнительно к фильтру Ф поставить перепускной клапан К2 и дополнительно к радиатору Р поставить предохранительный клапан К3. Варианты структурной схемы анализируемого участка представлены на рисунке.
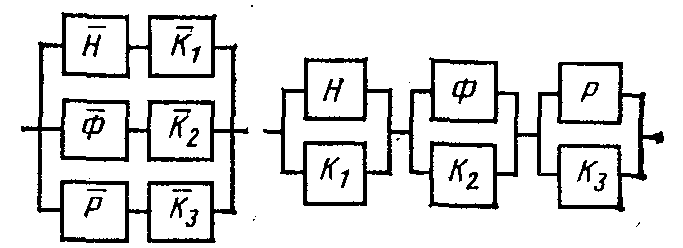
Определить вероятность безотказной работы выделенного участка системы смазки до введения и после введения в систему клапанов K1, K2, K3. Принять: вероятность отказа из-за чрезмерного давления масла после масляного насоса q1 = 0,2; вероятность отказа вследствие засорения фильтра q2 = 0,1; вероятность отказа вследствие угрожающего падения давления при сливе масла через радиатор q3 = 0,2; вероятность безотказной работы каждого клапана за требуемую наработку PK1 = РK2 = PK3 = 0,99. Вероятностями отказов по другим причинам можно пренебречь.
Задача 2.4. Для оборудования, имеющего четыре подшипника, интенсивность отказов подшипников = 1 10-6 1/ч. Определить вероятность выполнения наработки оборудования 6000 часов, если к четырем работающим подшипников имеется один запасной. Допускается в процессе работы замена только одного отказавшего подшипника.