Учет сферической земной поверхности

С феричность земли следует учитывать при r>0,2r₀. она проявляется в уменьшении разности хода прямой и отраженных волн. Для учета сферичности на разность хода вместо истинных высот h_A h_B вводят приведенные высоты h_A^' h_B^'.

Так как A,C,CB₁<<R_э можно считать

; .

с учетом Δ h_A Δh_B<<R_э

; ;

где .

При коротких пролетах (r≈0,2r₀)

.

При длинных пролетах

.

При этом

.

Для промежуточных случаев пользуются

.

Расходимость волны при отражении ее от сферической поверхности проявляется в увеличении угла отражения волны.

Для оценки соответствующего уменьшения модуля коэффициента отражения используются коэффициент расходимости, на который надо умножить коэффициент отражения. .

.

.

Коэффициент расходимости равен отношению площадей основания конуса для плоской и сферической поверхности.

Коэффициент отражения радиоволн и от земной поверхности определяется:

• степенью неровности отражающей поверхности;

• ее электрическими характеристиками;

• длинной волны;

• углом скольжения.

Если отражение от гладкой, плоской поверхности имеет зеркальный характер, то при этом модуль умножить коэффициента отражения равен примерно 1. Фазовый угол при малых углах скольжения Θ всегда можно считать равным 180⁰. Отражение от земной поверхности можно считать зеркальным, если высота неровностей удовлетворяет неравенству

– условие Рэлея.

– угол скольжения.

Если условие не выполняется, то рассеивание становится диффузионным.

Для решения вопроса в какой зоне вокруг точки отражения проверять выполнение условия Рэлея необходимо определить существенную зону отражающей поверхности.

Для этого используем принцип зеркального отражения. Для n зоны Френеля

;

.

В реальных условиях поэтому эллиптическая зона очень вытянута

Учет рельефа местности в условиях рефракции радиоволн

Н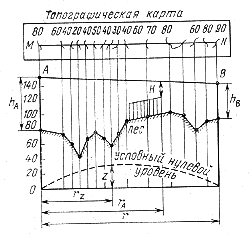 а пролетах реальных РРЛ имеются крупные неоднородности: холмы, впадины, овраги, жилые массивы. Так как значение характеристик рельефа имеют большой разброс, применяют приближенные детерминированные методы, учитывающие конкретные особенности пролетов РРЛ. Прежде всего строится продольный профиль пролета.

Для удобства профиль строят в прямоугольных координатах. При этом линия изображающая условный нулевой уровень (уровень моря) является параболой, для которой

.

.

Профиль строится путем нанесения высотных отметок снятых с топографической карты относительно нулевого уровня. При определении множителя ослабления принято пользоваться просветом Н между прямой соединяющей точки передачи А и прямой В и наивысшей точкой профиля пролета. В зависимости от значения просвета пролеты разделяются на открытые, полуоткрытые и закрытые.

Для открытых пролетов

где – (первая зона Френеля);

– относительная координата точки определяющей просвет на пролете.

То есть на отрытых пролетах эллипсоид, ограничивающий минимальная область РРВ не пересекается с земной поверхностью.

При полуоткрытых пролетах минимальная область распространения частично перерываются профилями пролета, однако, прямая видимость между точками расположения антенны сохраняется 0<H<H₀. Для закрытых пролетов H<0.

П риведенное выражение определяет нулевой уровень соответствующий случаю отсутствия рефракции. Для учета влияния рефракции вместо R используется R_э определяемое как

;

Из-за рефракции профиль пролета трансформируется. В условиях рефракции просвет равен

,

Н – просвет в отсутствии рефракции; ΔH(g) – изменение просвета из-за рефракции

.

В результате трансформации профилей, отрытые пролеты могут превратиться в полуоткрытые и даже закрытые, и наоборот.

РАСЧЕТ МНОЖИТЕЛЯ ОСЛАБЛЕНИЯ НА ОТКРЫТЫХ ПРОЛЕТАХ РРЛ

В точку приема В наряду с прямой волной попадает отраженная от земной поверхности. Для расчета множителя ослабления используется интерференционная формула. Для этого для конкретного пролета рассчитывается разность хода и коэффициент расходимости с учетом рефракции.

.

Для расчета используются приведенные высоты .

.

Рефракция незначительно влияет на , поэтому . Тогда

.

Относительный просвет

.

Максимумы и минимумы имеют место при

РАСЧЕТ МНОЖИТЕЛЯ ОСЛАБЛЕНИЯ НА ПОЛУОТКРЫТЫХ И ЗАКРЫТЫХ ПРОЛЕТАХ

На полуоткрытых закрытых пролетах радиоволны распространяются благодаря дифракции. Согласно принципа Гюйгенса дифракция радиоволн возникает в результате попадания в точку приема вторичных волн, излучаемых не закрытой препятствиями частью фронта волны, то есть видимой частью зон Френеля.

Р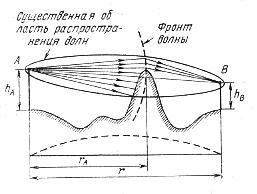 ассмотрим закрытый (или полуоткрытый) пролет (H<H₀) с одним препятствием. В этом случае приближенно множитель ослабления дБ

,

где V_кас – значение модуля множителя ослабления, соответствующий касательному пролету (H=0), дБ

,

нормированный просвет, Н₀-соответствует первой зоне Френеля.

Величина V_кас зависит от степени клиновидности препятствия, которая характеризуется параметром, μ изображена на рисунке.

При аппроксимации препятствия сферой с высотой сегмента Δy и длинной хорды r_в параметр μ

,

где:

; .

На полуоткрытых и слабо закрытых пролетах r_в определяется как расстояние между точками пересечения прямой параллельной АВ и отстоящей от вершины препятствия на Δy=H₀ .

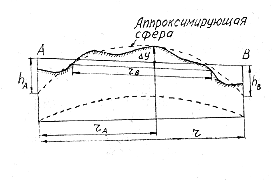
На закрытых пролетах r_в определяется как расстояние между точками касания касательных проведенных из точек А и В к профилю пролета. Величина Δy выбирается при этом равным расстоянию между вершиной препятствия и хордой.

Поведение зависимости множителя ослабления от значений нормированного просвета p(g) представлено на рисунке.

П ри фиксированном значении p(g) в области тем больше, чем больше . При форма препятствия приближается к клиновидной. Значение соответствует плоским трассам у которых при (опущенные на поверхность земли точки прием и передачи). Возрастание по мере увеличения объясняет явление под названием “выигрыш за счет препятствия”.