1Лабораторная работа № 1

СТАТИСТИЧЕСКИЙ АНАЛИЗ ПРОИЗВОДСТВЕННЫХ ОБЪЕКТОВ

Цель занятия

1 Изучить методы математической статистики, используемые для получения основных характеристик производственных объектов

2 Изучить методы проверки статистических гипотез

3 Выполнить расчеты по заданию, выданному преподавателем, и проанализировать полученные результаты

Порядок выполнения работы

1 Изучить основные статистические характеристики производственных объектов

2 Изучить методы проверки статистических гипотез

3 Получить исходные данные у преподавателя

4 Выполнить расчеты

5 Оформить отчет с результатами расчетов и проанализировать полученные данные

Содержание отчета

1 Ответы на контрольные вопросы

2 Исходные данные

3 Результаты расчетов с анализом полученных данных

4 Выводы

Контрольные вопросы

1 Основные статистические характеристики производственных объектов

2 Нормальное распределение

3 Проверка статистической гипотезы о законе распределения (критерий Пирсона)

1.1Вариационные ряды и их характеристики

При решении многих прикладных задач, в частности, для составления моделей и алгоритмов управления объектами автоматизации, необходимы вероятностные характеристики случайных факторов, присущих объекту исследования. В большинстве случаев эти характеристики неизвестны исследователю и определяются по экспериментальным данным.

Кратко охарактеризуем методы, используемые при статистическом анализе случайных величин.

Установление статистических закономерностей, присущих массовым случайным явлениям, основано на изучении статисти­ческих данных — сведений о том, какие значения принял в ре­зультате наблюдений интересующий нас признак (случайная ве­личина X).

В практике статистических наблюдении различают два вида наблюдений: сплошное, когда изучаются все объекты (элементы, единицы) совокупности, и выборочное, когда изучается часть объектов. Теоретическую основу применимости выборочного метода составляет закон больших чисел, согласно которому при неогра­ниченном увеличении объема выборки практически достоверно, что случайные выборочные характеристики как угодно близко приближаются (сходятся по вероятности) к определенным пара­метрам генеральной совокупности.

Различные значения признака (случайной величины X) называются вариантами (обозначим их через x).

П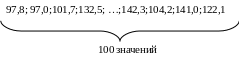 ример. Получены следующие данные о распределении 100 рабочих цеха по выработке в отчетном году (в процентах к предыдущему году):

Первый шаг к осмыслению имеющегося статистического ма­териала — это его упорядочение, расположение вариантов в по­рядке возрастания (убывания), т.е. ранжирование вариантов ряда:

x_min … x_max

В таком виде изучать выборку тоже не очень удобно из-за обилия числовых данных. Поэтому разобьем вари­анты на отдельные интервалы, т.е. проведем их группировку. Число интервалов т следует брать не очень большим, чтобы после группировки ряд не был громоздким, и не очень малым, чтобы не потерять особенности распределения признака.

Согласно формуле Стерджеса рекомендуемое число интерва­лов т = 1 + 3,3221gn, a величина интервала (интервальная раз­ность, ширина интервала):

где x_max – x_min — разность между наибольшим и наименьшим значениями признака.

Сгруппированный ряд представляют в виде таблицы (табл.1.1).

Таблица 1.1

i	Интервал [xi, xi+1]	Частота ni	Частость wi=ni/n	Накопленная частота niнак	Накопленная частость wi нак= niнак/n
1	94,0-100,0	3	0,03	3	0,03
2	100,0-106,0	7	0,07	10	0,1
3	106,0-112,0	11	0,11	21	0,21
4	112,0-118,0	20	0,2	41	0,41
5	118,0-124,0	28	0,28	69	0,69
6	124,0-130,0	19	0,19	88	0,88
7	130,0-136,0	10	0,1	98	0,98
8	136,0-142,0	2	0,02	100	1
		100	1,00	—	—

Числа, показывающие, сколько раз встречаются варианты из данного интервала, называются частотами (обозначаем n_i), а отношение их к общему числу наблюдений – частостями или относительными частотами, т.е. w_i=n_i/n. Частоты и частости называются весами.

Определение. Вариационным рядом называется ран­жированный в порядке возрастания или убывания ряд вариантов с соответствующими им весами (частотами или частостями)

При изучении вариационных рядов наряду с понятием час­тоты используется понятие накопленной частоты (обозначаем n_i^нак). Накопленная частота показывает, сколько наблюдалось вариантов со значением признака, меньшим х. Отношение на­копленной частоты n_i^нак к общему числу наблюдений я назовем накопленной частостью w_i^нак= n_i^нак/n.

Накопленные частоты (частости) для каждого интервала нахо­дятся последовательным суммированием частот (частостей) всех предшествующих интервалов, включая данный. Для задания вариационного ряда достаточно указать вариан­ты и соответствующие им частоты (частости) или накопленные частоты (частости) (в табл. 1.1 приведены и те, и другие).

Вариационный ряд называется дискретным, если любые его варианты отличаются на постоянную величину, и – непрерыв­ным (интервальным), если варианты могут отличаться один от другого на сколь угодно малую величину.

Для графического изображения вариационных рядов наиболее часто используются полигон, гистограмма, кумулятивная кривая.

Полигон, как правило, служит для изображения дискретного вариационного ряда и представляет собой ломаную, в которой концы отрезков прямой имеют координаты (x_i, n_i), i =1,2,..., m.

Гистограмма служит только для изображения интервальных вариационных рядов и представляет собой ступенчатую фигуру из прямоугольников с основаниями, равными интервалам зна­чений признака k_i = x_i-1 – x_i; i =1,2,...,т, и высотами, равными частотам (частостям) n_i (w_i) интервалов. Если соединить середи­ны верхних оснований прямоугольников отрезками прямой, то можно получить полигон того же распределения.

Кумулятивная кривая (кумулята) — кривая накопленных час­тот (частостей). Для дискретного ряда кумулята представляет ломаную, соединяющую точки (x_i, n_i^нак) или (x_i, w_i^нак), i = 1,2,..., т.

Для интервального вариационного ряда ломаная начинается с точки, абсцисса которой равна началу первого интервала, а ор­дината — накопленной частоте (частости), равной нулю. Другие точки этой ломаной соответствуют концам интервалов.

Весьма важным является понятие эмпирической функции распределения.

Определение. Эмпирической функцией распределения F_n(x) называется относительная частота (частость) того, что признак (случайная величина X) примет значение, меньшее заданного х, т. е.

F_n(x)=w(X<x) = w_x^нак (1.1)

Другими словами, для данного х эмпирическая функция рас­пределения представляет накопленную частость w_x^нак = n_x^нак / n.

Вариационный ряд является статистическим аналогом (реализацией) распределения признака (случайной величины X). В этом смысле полигон (гистограмма) аналогичен кривой распре­деления, а эмпирическая функция распределения — функции распределения случайной величины X.

На практике часто оказывается достаточным знание лишь сводных характеристик вариационных рядов: средних или характеристик центральной тенденции; ха­рактеристик изменчивости (вариации) и др. Расчет статистических характеристик представляет собой второй после группиров­ки этап обработки данных наблюдений.