Варіанти завдань
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
Задача 2
Встановити
тип кривої другого порядку
та знайти :
для кола – координати центра та радіус;
для еліпса – координати центра, півосі, ексцентриситет;
для гіперболи – координати центра, дійсну та уявну півосі, координати фокусів, ексцентриситет, рівняння асимптот;
для параболи – параметр параболи, координати вершини, координати фокуса, рівняння директриси.
Схематично зобразити криві.
[7, с. 14-18; 11, с. 32-34].
Варіанти завдань
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
Завдання 5 Аналітична геометрія у просторі
Задано
координати вершин піраміди
Знайти :
1)
рівняння прямої L,
яка проходить через точки
і
,
та довжину ребра
;
2)
рівняння площини Р, яка проходить через
точки
;
3)
рівняння висоти Н, опущеної з вершини
на грань
та її довжину;
4) об'єм V піраміди;
5)
кут α між ребрами
та
;
6) кут β між ребром та гранню .
[7, с. 18-21; 11, с. 37-41].
Зробити рисунок.
Варіанти завдань
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
Контрольна робота 2
Завдання 1 Границі функції
Обчислити границі заданих функцій.
[8, с. 5-11; 10, с. 21-23].
Варіанти завдань
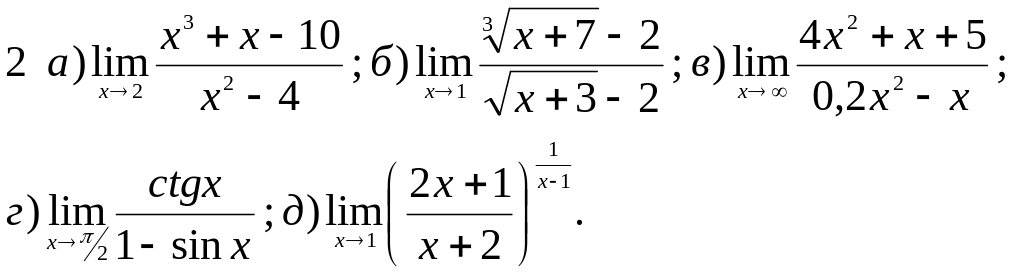
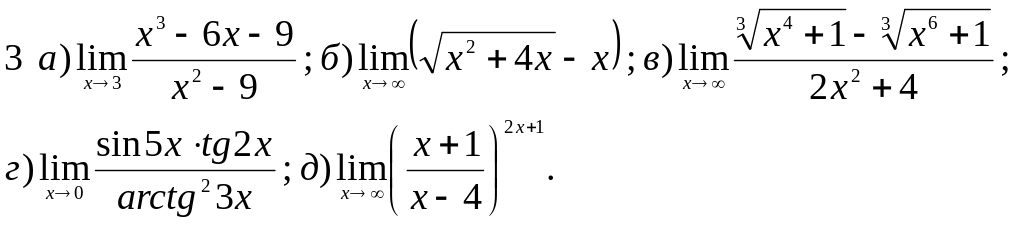
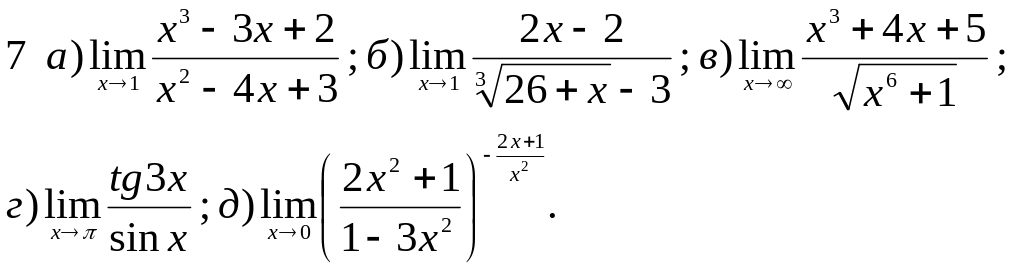
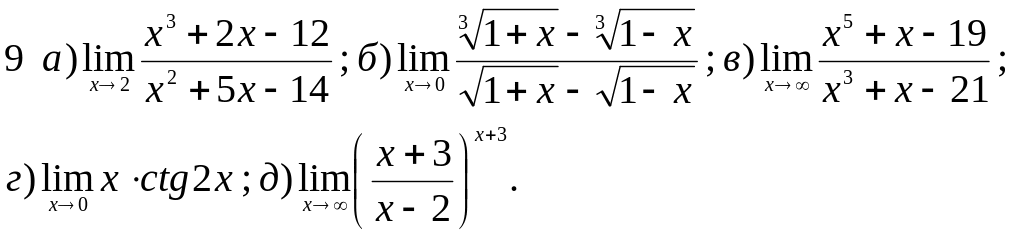
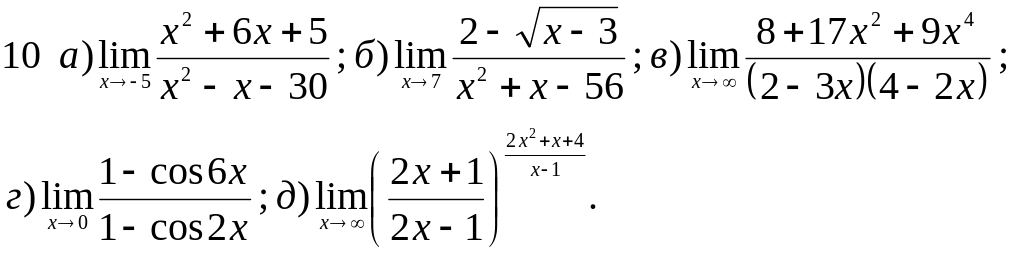
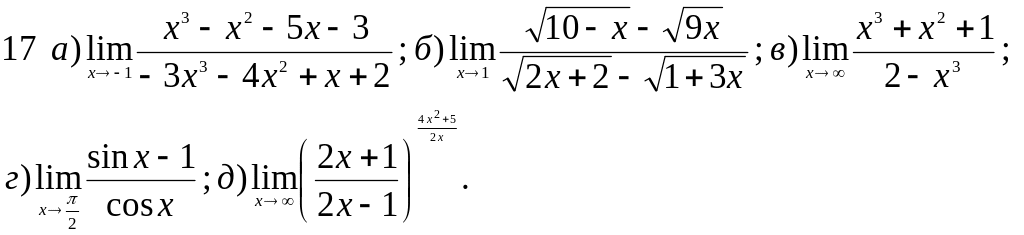
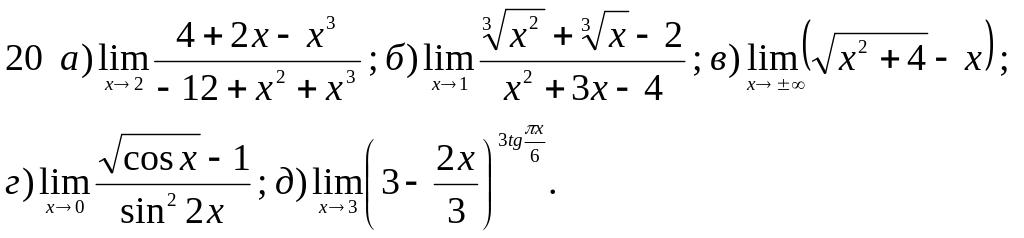
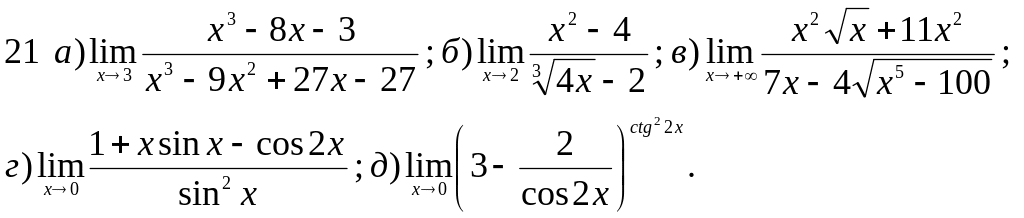
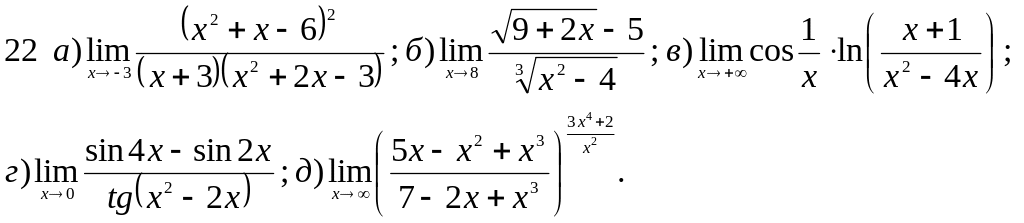
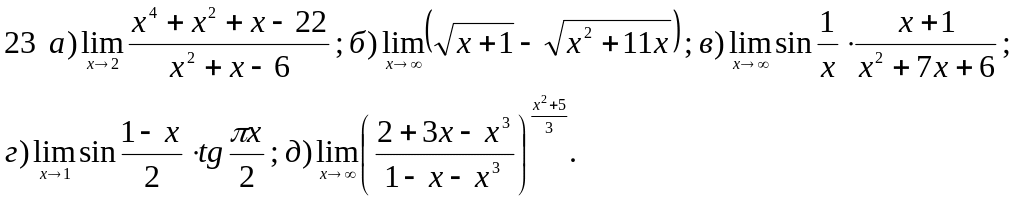
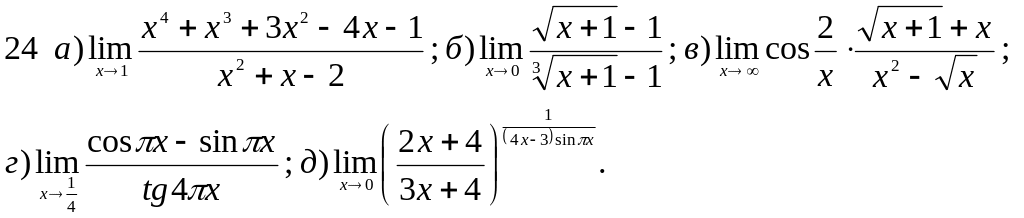
Завдання 2 Диференціальне числення функцій однієї змінної
Задача 1
Продиференціювати задані функції.
У
пунктах “а” – “д” знайти похідну
;
у
пункті “е” знайти першу і другу похідні
,
диференціал функції
;
у
пункті “ж” знайти
.
(див.
,
с.12-19,
,
с.23-26.)
Варіанти завдань
1
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
г)
.
2
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
г)
.
3
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
;
г)
.
4
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
;
г)
.
5
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
.
г)
.
6
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
.
г)
.
7
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
.
г)
.
8
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
.
г)
.
9
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
.
г)
.
10
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
.
г)
.
11
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
.
г)
.
12
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
.
г)
.
13
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
;
г)
.
14
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
;
г)
.
15
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
;
г)
.
16
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
;
г)
.
17
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
;
г)
.
18
а)
;
д)
;
б)
;
е)
;
в)
у=
;
ж)
;
г)
.
19
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
;
г)
.
20
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
;
г)
.
21
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
;
г)
.
22
а)
;
д)
;
б)
;
е) у=
;
в)
;
ж)
;
г)
.
23
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
;
г)
.
24
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
;
г)
.
25
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
г)
.
26
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
г)
.
27
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
;
г)
.
28
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
;
г)
.
29
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
;
г)
.
30
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
;
г)
.
31
а)
;
д)
;
б)
;
е)
;
в)
;
ж)
;
г)
.
Задача 2
Знайти границі, використовуючи правило Лопіталя:
а)
б)
в)
г)
д)
Розкриття
невизначеностей типу
та
за допомогою правила Лопіталя..
Теорема(
правило
Лопіталя).
Якщо функції
та
:
неперервні, диференційовані та
в
деякому околі точки
;прямують до нуля (або
)
при
;існує границя
(скінчена або нескінченна, рівна
або
),
то
існує і
,причому
Правило
Лопіталя справедливе і при
Правило Лопіталя може застосовуватись
повторно. На кожному етапі застосування
слід користуватись спрощуючими тотожними
перетвореннями, а також комбінувати це
правило з будь-якими іншими способами
обчислення границь.
Розкриття
невизначеностей типу
та
.
У цих випадках слід алгебраїчно перетворити дану функцію так, щоб привести її до визначеностей типу або , а далі використовувати правило Лопіталя:
а)
нехай
при
Перетворимо
таким чином:
або
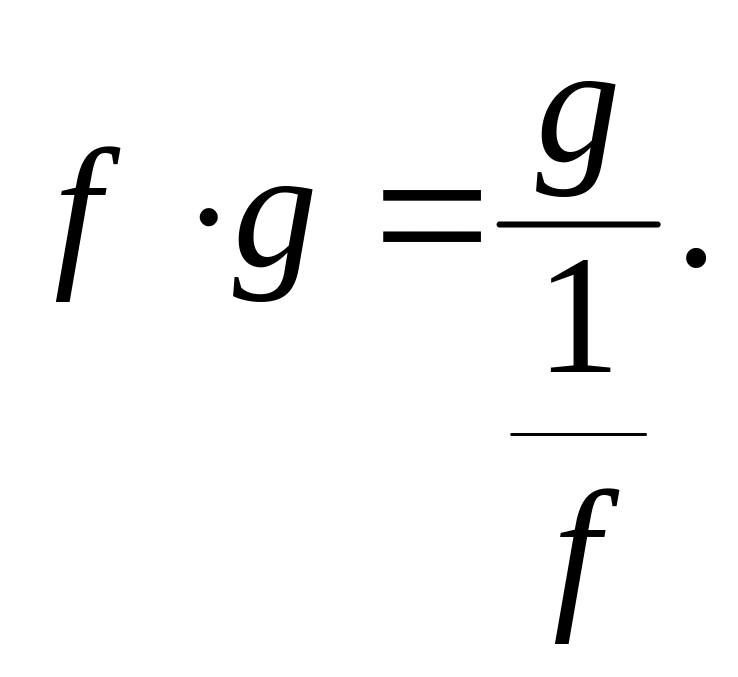Тоді
маємо невизначеність типу
або
при
;
б)
нехай
при
Перетворимо вираз
таким чином:
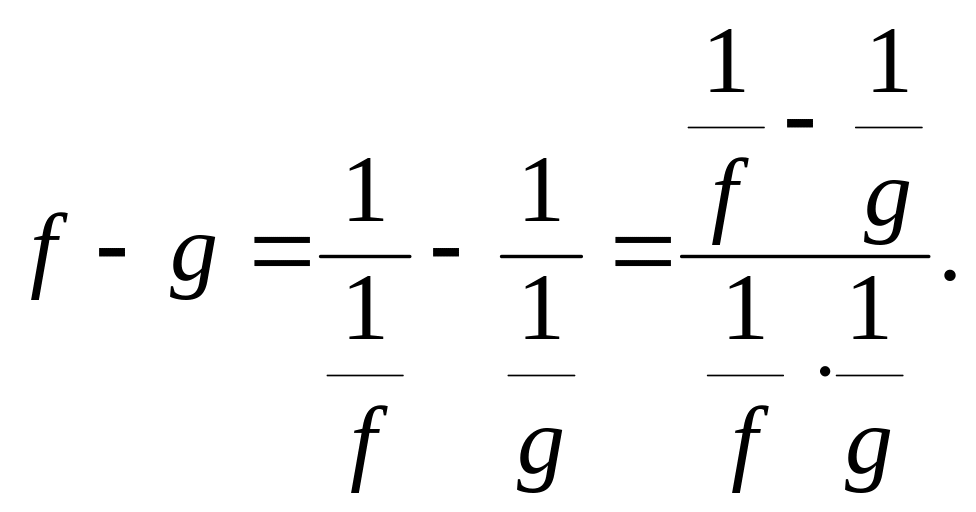Маємо невизначеність типу
при
Розкриття
невизначеностей типу
У
всіх трьох випадках розглядаємо границі
виразу
при
,
причому:
якщо
маємо невизначеність типу
якщо
маємо невизначеність типу
якщо
маємо невизначеність типу
Перетворимо
вираз
таким чином:
У
всіх трьох випадках вираз
при
представляє невизначеність типу
До такого ж результату приходимо, якщо
попередньо прологарифмуємо ліву та
праву частини рівності:
або
Отже, розв’яжемо приклади. Знайти границі, використовуючи правило Лопіталя:
а)
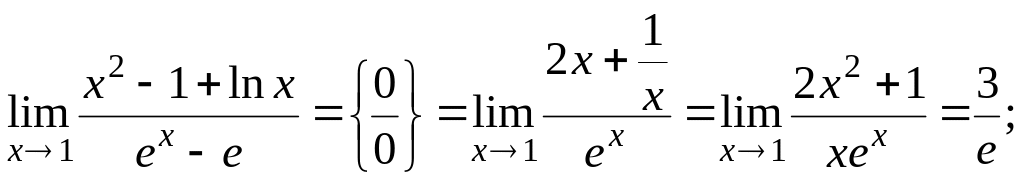
б)
=
в)
=
г)
=
=
д)
Знайдемо
границю
за правилом Лопіталя:
Отже,
