
Зміст
Конрольна робота 1
Завдання 1 Дії над матрицями………………………………………3
Завдання 2 Системи лінійних рівнянь……………………………...7
Завдання 3 Векторна алгебра……………………………………...11
Завдання 4 Аналітична геометрія на площині……………………16
Завдання 5 Аналітична геометрія у просторі…………………….19
Контрольна робота 2
Завдання 1 Границі функції………………………………………..20
Завдання 2 Диференціальне числення функцій однієї змінної….26
Завдання 3 Теорія функцій кількох змінних……………………...41
Список літератури………………………………………………….48
Контрольна робота 1
Завдання 1 Дії над матрицями
Знайти матрицю С, виконавши вказані операції над матрицями А та В [7, с.4-5; 9, с.6-7, 19-20].
Варіанти завдань
1
С=2(А+В);
![]() ,
,
![]()
2
С=А(2А+В);
 ,
,
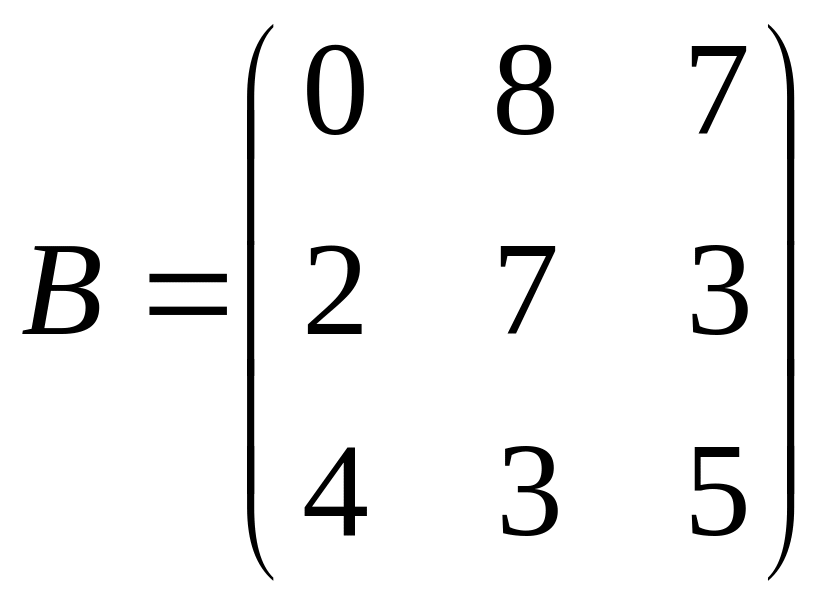 .
.
3
С=2А(А+В);
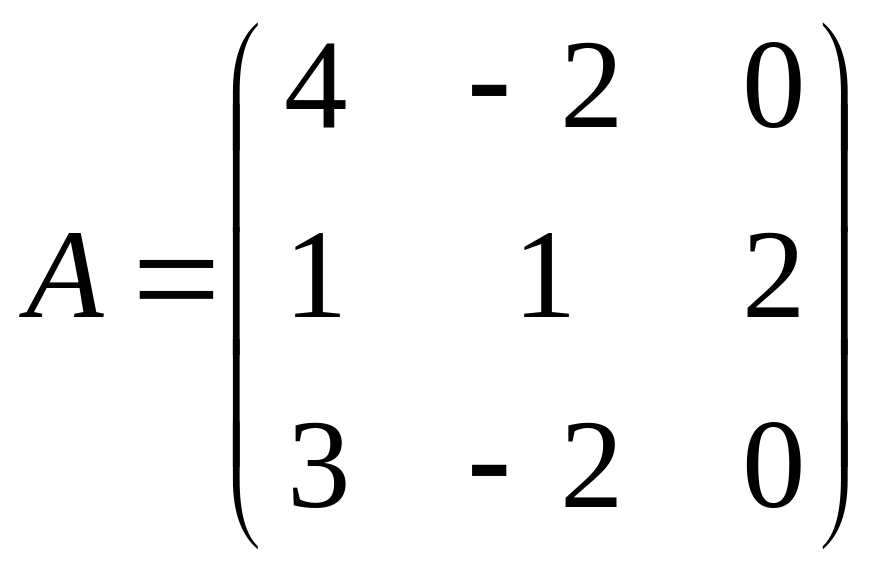 ,
,
 .
.
4
С=3В(В-2А);
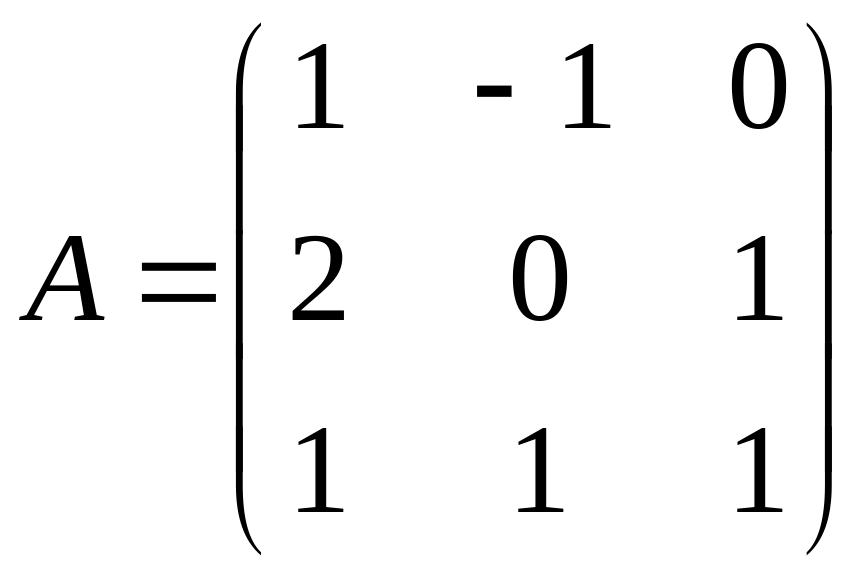 ,
,
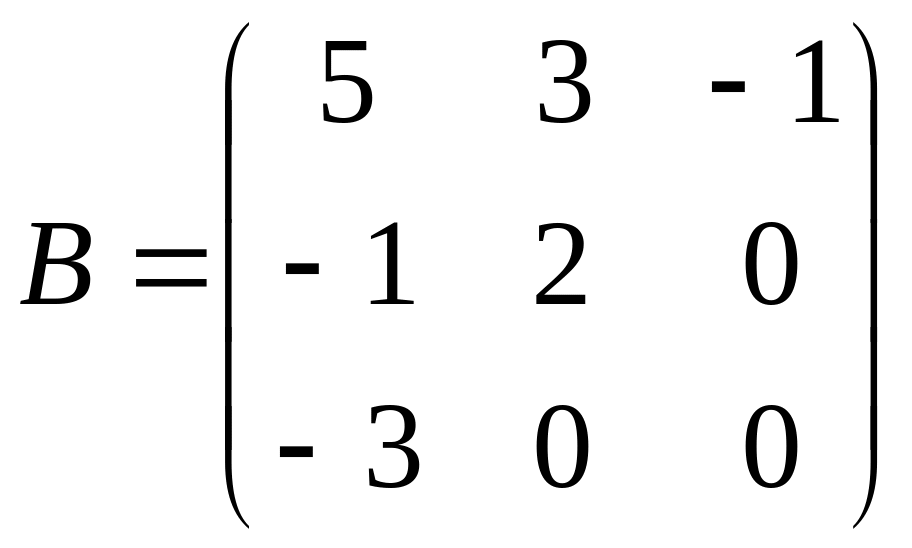 .
.
5
С=2В(В-А);
 ,
,
 .
.
6
С=2А(А-В);
 ,
,
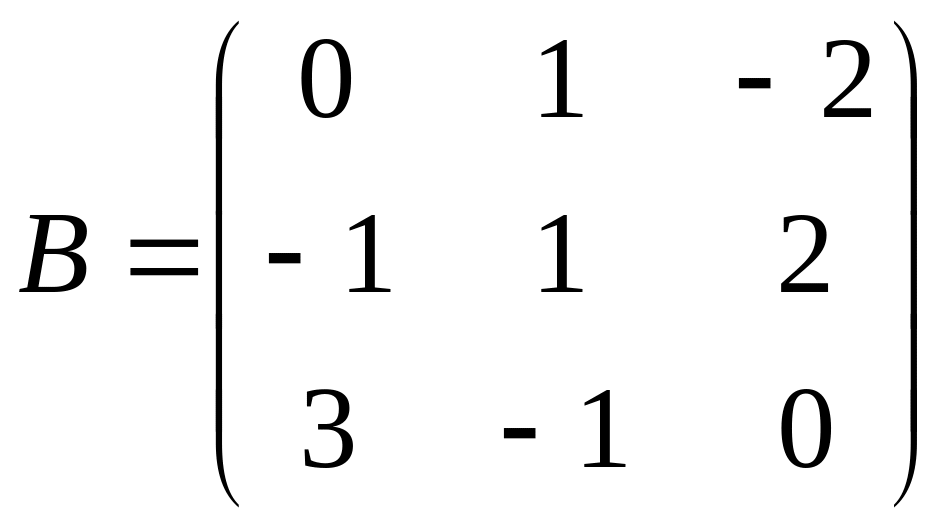 .
.
7
С=В(А-3В);
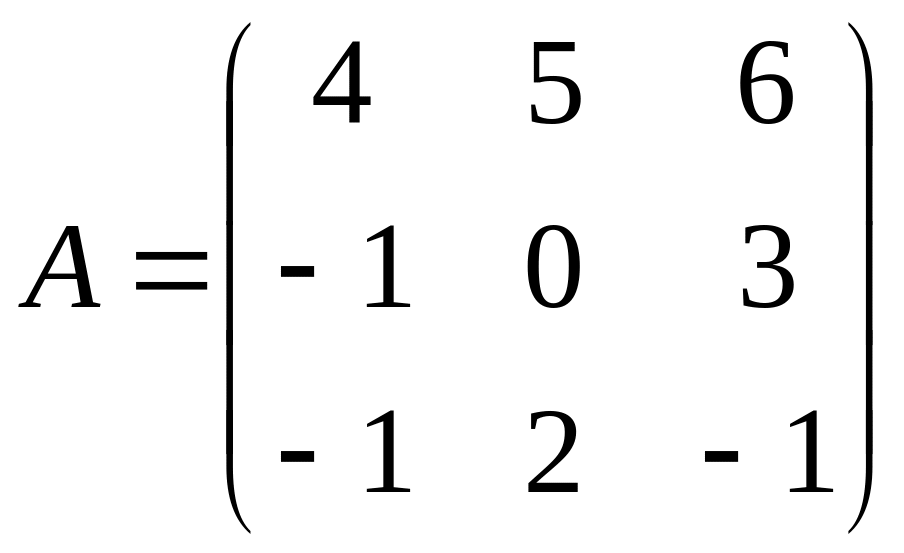 ,
,
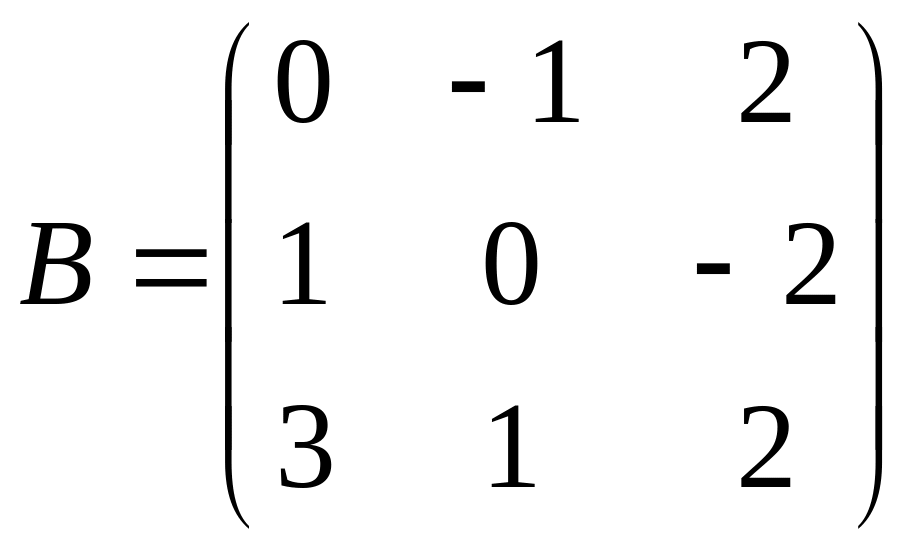 .
.
8
С=В(А+2В);
 ,
,
 .
.
9
С=2А(2В-А);
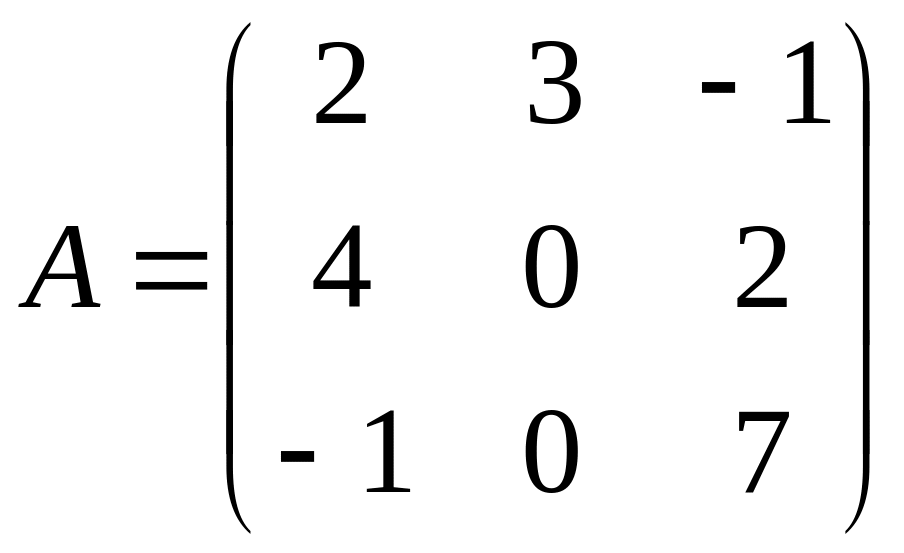 ,
,
 .
.
10
С=(А+2В);
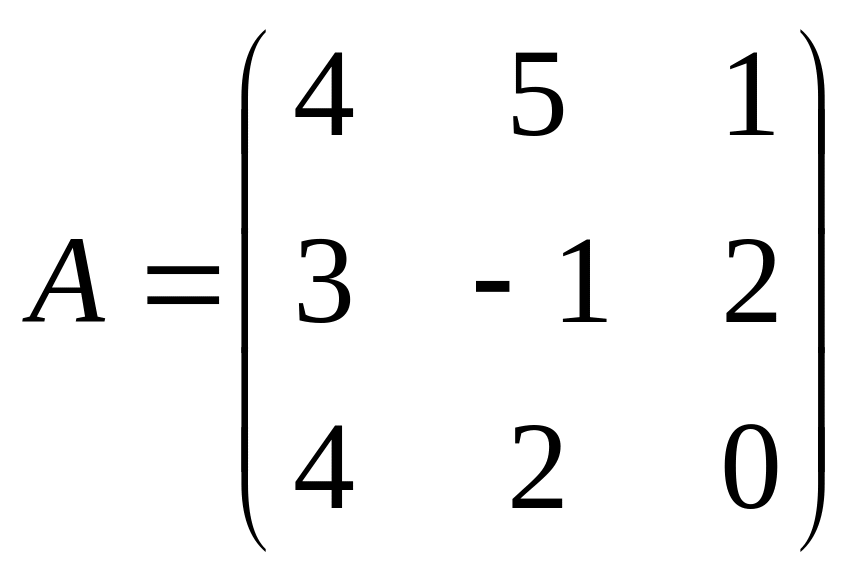 ,
,
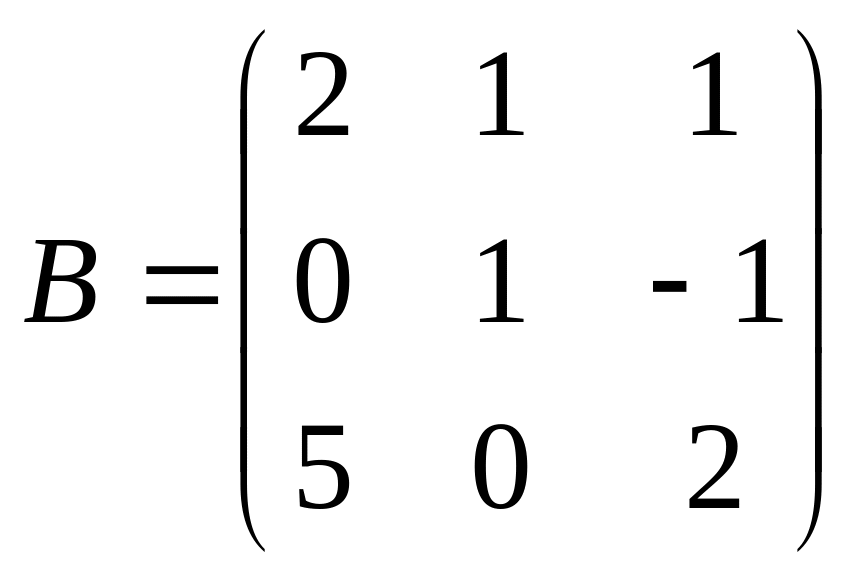 .
.
11
С=2(А-В);
![]() ,
,
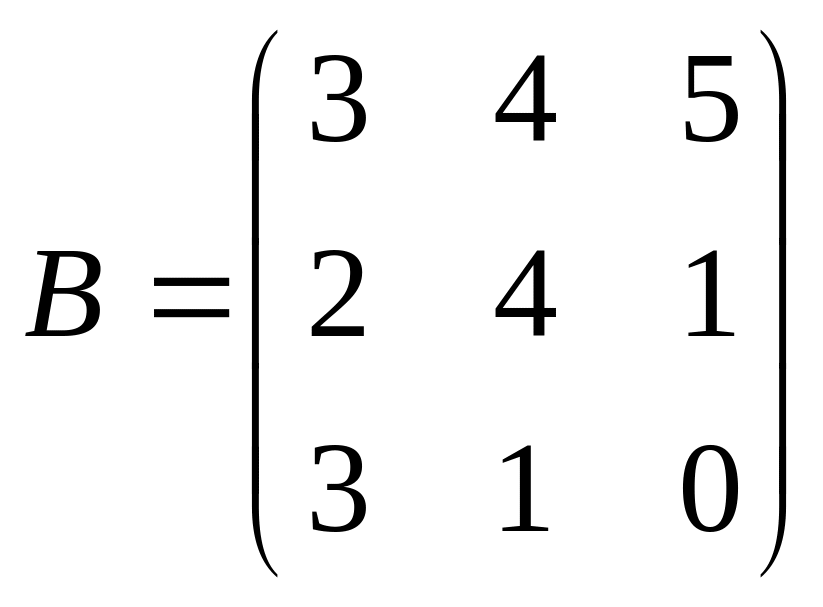 .
.
12
С=В(А-3В);
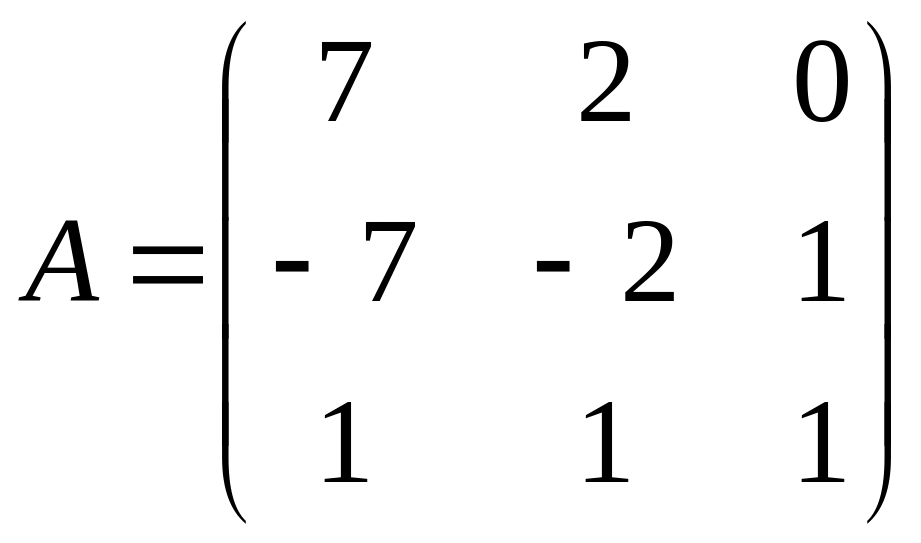 ,
,
 .
.
13
С=А(2А+B);
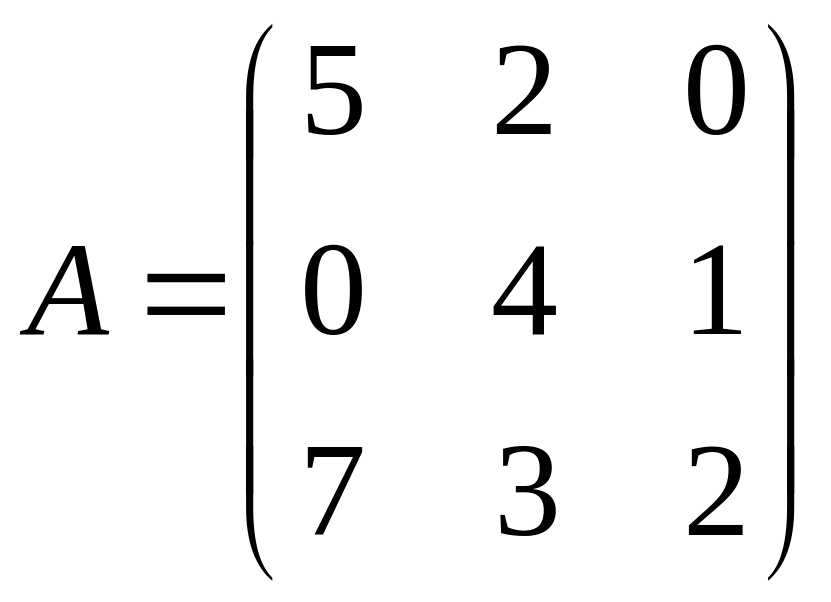 ,
,
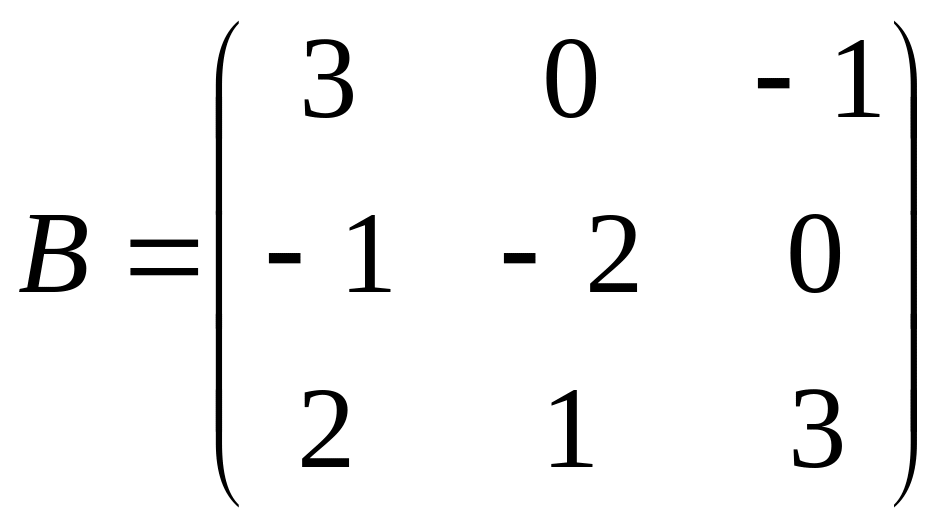 .
.
14
С=(А-В)2А;
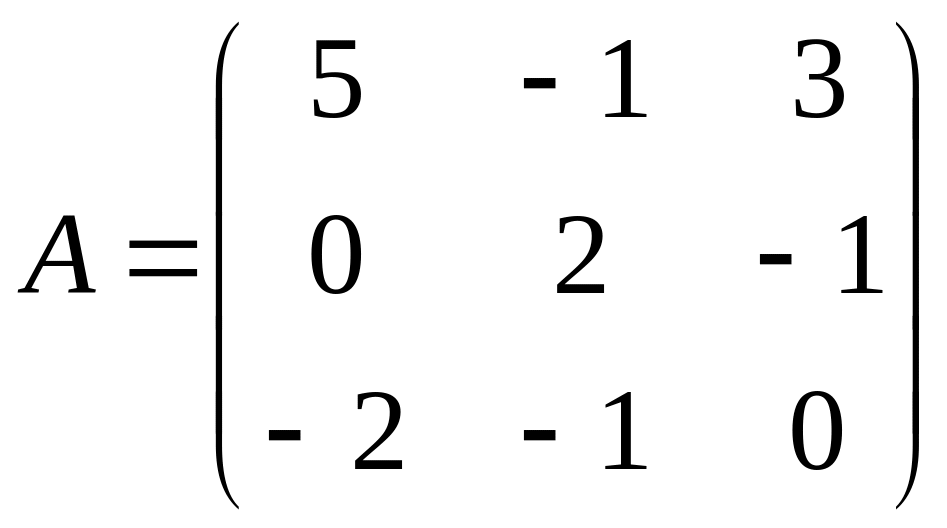 ,
,
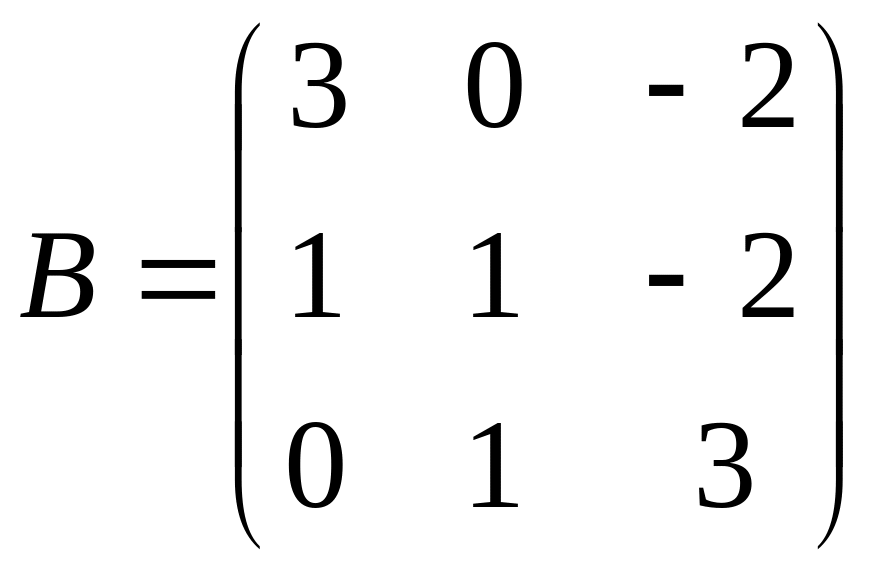 .
.
15
С=(А-2В)В;
 ,
,
 .
.
16
С=2(А-В)А;
 ,
,
 .
.
17
С=2А(А+В);
 ,
,
 .
.
18
С=3(А-В)В;
 ,
,
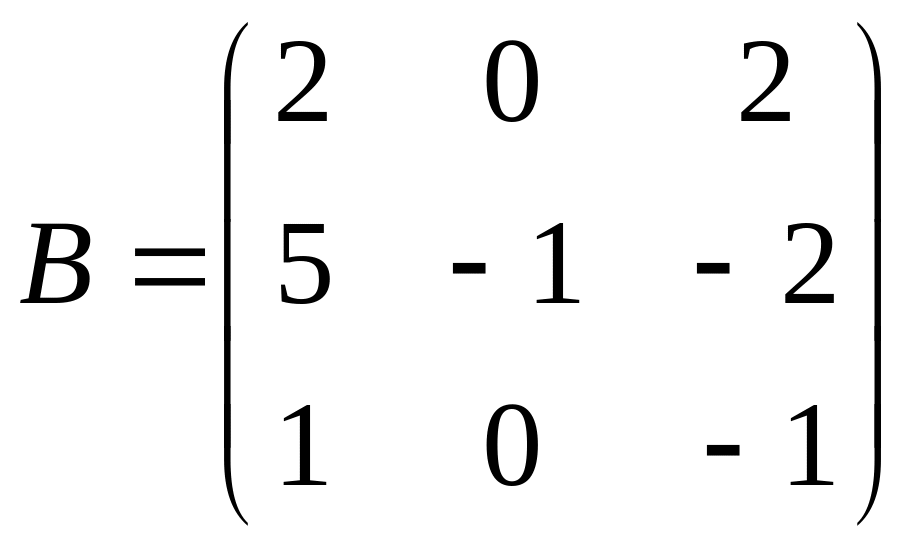 .
.
19
С=(2А-В)А;
 ,
,
 .
.
20 С=В(А+2В); , .
21
С=2(В-А)А;
 ,
,
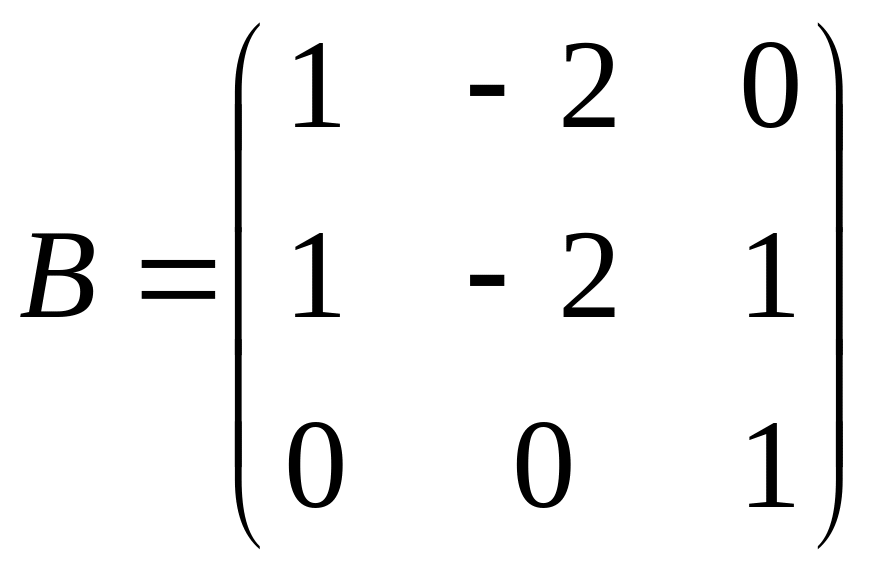 .
.
22
С=3(А+В)В;
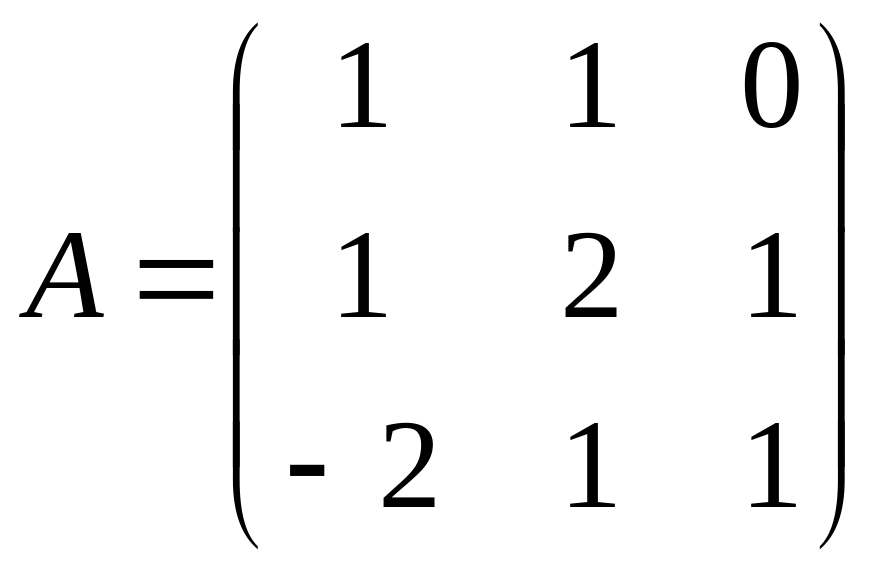 ,
,
 .
.
23
С=2А(А+В);
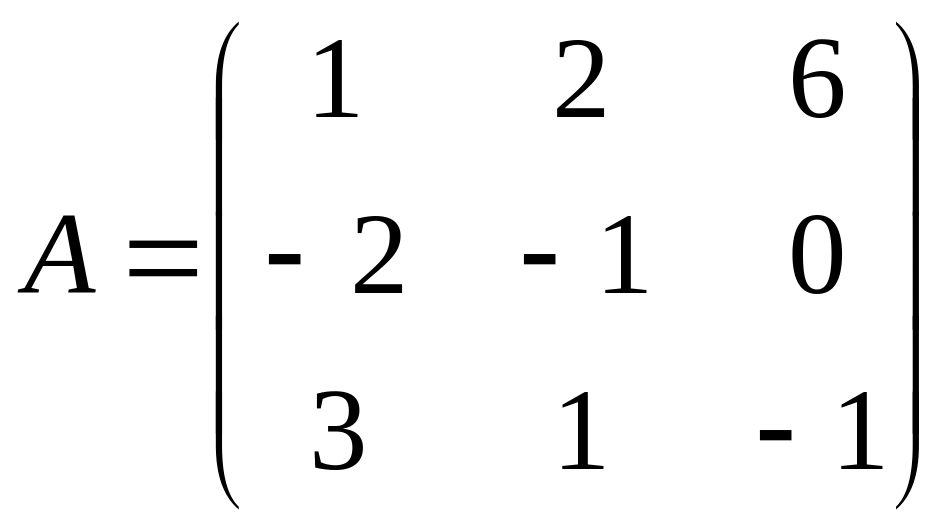 ,
,
 .
.
24
С=В(2В-3А);
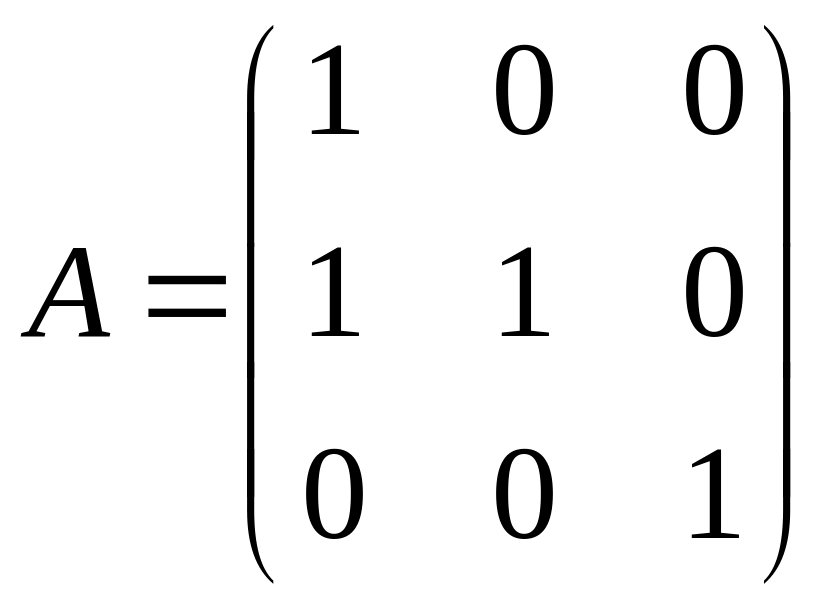 ,
,
 .
.
25
С=2А(В+А);
 ,
,
 .
.
26
С=В(2А-В);
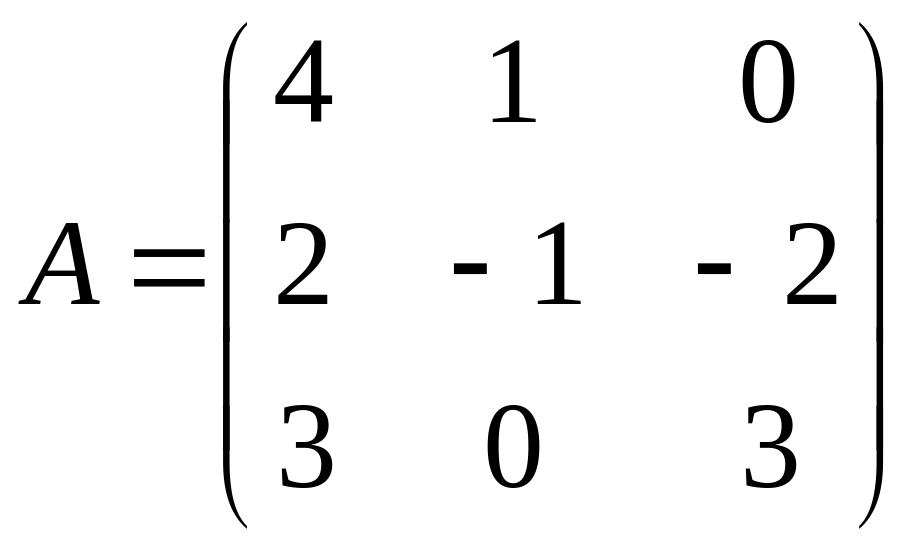 ,
,
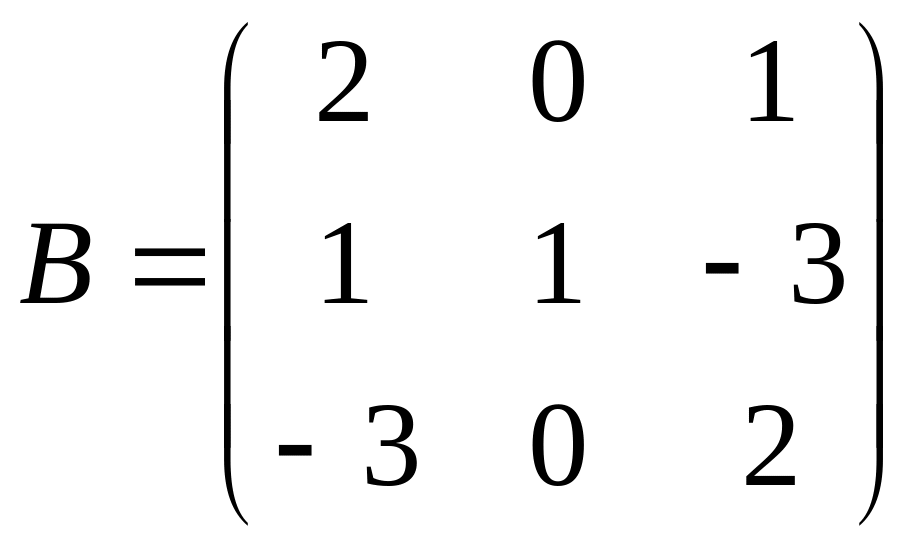 .
.
27
С=(3А-2В)В;
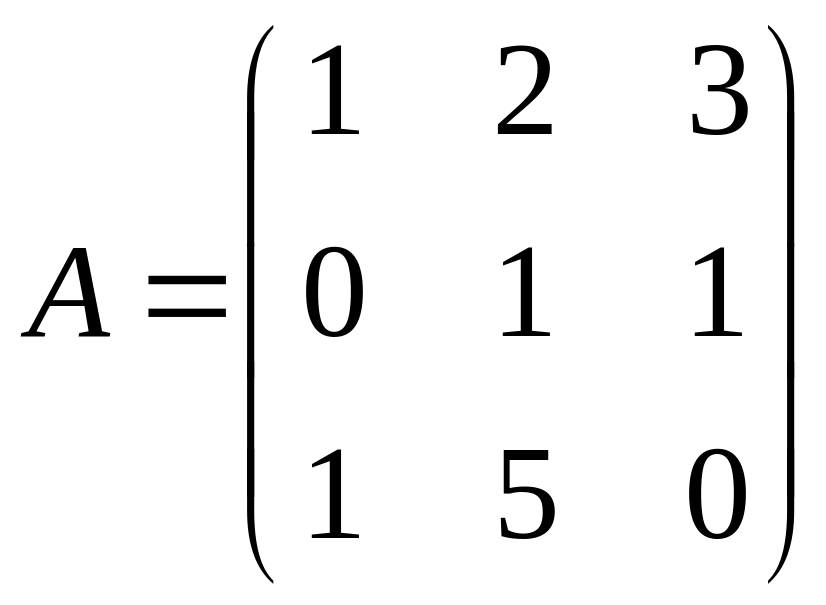 ,
,
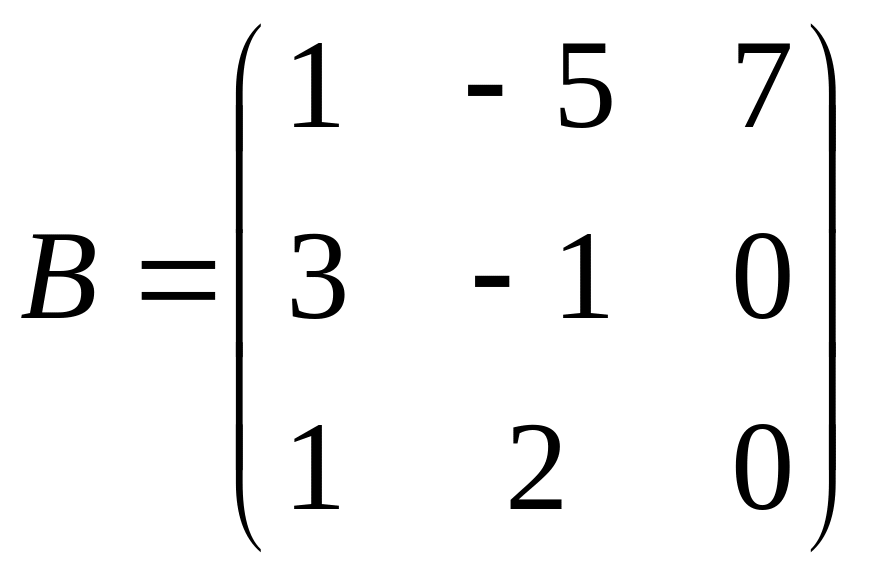 .
.
28
С=(А-2В)А;
 ,
,
 .
.
29
С=(А+2В)А;
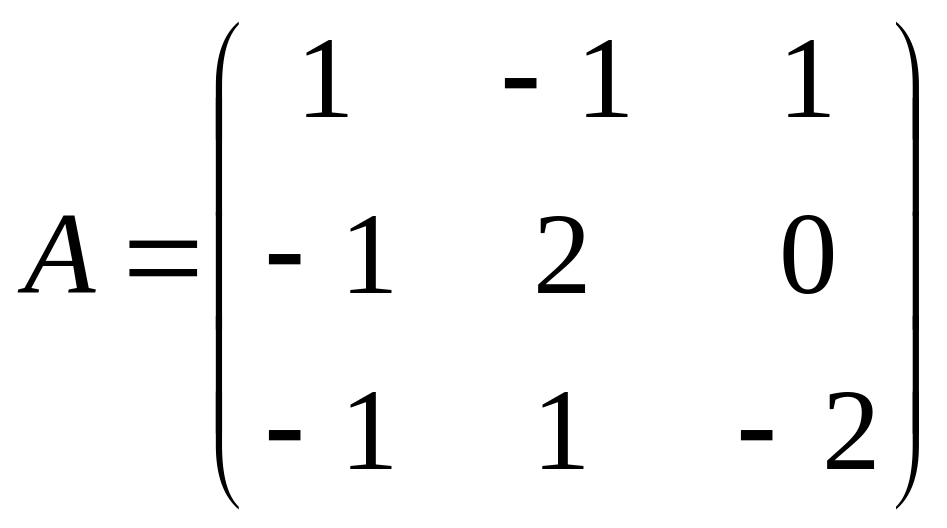 ,
,
 .
.
30
С=(А-2В)В;
 ,
,
 .
.
31
С=(А+3В)2В;
 ,
,
 .
.
Завдання 2 Системи лінійних рівнянь
а) розв'язати задану систему лінійних рівнянь трьома методами:
1) за формулами Крамера. Виконати перевірку; 2) матричним методом; 3) методом Гауса [7, с. 7-13; 9, с. 4-6, 23-24].
Варіанти завдань
1
 2
2
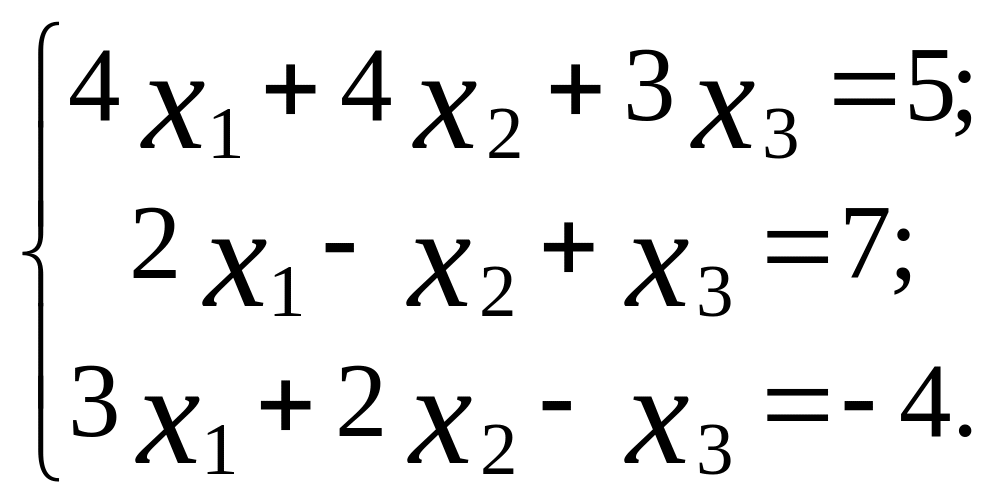
3
 4
4
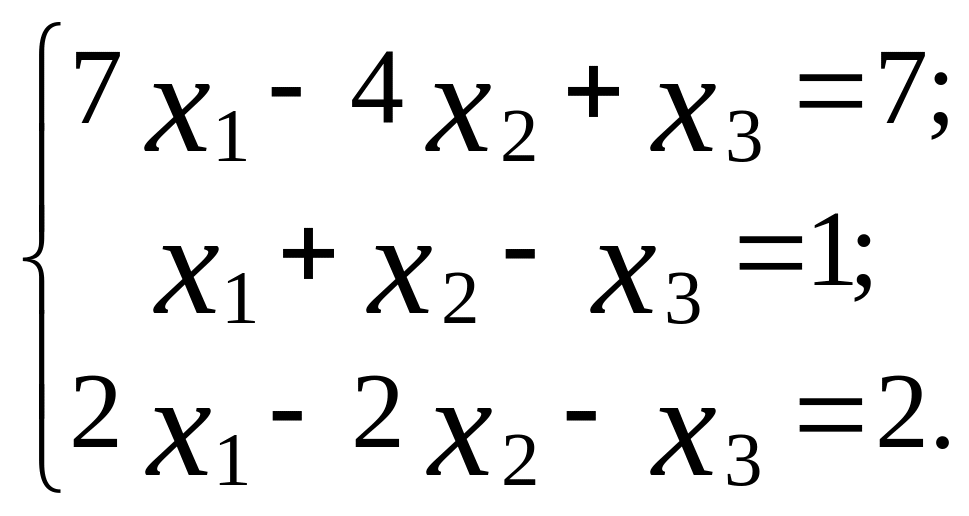
5
 6
6

7
 8
8
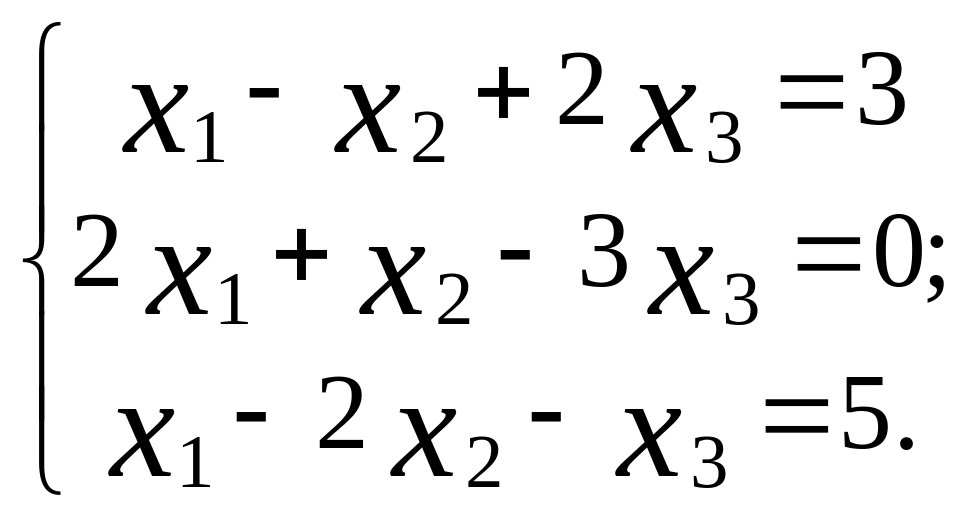
9
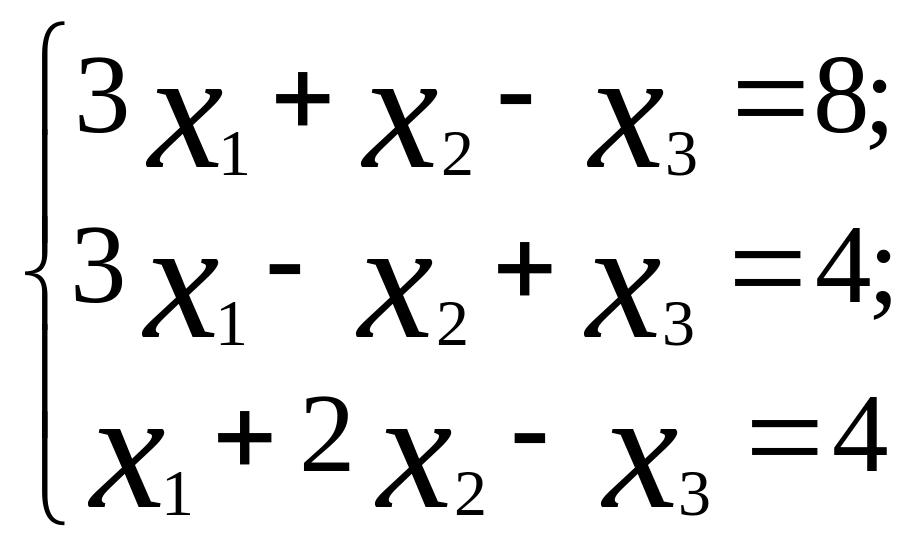 10
10

11
 12
12
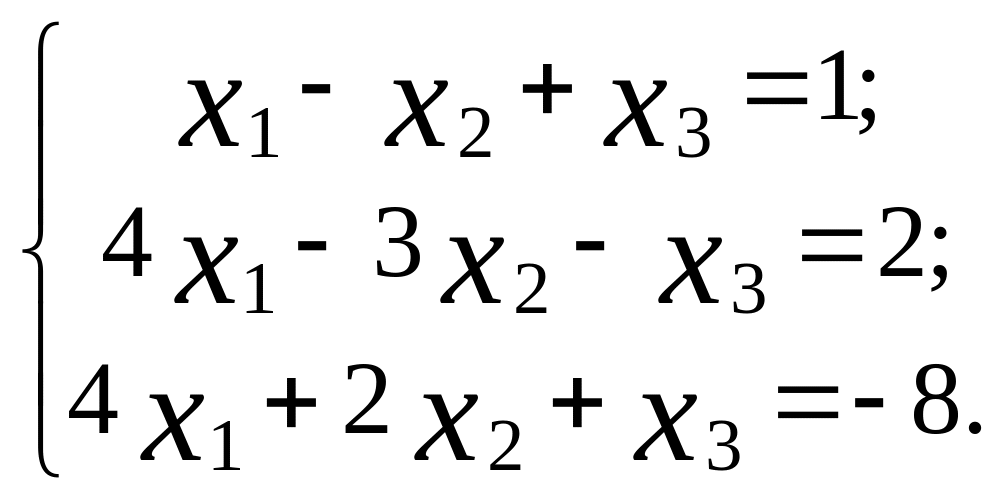
13
 14
14
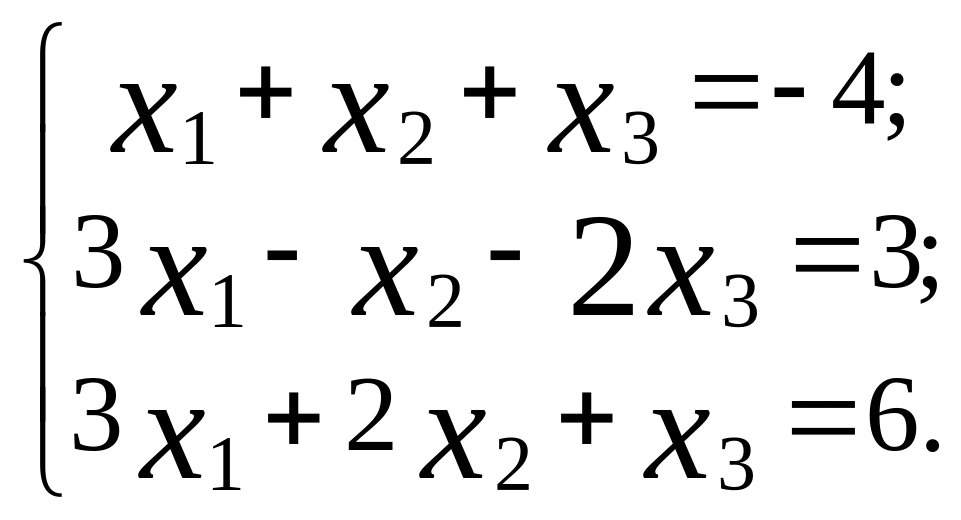
15
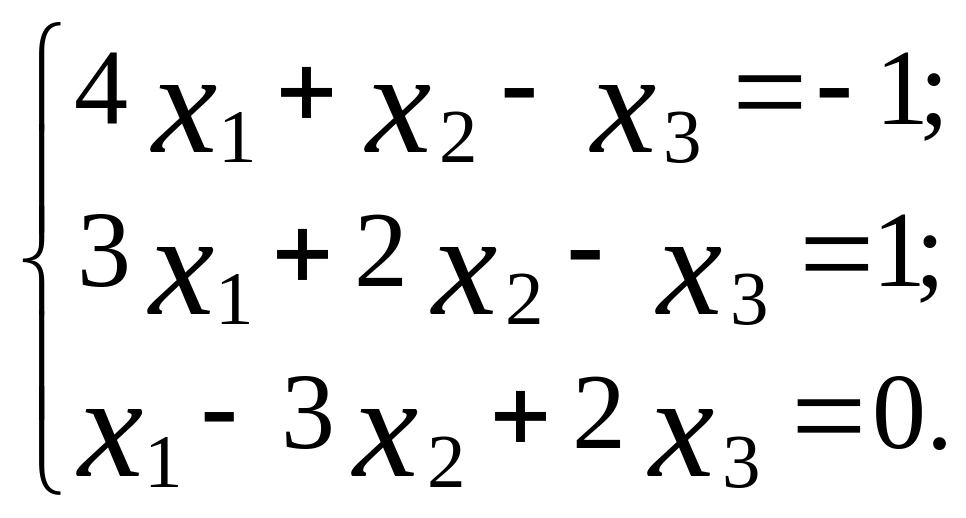 16
16
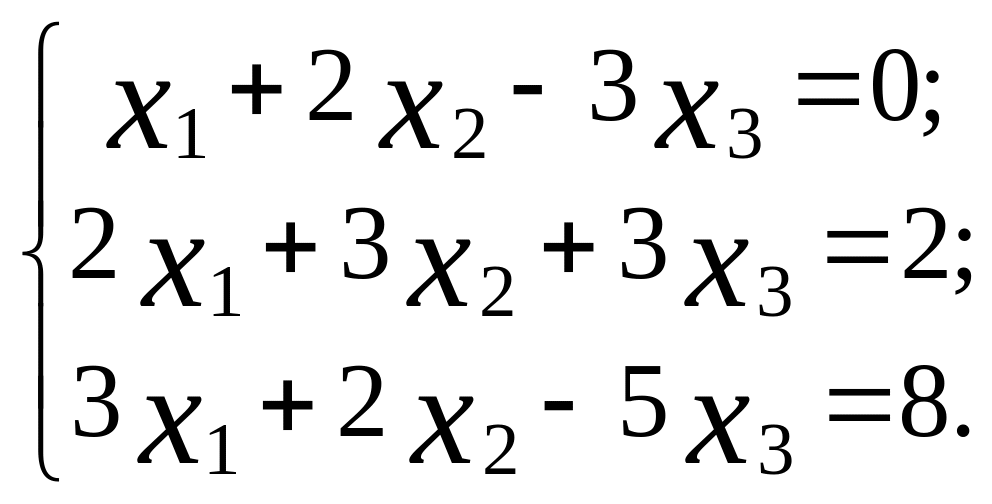
17
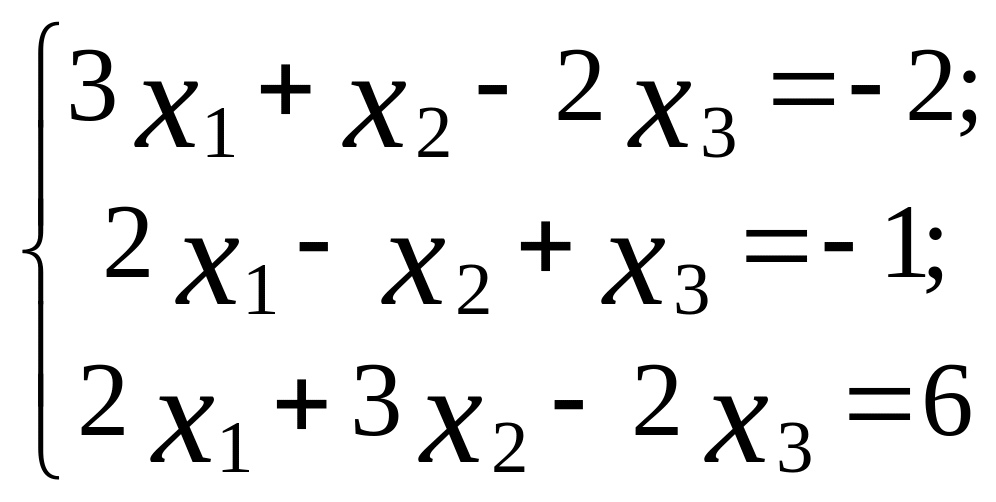 18
18
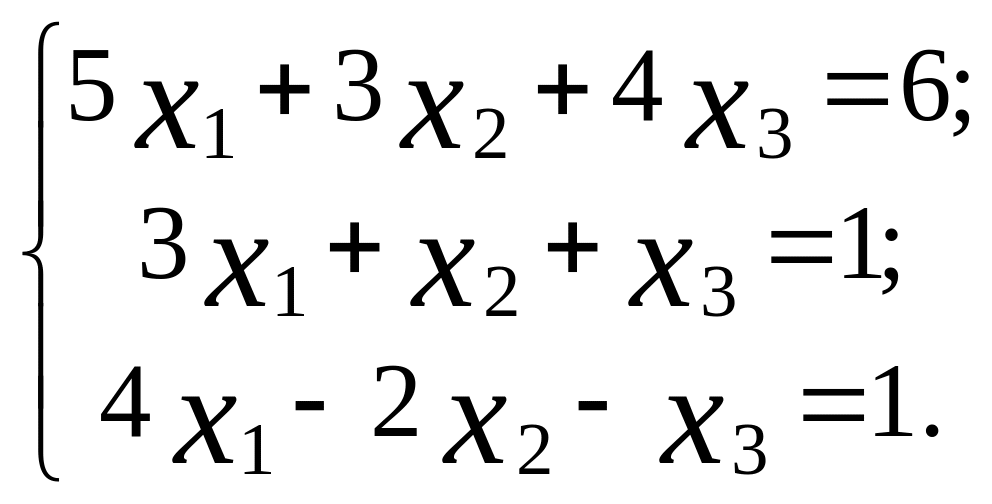
19 20
20

21
 22
22

23
 24
24

25
 26
26

27
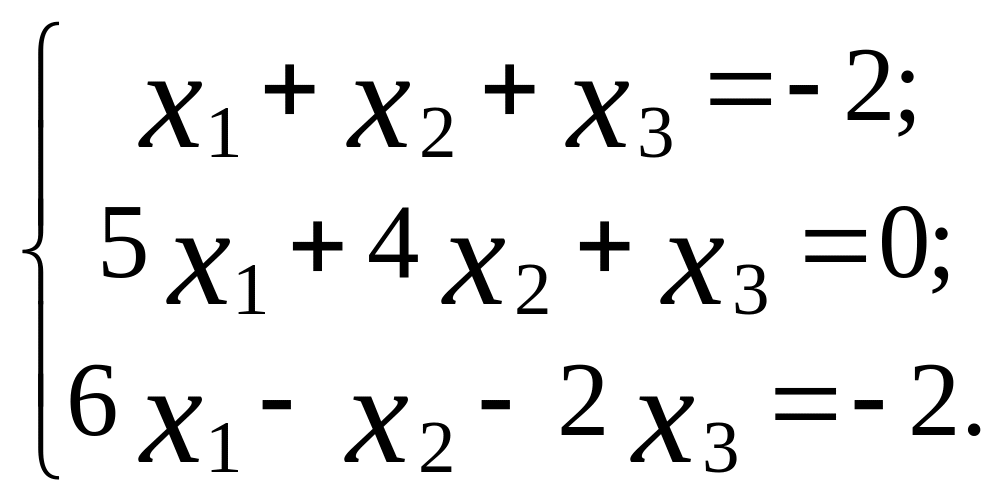 28
28

29
 30
30

31

б) розв’язати матричне рівняння.
1
![]() .
2
.
2
![]() .
.
3
![]() .
4
.
4
![]() .
.
5
![]() .
6
.
6
![]() .
.
7
![]() .
8
.
8
![]() .
.
9
![]() .
10
.
10
![]() .
.
11
![]() .
12
.
12
![]() .
.
13
![]() .
14
.
14
![]() .
.
15
![]() .
16
.
16
![]() .
.
17
![]() .
18
.
18
![]() .
.
19
![]() .
20
.
20
![]() .
.
21
![]() .
22
.
22
![]() .
.
23
![]() .
24
.
24
![]() .
.
25
![]() .
26
.
26
![]() .
.
27
![]() .
28
.
28
![]() .
.
29
![]() .
30
.
30
![]() .
.
31
![]() .
.
Завдання 3 Векторна алгебра
Задача 1
Задані
вектори
![]() =
( а1,а2,а3),
=
( а1,а2,а3),
![]() =(
b1,b2,b3),
=(
b1,b2,b3),
![]() =
( с1,с2,с3).
=
( с1,с2,с3).
Визначити:
1) довжину вектора ;
2) скалярний добуток векторів та ;
3) косинус кута між векторами та ;
4)
векторний добуток векторів
та
;
sin
![]()
5) площу паралелограма та площу трикутника, побудованих на векторах та ;
6)
мішаний добуток векторів![]() ,
,
;
,
,
;
7) об'єм паралелепіпеда та об'єм трикутної піраміди, побудованих на векторах , , ;
8) чи колінеарні вектори та ?;
9) чи компланарні вектори , , ? [7, с. 18-20; 9, с. 8-10, с.25, 28-29; 11, с. 15-22].
