ХАРКІВСЬКА ДЕРЖАВНА АКАДЕМІЯ

ЗАЛІЗНИЧНОГО ТРАНСПОРТУ

Елементи лінійної алгебри та аналітичної геометрії

МЕТОДИЧНІ ВКАЗІВКИ І КОНТРОЛЬНІ ЗАВДАННЯ

для студентів – заочників І курсу

спеціальності

“УПРАВЛІННЯ ПРОЦЕСАМИ ПЕРЕВЕЗЕНЬ

На залізничному транспорті”

Харків – 2000 р.

Методічні вказівки розглянуті та рекомендовані до друку на засіданні кафедри вищої математики 27 червня 2000 року, протокол № 12.

Методичні вказівки підготовлено з метою допомоги студентам-заочникам факультету УПП у виконанні запланованої контрольної роботи №1 з вищої математики в І семестрі І курсу.

Завдання, які містить в собі контрольна робота №1, належать до матеріалу лінійної, векторної алгебри й аналітичної геометрії на площині та у просторі.

В заданих методичних вказівках розроблені типові приклади, до яких додані необхідні теоретичні положення, що використовуються при розв’язанні відповідних задач, а також наведені варіанти індивідуальних завдань.

Методичні вказівки можуть бути корисними і для студентів денної форми навчання при вивченні відповідних розділів вищої математики.

Склали:

доценти Юрчак Н.С.,

Єфременко Р.О.

Рецензент

доцент Куліш Ю.В.

Зміст

Завдання 1 ……………………………………… 4

Завдання 2 ……………………………………… 5

Завдання 3 ……………………………………… 11

Завдання 4 ……………………………………… 11

Завдання 5 ……………………………………… 14

Завдання 6 ……………………………………… 14

Завдання 7 ……………………………………… 18

Завдання до контрольної роботи ……………………………………… 22

Список літератури ……………………………………… 29

Завдання 1. Виконати дії над матрицями

, , .

Знайти .

У цьому завданні треба виконати дві лінійні операції - додавання (віднімання) матриць та множення матриці на число, а також множення матриці на матрицю.

Матрицею називається прямокутна таблиця чисел. Позначимо матрицю А розміром (m - число рядків, n - число стовпців) через [a_ij]_mn, де a_ij - елемент i-го рядка та j-го стовпця матриці А.

При множенні будь – якої матриці на число всі ії елементи множать на це число:

А = [ a_ij ]_mn.

Mатриці однакового розміру можна додавати і віднімати, при цьому їх відповідні елементи додаються або віднімаються:

.

Матрицю А можна множити на матрицю В, якщо їх розміри узгоджені: число стовпців першої матриці А дорівнює числу рядків другої матриці В. При цьому добутком АВ є така матриця С, елементи с_ij якої є сумою добутків відповідних елементів і-го рядка матриці А та j-го стовпця матриці В, тобто

,

.

Отже, виконаємо дії над матрицями

.

Проілюструємо обчислення елемента з індексами i=4, j=3: .

Завдання №2. Розв’язати системи трьох лінійних алгебраїчних рівнянь (СЛАР) а), b), с) за формулами Крамера

а)

Дослідження та розв’язок слар за формулами Крамера потребують введення поняття визначника та способів його обчислення.

Ознайомимося спочатку з визначником другого порядку. Розглянемо квадратну таблицю з будь-яких чотирьох чисел a, b, c, d. Утворимо п’яте число за правилом . Воно називається визначником другого порядку, бо створено з таблиці чисел з двома стовпцями та двома рядками, i позначається символом .

Отже, .

Числа a, b, c, d називають елементами визначника.

Приклад: .

Звичайно всі елементи визначника позначають літерою з двома індексами, наприклад a_ij, де i - номер рядка, j - номер стовпця, на перетині яких розташований елемент. Таким чином, визначник другого порядку можна записати у вигляді

.

Далі означимо визначник третього порядку. Він створюється з квадратної таблиці чисел з трьома рядками та трьома стовпцями і обчислюється за формулою:

Формування елементів кожного доданка та його знака легко запам’ятати, використовуючи схему, яка називається правилом трикутника або правилом Саррюса (множники кожного доданка розташовані у вершинах відповідних трикутників):

“ + ” “ - ”

Наприклад,

Перелічимо властивості визначника, які можна застосувати при його обчисленні.

1. Значення визначника не змінюється при його транспонуванні (тобто заміни місцями стовпців та рядків без зміни їх номерів).

2. Знак визначника зміниться на протилежний, якщо поміняти місцями два його паралельні ряди.

3. Визначник, два паралельних ряди якого збігаються, дорівнює нулю.

4. Спільний множник, який міститься в усіх елементах одного ряду, можна винести за знак визначника.

5. Якщо визначник має ряд, який складається з нулів, то він дорівнює нулю.

6. Значення визначника не зміниться, якщо до елементів будь-якого ряду додати елементи паралельного ряду, помножені на одне й те ж саме число, скажімо:

.

Розглянемо ще один спосіб обчислення визначників.

Мінором M_ij елемента a_ij визначника називається визначник, утворений з після вилучення рядка i стовпця з номерами i та j, тобто тих, на перетині яких знаходяться a_ij. Наприклад, якщо

, то ; .

Алгебраїчним доповненням A_ij елемента a_ij визначника є вираз

.

В розглянутому щойно прикладі

; .

Тепер сформулюємо правило обчислення визначників як властивість 7.

7. Визначник дорівнює сумі добутків елементів будь-якого рядка або стовпця на їх алгебраїчне доповнення, наприклад,

.

Цей визначник розкладений за елементами другого рядка, який ми, для зручності, виділили рамкою. Наприклад, обчислимо визначник, розклавши його за елементами першого рядка

Обчислення визначника за цим методом істотно спрощується, якщо у відповідному ряді, за яким розкладається визначник, дістати якомога більше нульових елементів, користуючись властивістю 6.

Повернемося до СЛАР. Для дослідження та розв’язку СЛАР за формулами Крамера запровадимо поняття головного та допоміжних визначників.

Головним визначником СЛАР називається визначник, елементами якого є коефіцієнти при невідомих. Для пропонованої у прикладі 1 системи головний визначник такий: .

На прикладі його обчислення проілюструємо використання можливих способів: а) за допомогою правила трикутника

б) за допомогою розкладання визначника за елементами, наприклад, третього стовпця:

в) за допомогою поєднання властивостей 6 та 7:

.

(перший рядок помножили на (-1) та додали до другого та до третього). Далі всі визначники будемо обчислювати способом в).

Якщо головний визначник СЛАР не дорівнює нулю, система має єдиний розв’язок. Для знаходження його побудуємо допоміжні визначники СЛАР. Допоміжні визначники створюються з головного визначника заміною його - го стовпця стовпцем із правих частин системи рівнянь:

* - третій стовпець помножили на (-1) та додали до першого;

- за властивістю 3 визначників, оскільки другий та третій рядки збігаються;

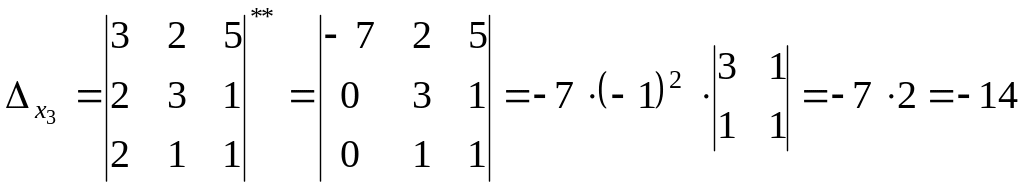
** - третій стовпець помножили на (-2) та додали до першого.

Формули Крамера, за якими знайдемо розв’язки СЛАР, мають вигляд

; ; ,

тобто х₁ = 8/2 = 4; x₂ = 0; x₃ = -14/2 = -7.

Зробимо перевірку та запишемо відповідь

Відповідь: х₁ = 4; х₂ = 0; х₃ = -7.

b)

Відповідно до порядку дій, які описані вище, обчислимо головний визначник

(* - третій рядок помножили на (-1) та додали до другого, третій рядок помножили на (-2) та додали до першого).

Якщо головний визначник СЛАР дорівнює нулю, то система потребує подальшого дослідження.

Обчислимо допоміжні визначники

;

;

.

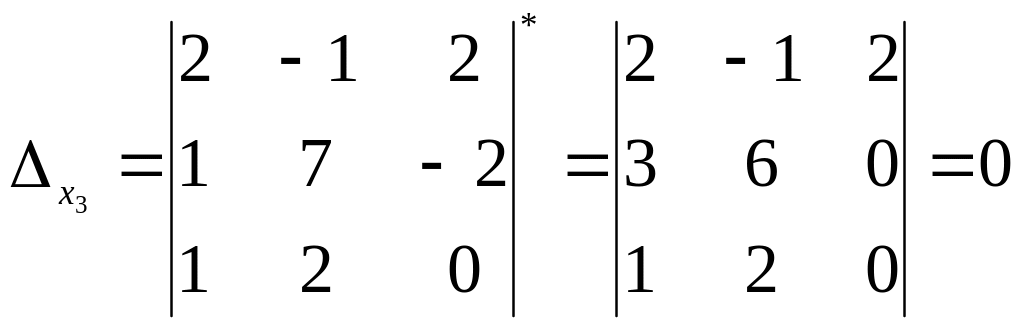(* - перший рядок додаємо до другого; нагадаємо також, що визначник дорівнює нулю, коли його два паралельні ряди пропорційні).

Якщо та всі допоміжні визначники дорівнюють нулю , то СЛАР невизначена, тобто має нескінченну множину розв’язків, або несумісна.

Спробуємо знайти ці розв’язки. З цією метою виключимо одне з рівнянь, наприклад, друге, оскільки у випадку б) одне з рівнянь є наслідком двох інших, та перепишемо систему у вигляді

Надаємо невідомому x₃ довільне значення C, тобто покладемо x₃=C. Система набуває вигляду

При такій формі запису її можна тлумачити як систему двох рівнянь з двома невідомими, головний та допоміжний визначники якої дорівнюють:

,

тоді за формулами Крамера . Це і є розв’язок початкової системи, який називають загальним, бо він містить довільну сталу С.

Будь-який частинний розв’язок отримаємо, якщо надамо С конкретного значення, наприклад С = -1, тоді х₁ = 1; х₂ = -3, х₃ = -1. Перевірка демонструє правильність отриманого розв’язку

Відповідь: .

с) 

(* - перший рядок помножили на (-2) та додали до другого).

Як бачимо, , продовжимо дослідження.

(* - перший стовпець помножили на (-1) та додали до другого).

Таким чином, перший же з допоміжних визначників . Випадок, коли головний визначник системи дорівнює нулю, а хоча б один із допоміжних не дорівнює нулю, відповідає висновку про несумісність СЛАР, тобто система с) не має розв’язків.

Відповідь: система несумісна.

Завдання 3. Розв’язати однорідну систему трьох лінійних алгебраїчних рівнянь за формулами Крамера

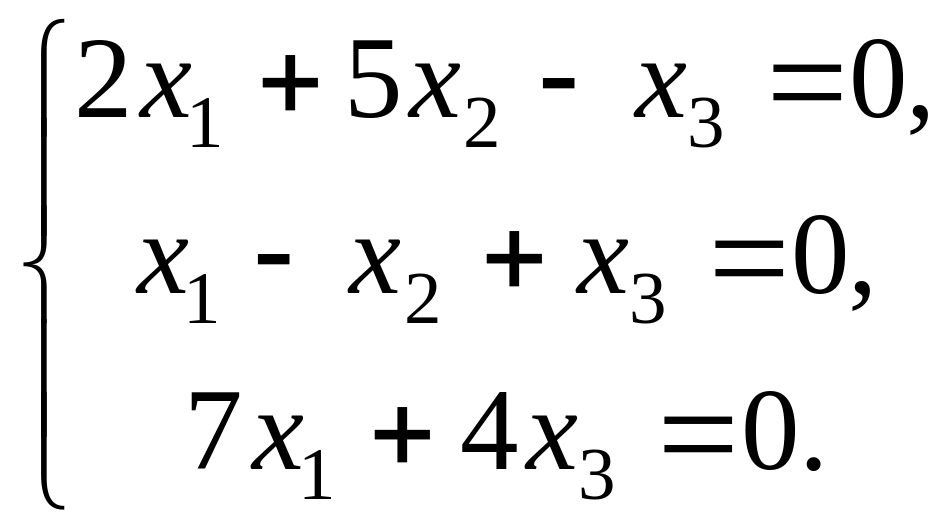
СЛАР називається однорідною, якщо всі праві частини дорівнюють нулю. Однорідна система є окремим випадком неоднорідної, яку ми розглянули у прикладі 1.

Звичайно однорідна СЛАР має нульовий (тривіальний) розв'язок ( ). І якщо головний визначник системи , то цей розв'язок є єдиним (відповідно до дослідження, яке проведено у прикладі 1).

Але якщо , то система має нескінченну множину розв'язків, тому що несумісною у даному випадку вона бути не може (тривіальний розв'язок існує завжди). Ці розв'язки знаходяться так само, як у прикладі 1 b).

Отже, сформуємо головний визначник системи та обчислимо його

.

(* - другий рядок помножили на 5 та додали до першого; ** - визначник дорівнює нулю за властивістю 3).

Таким чином, система має нескінченну множину розв'язків. Знайдемо їх, для чого виключимо, наприклад, перше рівняння, невідому x₃ перенесемо у праву частину та надамо їй довільного значення x₃=C. Після чого система має вигляд

Застосуємо правило Крамера

; ; .

За формулами Крамера отримаємо відповідь:

; ; .

Завдання 4. Розв’язати систему лінійних алгебраїчних рівнянь способами матричного числення

Використовуючи правила матричної алгебри, надамо системі вигляду матричного рівняння

,

де А - матриця коефіцієнтів при невідомих; Х та В - відповідно матриці - стовпці невідомих та правих частин:

.

Обчислимо визначник матриці А, тобто визначник, що складається з елементів матриці А, і який позначають det A:

(* - перший рядок помножили на (-1) та додали до другого; перший рядок помножили на(-2) та додали до третього).

Оскільки , то квадратна матриця А невироджена і тому має обернену матрицю А^-1, а розв’язок системи можна записати у вигляді

Оберненою до невиродженої матриці А називається матриця А^-1, якщо

,

де Е – одинична матриця (квадратна матриця, всі елементи головної діагоналі якої є одиниці, а решта - нулі).

Обчислимо А^-1:

а) знайдемо алгебраїчні доповнення елементів матриці А

б) збудуємо матрицю , змінюючи елементи матриці А на їхні алгебраїчні доповнення:

в) транспонуємо матрицю (поміняємо місцями рядки зі стовпцями, зберігаючи їх номери):

г) помножимо цю матрицю на число , тобто кожний елемент матриці розділимо на det A і отримаємо обернену матрицю:

, або .

Перевіримо правильність здобутої матриці А^-1 за допомогою її означення

.

При цьому, оскільки матриця множиться на матрицю A, то зручніше використовувати її в попередньому вигляді:

,

отже, обернена матриця побудована правильно.

Зрештою знайдемо розв’язок системи за формулою .

Звідси x₁ = 1, x₂ = -1, x₃ = 2.

Зробимо перевірку

Відповідь: х₁ = 1; х₂ = -1; х₃ = 2.

Завдання 5. Побудувати на площині область розв’язків системи лінійних нерівностей

Розв’язуючи кожну нерівність відносно y, отримаємо

На площині розв’язкам (х, у) кожної нерівності відповідають точки, які розташовані вище (у випадку знака >), чи нижче прямих (у випадку знака <) , які є межами наданих областей.

Ці частки площин показані заштрихованими на рисунку.

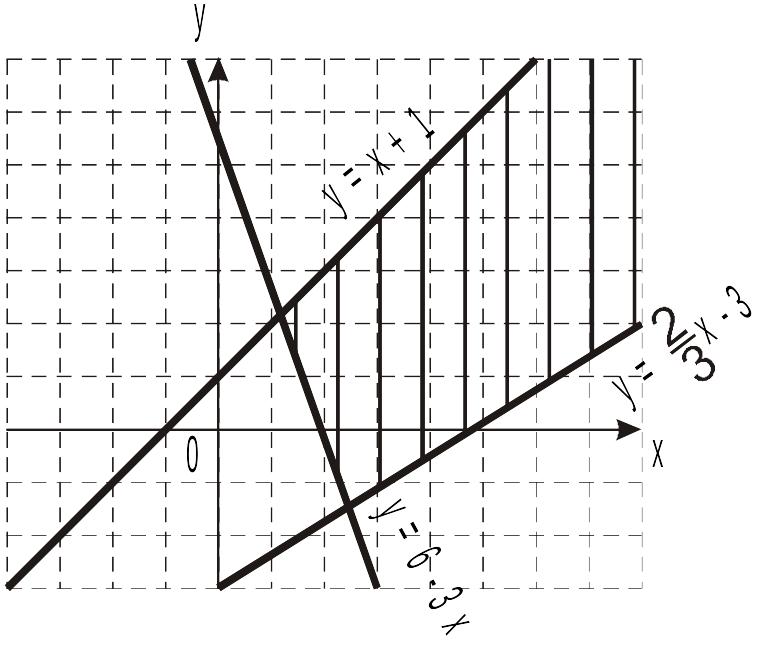
Розв’язком системи нерівностей є частина площини, де перетинаються три заштриховані області.

Завдання 6. Привести до канонічного вигляду рівняння кривої другого порядку а), b), с) та побудувати криву

а) .

Канонічні рівняння основних кривих другого порядку мають вигляд

- коло; - еліпс;

- гіпербола; - парабола,

де (х₀, у₀) - координати центра (для параболи - вершини) відповідної кривої; R - радіус кола; а, b - велика та мала півосі еліпса чи дійсна та уявна півосі гіперболи; p - параметр параболи.

Наявність в кожній формулі повних квадратів, тобто виразів типу (x - x₀)², (y - y₀)² надає змогу визначити перебіг дій для виконання завдання. Він базується на операції виділення повних квадратів, що демонструється у даному прикладі.

Згрупуємо окремо члени з двома різними змінними

.

Винесемо за дужки коефіцієнт при старшому степені x та y

.

У кожному виразі в дужках додамо і віднімемо сталу, яка доповнює відповідний вираз до повного квадрата

.

За формулами для квадратів суми та різниці дістанемо

.

Вільний член перенесемо до правої частини рівняння:

.

Поділимо обидві частини рівняння на 5 (щоб справа отримати одиницю)

.

Одержали рівняння еліпса з центром у точці C , великою піввіссю та малою піввіссю .

Побудуємо цю криву. Для цього на площині xoy зобразимо точку C і проведемо через неї горизонтальну та вертикальну прямі. На горизонтальній прямій від точки C вліво та вправо відкладемо півосі . Це будуть дві вершини еліпса. На вертикальній прямій від точки C уверх та униз відкладемо півосі . Матимемо ще дві вершини еліпса. Через отримані вершини проводимо еліпс.

b) .

Проводимо дії за описаним у попередньому прикладі способом

.

Таким чином, рівняння b) є рівнянням гіперболи з центром у точці С (-2; 1), дійсною піввіссю та уявною піввіссю (оскільки знак “-“ у рівнянні стоїть перед членом, що містить поточну координату Y).

Для побудування гіперболи позначимо точку C (-2; 1) на площині XOY та проведемо через цю точку горизонтальну та вертикальну прямі. На горизонтальній прямій відкладемо ліворуч та праворуч від точки C відрізок , на вертикальній – відрізок уверх та униз. Будуємо прямокутник зі сторонами, які проходять через отримані чотири точки паралельно до осей координат. Діагоналі прямокутника є асимптотами гіперболи, тобто прямими, до яких наближаються гілки гіперболи. Вершини гіперболи розташовані на дійсній осі.

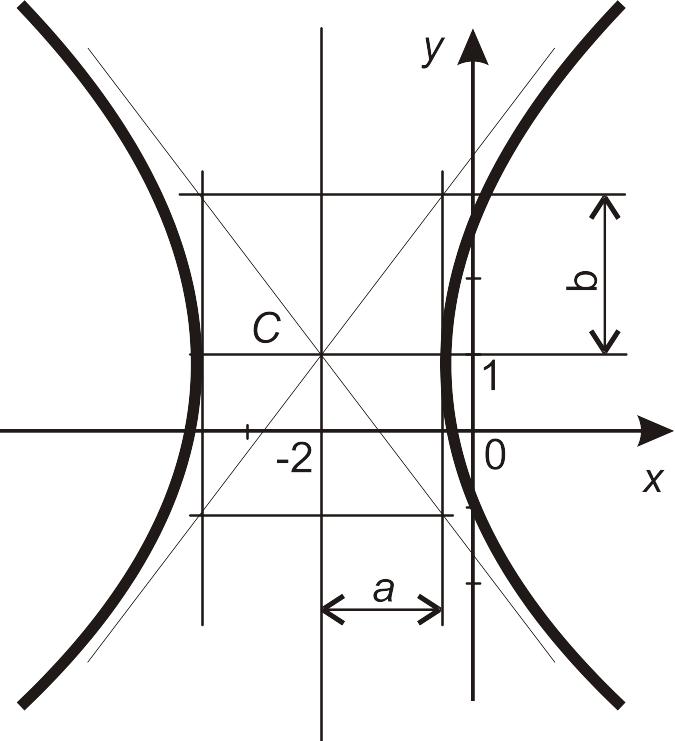
с)

Це рівняння відрізняється від попередніх наявністю в ньому тільки однієї змінної у другій степені, що є ознакою рівняння параболи. Зробимо всі вже відомі дії та отримаємо його канонічний вигляд

,

,

.

Таким чином, вершина параболи знаходиться в точці C (3; -1), параметр p=1, ось симетрії проходить через т. С паралельно осі ординат. Для побудування параболи варто відмітити точки перетину з осями координат: ; ; ;