Тема 8.2. Первая и вторая теоремы двойственности

Теоремы двойственности позволяют установить взаимосвязь межу оптимальными решениями пары двойственных задач. Решив одну из пары двойственных задач, можно или найти оптимальное решение другой задачи, не решая ее, или установить его отсутствие.

Возможны следующие случаи:

1. Обе задачи из пары двойственных имеют оптимальные решения.

2. Одна из задач не имеет решения в виду неограниченности целевой функции, а другая не имеет решения в виду несовместности системы ограничений.

Теорема 1. Если одна из пары двойственных задач имеет оптимальное решение, то и двойственная к ней имеет оптимальное решение, причем значение целевых функций задач на своих оптимальных решениях совпадают.

Если одна из пары двойственных задач не имеет решения в виду неограниченности целевой функции, то другая не имеет решения в виду несовместности системы ограничений.

Пусть имеется симметрическая пара двойственных задач:

Теорема 2. Для того чтобы решения и являлись оптимальными решениями пары двойственных задач, необходимо и достаточно, чтобы выполнялись следующие равенства

Иначе, если при подстановке оптимального решения в систему ограничений i–ое ограничение исходной задачи выполняется как строгое неравенство, то i-ая координата оптимального решения двойственной задачи равна нулю, и , наоборот, если i–ая координата оптимального решения двойственной задачи отлична от нуля, то i–ое ограничение исходной задачи удовлетворяется оптимальным решением как равенство.

Пример. Составить двойственную задачу к исходной.

Задача А	Переменные, соответст-вующие ограниче-ниям задачи А.	Переменные, соответст-вующие ограниче-ниям задачи В.	Задача В (двойственная к задаче А)

Тема 9. Транспортная задача

Пусть имеется m поставщиков А₁, А₂, …А_m однородного груза в количества а1, а2, а m единиц и n потребителей B_1, В₂, …В_n этого груза, потребность которых составляет соответственно b₁,b₂, b_n единиц.

Известны стоимости перевозок единицы груза от i-го поставщика к j-му потребителю

с_ij (i=1, 2,…m, j=1,2,…n).

Требуется составить такой план перевозок, который обеспечит минимальные транспортные расходы.

Исходные данные транспортной задачи записываются в виде таблицы.

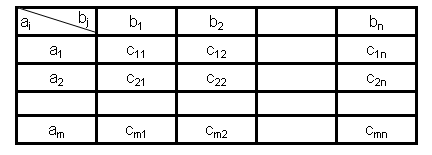
Переменные х_ij (i=1, 2,…m, j=1,2,…n) – объемы перевозок от каждого от i-го поставщика к j-му потребителю. Эти переменные могут быть записаны в виде матрицы перевозок.

Тема 9.1. Экономико-математическая модель транспортной задачи

Математическая модель транспортной задачи в общем случае имеет вид:

Целевая функция задачи (А) выражает требование обеспечить минимум суммарных затрат на перевозку всех грузов. Группа из m уравнений (В) описывает тот факт, что запасы всех m поставщиков вывозятся полностью. Вторая группа из n уравнений (С) выражает требование полностью удовлетворить запросы всех n потребителей. Неравенство (D) является условиями неотрицательности всех переменных задачи.

Таким образом математическая формулировка транспортной задачи состоит в следующем:

Найти матрицу Х =( х_ij ) i=1, 2,…m, j=1,2,…n, элементы которой удовлетворяют системе ограничений (В) и (С), условиям неотрицательности (D) и обеспечивают минимум целевой функции (А).

В рассматриваемой модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарным запросам потребителей т.е.

(Е)

Такая задача называется задачей с правильным балансом, а её модель закрытой. Если это равенство не выполняется, то модель называется задачей с неправильным балансом, а её модель – открытой.