Тема 7.2. Метод искусственного базиса
Пусть задача линейного программирования задана в канонической форме
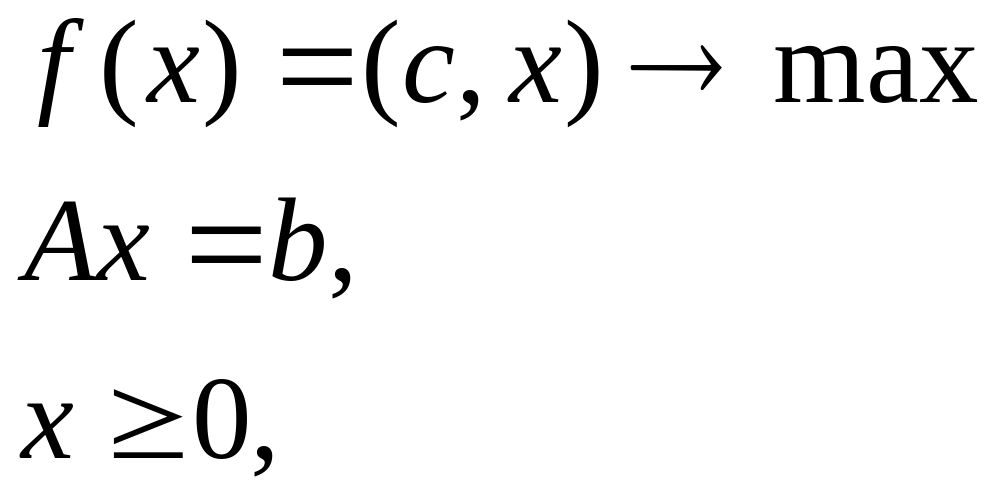и b≥0. (1)
Пусть матрица A не содержит m единичных ортов. Тогда для определения начального опорного плана используется метод искусственного базиса. Для этого рассмотрим вспомогательную задачу
и b≥0
(2)
Очевидно, что вектор
является опорным решением задачи (2).
Справедливы утверждения:
Утверждение 1. Задача (2) всегда
разрешима и
.
Утверждение 2. Если
,
то система ограничений задачи (1)
противоречива.
Утверждение 3. Если
,
и вектор
-оптимальный
опорный план задачи (2), то вектор
является опорным планом задачи (1).
При этом из оптимальной симплекс-таблицы задачи (2) можно построить начальную симплекс-таблицу задачи (1).
Пример. Решить задачу линейного программирования симплексным методом.
Приводим задачу к каноническому виду:
Запишем коэффициенты при переменных в системе ограничений:
В качестве базисных переменных выбираем переменные, имеющие единичный вектор-столбец. В нашем примере базисные переменные- x3 и x4, остальные переменные небазисные. Полагая небазисные переменные равные нулю, находим значения базисных переменных.
Х1=0, Х2=0, Х3=6, Х4=9, f=0.
уравнение |
Базисные переменные |
Свободные. члены |
Х1 |
Х2 |
Отношение |
0 |
f |
0 |
-1 |
-1 |
|
1 |
Х3 |
6 |
2 |
1 |
6:2 =3 (min) |
2 |
Х4 |
9 |
2 |
3 |
9:2=4,5 |
В 0-ой строке есть коэффициенты <0, выбираем наименьший, например, Х1 –это будет ведущий столбец.
Для определения ведущей строки рассматриваем положительные отношения столбца свободных членов к элементам ведущего столбца.
Х1→ вводим в базис. Х3→выводим из базиса.
Из ведущей строки выражаем Х1 и подставляем в уравнение 0 и 2.
Подставим выражение для Х1 в уравнение 2 и 0.
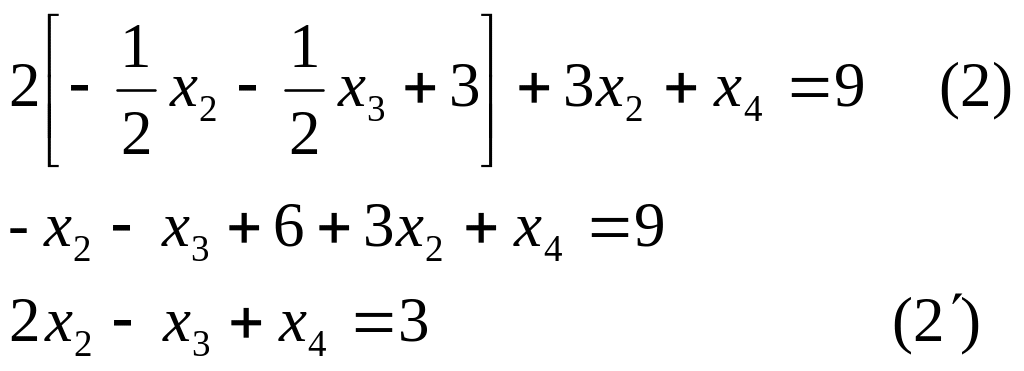
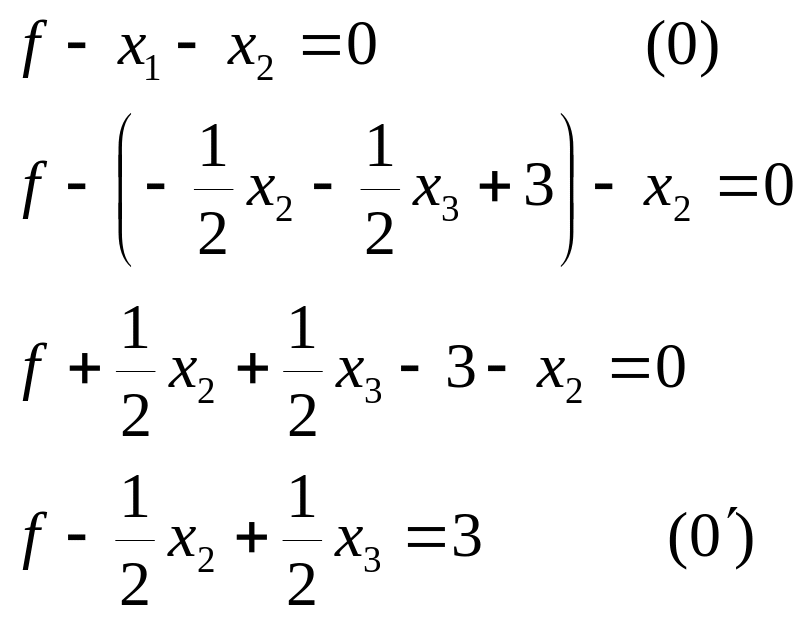
Х2=0, Х3=0, Х1=3,Х4=3, f=3.
уравнение |
Базисные переменные |
Свободные. члены |
Х2 |
Х3 |
Отношение |
0 |
f |
3 |
-1/2 |
1/2 |
|
1 |
Х1 |
3 |
1/2 |
1/2 |
3:1/2 =6 |
2 |
Х4 |
3 |
2 |
-1 |
3:2=3/2(min) |
Х2→ вводим в базис. Х4→выводим из базиса.
Из ведущей строки выражаем Х2 и подставляем в уравнение 1 и 0.
Х1=9/4, Х2=3/2, Х3=0,Х4=0, f=15/4.
f*(9/4,3/2,0,0)=15/4
уравнение |
Базисные переменные |
Свободные. члены |
Х3 |
Х4 |
Отношение |
0 |
f |
15/4 |
1/4 |
1/4 |
|
1 |
Х1 |
9/4 |
3/4 |
-1/4 |
|
2 |
Х2 |
3/2 |
-1/2 |
1/2 |
|