Методичні вказівки

з курсу «Економіко-математичне моделювання»

до лабораторної роботи №2

«Симплекс-метод у лінійному програмуванні»

Заняття 3

Символьні обчислення та рішення рівнянь у системі MathCad2000

1. Мета роботи

1. Вивчення можливостей символьних перетворень у системі MathCAD.

2. Вивчення можливостей рішення різних типів рівнянь й їхніх систем у системі MathCAD.

  

2. Завдання роботи

1. Освоїти прийоми роботи із системою MathCAD.

2. Освоїти способи рішення різних типів рівнянь й їхніх систем аналітичними й чисельними методами в середовищі MathCAD.

 

3. Зміст роботи

3.1 Запустити додаток MathCAD.

3.2 Освоїти роботу з розділом Символи. По черзі включити кілька пунктів даного розділу, ознайомитися із принципом їхнього розташування й виклику їхніх опцій.

3.3 Повторити всі наведені у вказівках приклади.

3.4. Освоїти способи рішення рівнянь в аналітичній формі. 

3.5. Вирішити задачу лінійного програмування за допомогою функцій Minimize, Maximize (Додаток В).

3.6. Зберегти результати у файлі із введенням необхідних коментарів й оформити звіт.

 

4. Вимоги до звіту

Звіт повинен містити:

- назва роботи, постановку завдання дослідження;

- результати обчислень, а також відомості про послідовності її виконання;

- результати обчислень без допомоги ПК, а за допомогою симплекс методу;

- відповіді отримані у результаті симплекс методу та отримані за допомогою роботи системі MathCAD порівняти, зробити належні висновки;

- відповіді на контрольні питання за вказівкою викладача.

 

5. Загальні положення

Меню символьних засобів Символи

 За допомогою пункту Символи головного меню викликається падаюче меню символьних засобів (Рис. 1), з них частина містить свої підменю (Рис. 2).

Зміст представлених функцій досить очевидний. Розглянемо деякі з них.

Рис. 1

Щоб символьні операції виконувалися, необхідно вказати, над яким вираженням ці операції повинні вироблятися, тобто треба виділити вираження (правила виділення описувалися вище). Потім вибрати в головному меню.

Для ряду операцій варто не тільки вказати вираження, до якого вони ставляться, але й намітити змінну, щодо якої виконується та або інша символьна операція. Саме вираження в такому випадку не виділяється, адже й так ясно, що якщо маркер уведення виділяє змінну якого-небудь вираження, та це вираження вже відзначене наявністю в ньому виділеної змінної.

 

Рис. 2

Символи/Спростити - спростити виділене вираження з виконанням таких операцій, як скорочення подібних що складають, приведення до загального знаменника, використання основних тригонометричних тотожностей і т.д. Дана операція дозволяє спрощувати математичні вираження, що містять алгебраїчні тригонометричні функції, а також вираження зі статечними багаточленами (поліномами). З його допомогою можна спростити складні й погано впорядковані алгебраїчні вираження.

Розкладання математичних виразів.

Дія пункту меню Розширити падаючого меню Символи головного меню MathCad у відомому змісті протилежно дії пункту Спростити. За допомогою пункту Розширити більше складні функції перетворяться через більше прості. Алгебраїчні вирази, представлені в стислому виді, зводяться до розгорнутого й т.д.

Диференціювання математичних виразів.

Пункт Диференціювання спливаючого меню Змінні (Рис. 2) дозволяє диференціювати вирази щодо виділеної змінної. Він повертає символьне значення похідної вираження по тій змінній, котра виділена курсором. Для обчислення похідних вищого порядку потрібно повторити обчислення необхідне число раз. Нижче наведений фрагмент документа з обчисленням похідної (Рис. 3).

 

Рис. 3

  Диференціювати функцію можна і за допомогою пункту Панель інструментів спливаючого меню Вид, в якому виділити меню Математика (Рис.4). З’явиться спливаюче меню (рис.5), з якого вибирається похідна першого або іншого порядку.

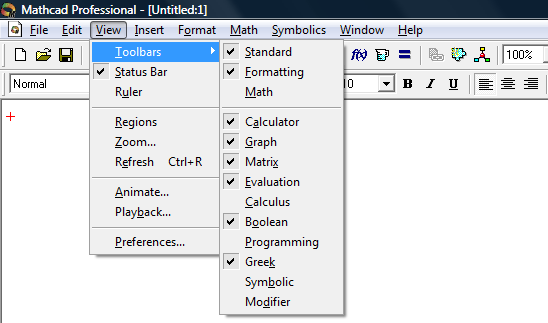
  Рис.4

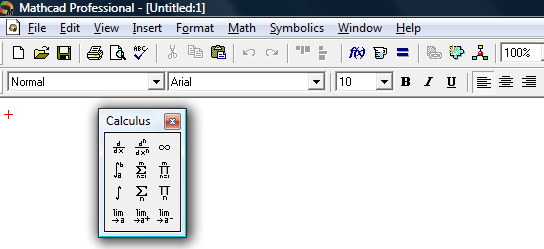
Рис.5

Приклад

Знайти частинні похідні функції .

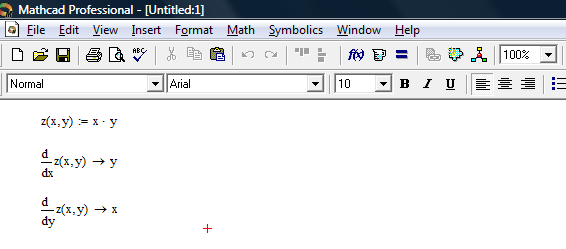
Рис.6

Інтегрування математичних виразів.

Пункт Інтегрування спливаючого меню Змінні (Рис. 2) дозволяє призначений для інтегрування вираження по виділеній змінній. Для необхідного перетворення вводиться тільки функція, яка знаходиться під знаком інтегралу. Нижче наведений фрагмент документа з обчисленням інтеграла (Рис. 7).

 

Рис. 7

Рішення рівнянь в аналітичній формі.

Система MathCad дозволяє вирішувати лінійні, нелінійні рівняння й системи рівнянь як аналітично, так і чисельно й графічно. Ці функції здійснюються в такий спосіб. Пункт Змінні падаючого меню пункту Символи головного меню MathCad викликає спливаюче меню (Рис. 8).

 

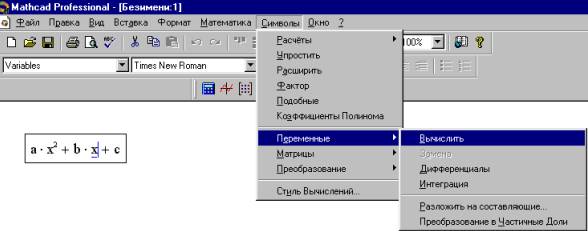
Рис. 8

  

За допомогою пункту спливаючого меню Обчислити рівняння (нерівність) вирішується щодо виділеної змінної, тобто виробляється пошук такого значення зміної, при якому вихідне вираження стає рівним нулю. На рисунку 9 представлений приклад рішення квадратного рівняння.

 

 

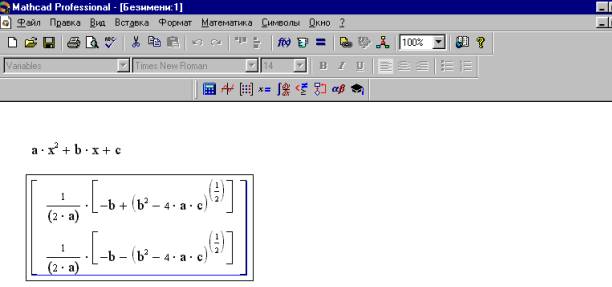
Рис. 9

  Інший спосіб рішення рівнянь можна здійснити, скориставшись панеллю символьних обчислень , на якій необхідно вибрати кнопку . Після чого з'явиться на екрані повідомлення .

Уведіть у позначеній позиції ліворуч від ключового слова solve вираження для правої частини рівняння, а в позиції праворуч від solve – ім'я змінної, щодо якої потрібно вирішити рівняння, і клацніть по вільному місцю в робочому документі. Результат (значення кореня рівняння) буде відображений у робочому документі праворуч від стрілки (Рис. 10).

 

Рис. 10

  

Багато нелінійних рівнянь, наприклад трансцендентні, і системи з них не мають аналітичних рішень і вирішуються графічними або чисельними методами.

Функція root(вираження, ім'я змінної) шукає значення змінної, при якій вираження стає рівним нулю. Пошук кореня здійснюється ітераційними методами, причому перед цим треба задати початкове значення х.

Приклад Наближене рішення рівнянь

 

 

Якщо необхідно знайти рішення рівняння з декількома змінними або системи рівнянь, задається блок рівнянь. Він має наступну структуру:

- Given – службове слово, що відзначає початок блоку;

- рівняння;

- обмежувальні умови;

- вираження з функціями Find, Minerr, Maximize, Minimіze;

- перевірка рішення (якщо необхідно).

У цьому випадку використаються наступні функції:

а) Find(х₁,х₂,…,х_n) – повертає значення однієї змінної або значення вектора змінних Х, що відповідає точному рішенню.

б) Minerr(х₁,х₂,…,х_n) – повертає значення одного змінної або значення вектора змінних Х, що відповідає наближеному рішенню з мінімальної середньоквадратичною похибкою.

в) Maximize (f,х₁,х₂,…,х_n) – повертає максимальне значення цільової функції та значення однієї змінної або значення вектора змінних Х.

г) Minimіze(f,х₁,х₂,…,х_n) – повертає мінімальне значення цільової функції та значення однієї змінної або значення вектора змінних Х.

Обмежувальні умови служать для обмеження області рішення за допомогою функції Find або мінімізації середньоквадратичної похибки за допомогою функції Minerr.

Для завдання початкового значення, щоб уникнути тривіальних помилок, можна побудувати графік досліджуваної функції. Задайте в робочому документі функцію f(x) і побудуйте її графік у декартових координатах. Щоб знайти графічно корінь рівняння – абсциси точок перетинання графіка функції з віссю ординат, клацніть по полю графіка правою кнопкою миші. У контекстному меню, що з'явився, виберіть пункт Трасування й установіть (стрілками клавіатури або мишею) маркер (перехресні пунктирні лінії) у точці перетинання графіка функції з віссю абсцис. У вікні діалогу відображаються координати маркера: значення координати х при рівності координати y нулю або малій величині і є шукане наближене значення кореня (Рис. 4).

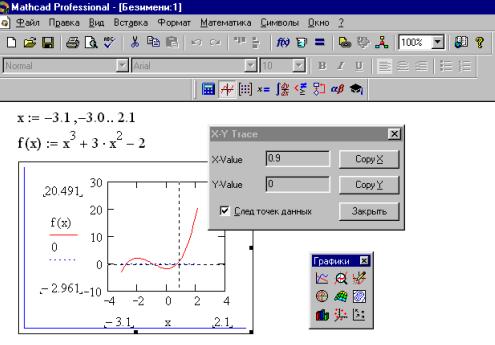
Рис. 11 

 

Вирішення задач лінійного програмування за допомогою  MathCAD.

Приклад.

Розв’язати задачу лінійного програмування.

при заданих обмеженнях

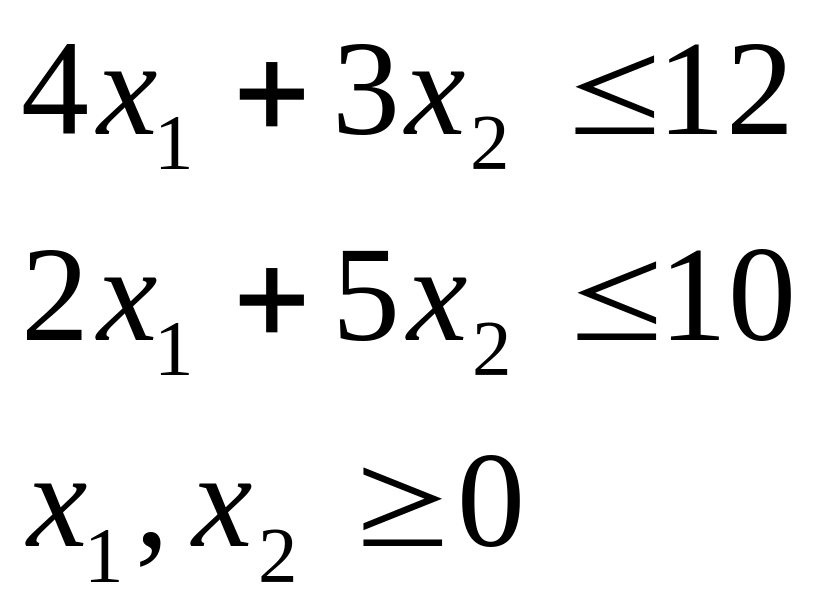
Ця задача може бути розв’язана без використання комп’ютера за допомогою прямого симплекс методу. А у системі MathCAD розв’язок має такий вигляд:

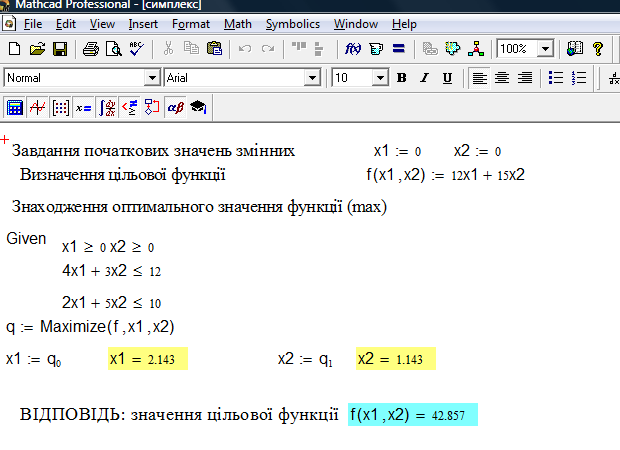
Рис.12

Аналогічно знаходиться мінімум функції за допомогою встроєної функції MathCAD – Minimize.

Заняття 4

ЗНАЙОМСТВО ІЗ СИСТЕМОЮ ЕЛЕКТРОННИХ ТАБЛИЦЬ Excel,

ФОРМУВАННЯ ТАБЛИЦІ. РІШЕННЯ ЗАДАЧІ ЛІНІЙНОГО ПРОГРАМУВАННЯ.