Тема 17. Поверхности второго порядка

Таблица 17.1. Краткие сведения о поверхностях второго порядка

Вещественный эллипсоид	Мнимый эллипсоид
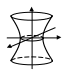
Однополостный гиперболоид	Двуполостный гиперболоид
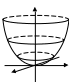
Эллиптический параболоид	Гиперболический параболоид
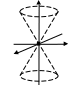
Вещественный конус	Мнимый конус (точка)

Девять цилиндров, соответствующих девяти кривым второго порядка

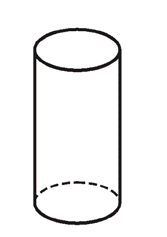
Эллиптический цилиндр	Прямая линия (две мнимые пересекающиеся плоскости)	Мнимый эллиптический цилиндр
Гиперболический цилиндр	Две пересекающиеся плоскости	Параболический цилиндр
Две параллельные плоскости	Две совпадающие плоскости	Две мнимые параллельные плоскости

Задачи к теме 17

Во всех задачах этой темы система координат – прямоугольная.

17.1(941). Определить координаты центра и найти радиус каждой из следующих сфер:

1) ;

2) ;

3) ;

4) .

17.2(945). Найти центр и радиус окружности

,

.

17.3(976). Написать уравнение круглого цилиндра, проходящего через точку (1, –2, 1), осью которого служит прямая

.

17.4(977*). Составить уравнение цилиндра, описанного вокруг сферы зная направляющий вектор образующих цилиндра.

17.5(984*). Составить уравнение поверхности круглого конуса, вершина которого находится в точке (1, 2, 3), направляющий вектор оси , а угол образующих конуса с его осью равен .

17.6(1022). Написать уравнение поверхности второго порядка, проходящей через три окружности

, ;

, ;

, ,

и привести полученное уравнение к каноническому виду.

17.7(1041). Определить вид поверхности и ее расположение относительно начальной системы координат, пользуясь преобразованием левой части ее уравнения:

1) ;

2) ;

3) ;

4) ;

5) .

17.8(1042). Определить вид и расположение поверхности, пользуясь переносом системы координат:

1) ;

2) ;

3) ;

4) .

17.9(1044*). Определить вид поверхности второго порядка и ее расположение относительно исходной системы координат, пользуясь переносом и поворотом системы координат вокруг одной из ее осей:

1) ;

2) ;

3) .

Решения избранных задач

В данном разделе предлагаются решения следующих задач: 1.9, 5.6, 7.1, 7.2, 7.3, 7.4, 7.6(1), 12.14, 12.15.

Задача 1.9

Из точки О выходят два вектора, = , = . Найти какой-нибудь вектор = , идущий по биссектрисе угла АОВ.

Решение

Для решения этой задачи достаточно использовать правило параллелограмма, вспомнив при этом, что диагональ в параллелограмме является биссектрисой, если параллелограмм является ромбом, то есть все его стороны оказываются равными. Поэтому достаточно от векторов и перейти к векторам и , которые направлены также как и , соответственно, но имеют одинаковые длины . В качестве векторов и можно взять орты векторов и : и . Тогда искомое выражение для вектора будет выглядеть следующим образом:

.

Можно предложить и другие решения этой задачи, например:

, и т.д. и т.п.