
- •Лабораторное занятие № 4
- •1. Цель занятия
- •2. Теоретические основы
- •3. Лабораторное оборудование
- •4. Домашнее задание
- •5. Лабораторное задание
- •Решение
- •6. Содержание отчета
- •7. Контрольные вопросы
- •Лабораторное занятие № 5
- •1. Цель занятия
- •2. Теоретические основы
- •2.1. Показатели безопасности
- •2.2. Анализ безотказности и безопасности двухканальных систем
- •3. Лабораторное оборудование
- •4. Домашнее задание
- •5. Лабораторное задание
- •Решение
- •6. Содержание отчета
- •7. Контрольные вопросы
- •Лабораторное занятие № 6
- •1. Цель занятия
- •2. Теоретические основы
- •3. Лабораторное оборудование
- •4. Домашнее задание
- •5. Лабораторное задание
- •6. Содержание отчета
- •7. Контрольные вопросы
- •Рекомендуемая литература
- •Приложение а табличный процессор microsoft excel
- •Приложение б вычисление определителей высших порядков Определитель
- •Содержание
2.2. Анализ безотказности и безопасности двухканальных систем
При построении безопасных микроэлектронных систем обеспечения движения поездов наибольшее применение получили различные варианты двухканальных и трехканальных (мажоритарных) структур. Рассмотрим работу двухканальной (дублированной) системы с безопасным сравнением (рис. 5.2). В ней две одинаковые (равнонадежные) микроЭВМ работают параллельно во времени. Их аналогичные выходные сигналы сравниваются безопасной схемой сравнения (БСС). Сигнал на управление формируется только при совпадении соответствующих сигналов обоих микроЭВМ.
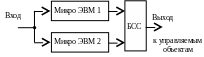
Рис. 5.2
В таблице 5.2 приведены состояния рассматриваемой системы в зависимости от состояний каналов (Р – работоспособное состояние; Н – неработоспособное состояние; З – защитное состояние; О – опасное состояние).
Схема БСС считается абсолютно надежной. Система работоспособна только в том случае, если работоспособны обе микроЭВМ. Это означает, что с точки зрения безотказности мы имеем логически последовательное соединение каналов (см. лабораторное занятие № 2).
Таблица 5.1
Номер состояния (события), i |
Состояние |
Вероятность i – го события (состояния), Ri(t) (безотказность) |
|||
Каналов, Kn |
Системы, S |
||||
МикроЭВМ 1 |
МикроЭВМ 2 |
Безотказность |
Безопасность |
||
0 |
Р |
Р |
Р |
Р |
|
1 |
Р |
Н |
Н |
З |
|
2 |
Н |
Р |
Н |
З |
|
3 |
Н |
Н |
Н |
О |
|
Система переходит в опасное состояние, если неработоспособны обе микро ЭВМ. В этом случае может оказаться, что неправильные значения одноименных выходных сигналов обоих каналов совпадают, и система выдает неправильное воздействие на управляемые объекты. Следовательно, с точки зрения безопасности имеем логически параллельное соединение каналов.
Будем считать, что
показатели безотказности одной микро
ЭВМ (одного канала) распределены по
экспоненциальному закону (по условию:
![]() ):
):
![]() ,
(5.1)
,
(5.1)
![]() ,
(5.2)
,
(5.2)
![]() .
(5.3)
.
(5.3)
Следовательно, показатели безотказности для двухканальной системы (логически последовательное соединение каналов) будут определяться по формулам:
![]() ,
(5.4)
,
(5.4)
![]() ,
(5.5)
,
(5.5)
![]() ,
(5.6)
,
(5.6)
![]() .
(5.7)
.
(5.7)
Показатели безопасности для двухканальной системы (логически параллельное соединение каналов) будут определяться по формулам:
![]() ,
(5.8)
,
(5.8)
![]() ,
(5.9)
,
(5.9)
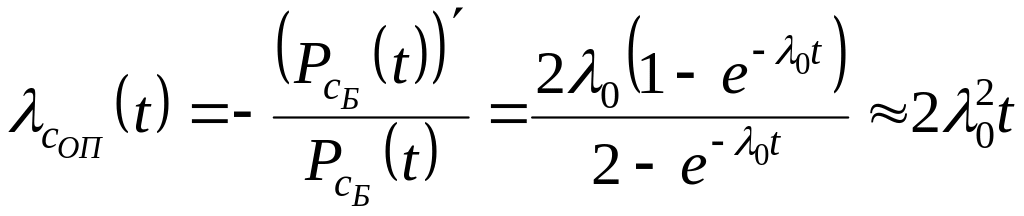 ,
(5.10)
,
(5.10)
![]() .
(5.11)
.
(5.11)
Из формулы (5.10) следует, что интенсивность опасных отказов двухканальной системы является функцией времени, несмотря на то, что интенсивность отказов одного канала является постоянной величиной.
Примечание. При расчете показателей безотказности двухканальной системы был использован универсальный метод расчета надежности любой резервированной системы со сложной логической структурой – метод полной группы событий.
В любой момент
времени t состояние
системы S (в нашем
случае двухканальной системы) определяется
состоянием ее элементов Kn
(в нашем случае – каждого из каналов).
Каждый элемент (канал) может находиться
в одном из двух состояний: Kn=
1, если элемент (канал) работоспособен
(в нашем случае это состояние обозначено
как «Р»), или Kn=
0, если элемент (канал) – неработоспособен
(в нашем случае это состояние обозначено
как «Н»). Всего существует 2n
(n – число элементов
(каналов) системы) состояний системы. В
нашем случае таких состояний (см. таб.
5.1): 2n=22=4
(i=0, 1, 2, 3). Система,
также может находиться в одном из двух
состояний: S = 1,
если система работоспособна (в нашем
случае это состояние обозначено как
«Р»), или S = 0, если
система – неработоспособна (в нашем
случае это состояние обозначено как
«Н»). Состояние системы является функцией
(алгебры логики) от состояния её элементов:
![]() .
В нашем случае (логически последовательное
соединение каналов с точки зрения
безотказности):
.
В нашем случае (логически последовательное
соединение каналов с точки зрения
безотказности):
![]() (или
(или
![]() ).
Так как вероятность безотказной работы
одного элемента (канала) может быть
обозначена как
).
Так как вероятность безотказной работы
одного элемента (канала) может быть
обозначена как
![]() ,
а другого –
,
а другого –![]() ,
то вероятность нахождения системы,
например, в состоянии i=0
будет равна (см таб. 5.1):
,
то вероятность нахождения системы,
например, в состоянии i=0
будет равна (см таб. 5.1):
![]() .
Вероятность безотказной работы
системы будет равна сумме вероятностей
тех событий, в которых система
работоспособна S =
1 (в нашем случае это состояние
обозначено как «Р»):
.
Вероятность безотказной работы
системы будет равна сумме вероятностей
тех событий, в которых система
работоспособна S =
1 (в нашем случае это состояние
обозначено как «Р»):
![]() .
.
Для таблицы 5.1.:
![]() .
.
Учитывая, что в
нашем случае
![]() ,
то:
,
то:
.
