Лабораторное занятие № 4

ТЕМА ЗАНЯТИЯ: ИССЛЕДОВАНИЕ НАДЕЖНОСТИ

ДИСКРЕТНЫХ СИСТЕМ

С ВОССТАНАВЛИВАЮЩИМИ ОРГАНАМИ

1. Цель занятия

1.1. Получить и закрепить теоретические знания по расчету надежности дискретных систем с восстанавливающими органами (ВО).

1.2. Получить практические навыки в решении задач по расчету надежности дискретных систем с ВО с использование ЭВМ.

2. Теоретические основы

Для дискретных устройств характерным видом отказов являются сбои – самоустраняющиеся отказы. Наиболее эффективным способом борьбы со сбоями являются структурное резервирование с дробной кратностью и использование элементов голосования, которые получили название восстанавливающих органов (ВО) или мажоритарных элементов (МЭ) (рис. 4.1).

Рис. 4.1

ВО (МЭ) функционирует согласно следующему уравнению:

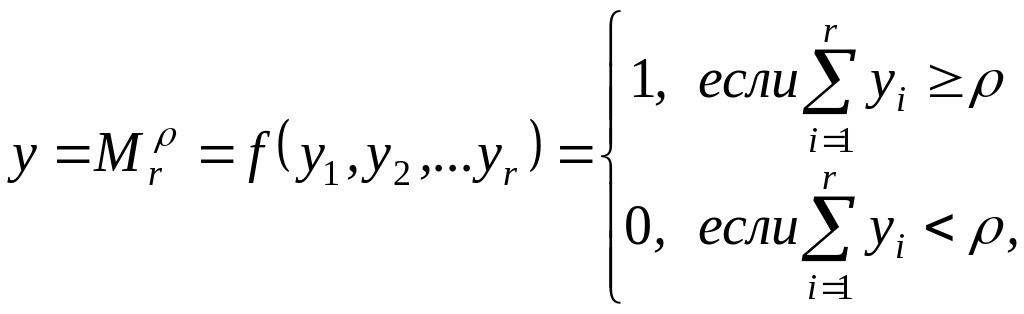(4.1)

где – знак мажоритирования (голосования) из по ;

– порог голосования, т.е. минимальное число единиц на входах ВО, при котором сигнал на выходе y = 1.

– общее число однотипных ДУ (основных и резервных).

Из выражения (4.1) следует:

1. ВО может корректировать ( – ) отказов ДУ типа ложный «0»;

2. ВО может корректировать ( –1) отказов ДУ типа ложная «1».

П римеры возможных схем восстанавливающих органов при r = 3, т.е. .

1. ВО (рис. 4.2). 2. ВО (рис. 4.3)

Рис. 4.3

Рис. 4.2

ВО не корректирует отказы по «1». ВО не корректирует отказы по «0»

3. ВО – возможны два варианта схем (рис. 4.4, 4.5)

Рис. 4.4

Рис. 4.5

(ρ – 1) = 1 отказов по «1»,

ВО корректирует:

(r – ρ) = 1 отказов по «0».

Если используются r однотипных ДУ и ВО типа , то вероятность отказа по «0» такой резервированной структуры (за N = 1 переключение) определяется по формуле:

, (4.2)

где – вероятность отказа по «0» одного ДУ;

– вероятность отказа по «0» i ДУ;

– вероятность неотказа по «0» одного ДУ;

– число сочетаний из r по i, .

Вероятность отказа по «1» такой структуры будет равна:

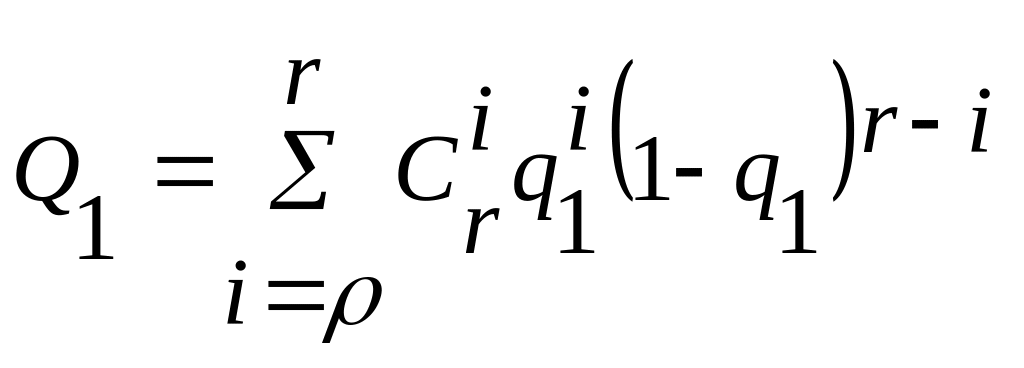, (4.3)

где – вероятность отказа по «1» одного ДУ;

– вероятность неотказа по «1» одного ДУ.

Вероятность безотказной работы избыточной структуры Р и вероятности отказов по «0» Q_о и по «1» Q₁ связаны между собой следующим соотношением:

. (4.4)

Тогда:

. (4.5)

Примечание: В формулах (4.2) (4.5) для простоты принято, что число переключений дискретного устройства равно единице N = 1. Следует помнить, однако, что существует прямая зависимость вероятностей отказов по «1», по «0» и безотказной работы Р от числа переключений N. Поэтому необходимо определять соответствующие вероятности q_o(N); q₁(N); Q_o(N); Q₁(N); P(N) как функции аргумента N при N  1.