1. Точка а1 находится в середине трубки.

Тогда

2. Точка А₁ – в левом торце трубки.

В этом случае

Если

2. Точка а1 находится в правом торце трубки

при

ОТВЕТ: ; при ; при ; при .

ЗАДАЧА 3. По сплошному бесконечному цилиндрическому провод­нику радиусом R течет ток плотности . Рассчитать магнит­ное поле внутри проводника.

ДАНО: R

B – ?

АНАЛИЗ. Проводник нелинейный, поэтому закон Био-Савара-Лапласа применять нельзя. Воспользуемся законом полного тока. Рассчитаем поле в точке А (рис. 2.5.3), находящейся на расстоянии r от цент­ра проводника. Проведем окружность радиусом r с центром в точке О на оси проводника. В силу симметрии модуль вектора в каждой точке окружнос­ти одинаков. Ток, охватываемый этой окружностью, равен

Рис. 2.5.3

Рис. 2.5.4

По закону полного тока (теореме о циркуляции вектора ) для вакуума

.

РЕШЕНИЕ. Проинтегрировав и подставив выражение для тока имеем: Отсюда – индукция поля внутри цилиндрического проводника с током прямо пропорциональна расстоянию от оси проводника. График зависимости В(r) представлен на рис. 2.5.4.

Проверим размерность:

ОТВЕТ: .

ЗАДАЧА 4. Замкнутый тороид имеет N = 400 витков из тонкого провода, намотанных в один слой. Средний диаметр тороида d = 25 см. Определить напряженность и индукцию магнитного поля внутри тороида, ес­ли сила тока I = 0,5 А.

ДАНО: N = 400 d = 0,25 м I = 0,5 А

B – ? H – ?

АНАЛИЗ. Для определения напряженности магнитного поля тороида воспользуемся законом полного тока (теоремой о циркуляции), так как проводники, создающие поле (тороид), обладают симметрией.

РЕШЕНИЕ. Применяя теорему о цирку­ляции вектора вдоль окружнос­ти диаметром d, имеем

причём H = const, H_ = H, поэтому

Правильность формулы по размерности очевидна. Подставив значения, получаем: .

Индукция

ОТВЕТ: ;

ЗАДАЧА 5. При каком соотношении между длиной и диамет­ром d соленоида поле в центре его можно рассчитывать по фор­муле бесконечно длинного соленоида, чтобы ошибка расчета не пре­вышала 1 % ?

ДАНО: %

– ?

АНАЛИЗ. Для решения задачи воспользуемся известными формулами для магнитного поля бесконечного соленоида и соленоида конечных размеров и на их основе выведем необходимое соотношение.

РЕШЕНИЕ. Индукция в центре бесконечно длинного соленоида в вакууме

в центре конечного соленоида

если Тогда

По условию задачи

Поэтому .

Отсюда

Правильность формулы по размерности очевидна.

ОТВЕТ:

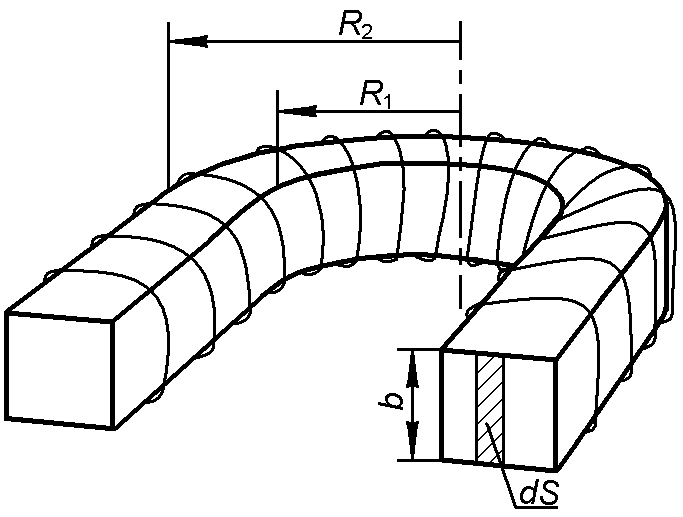
ЗАДАЧА 6. На соленоид с полым картонным сердечником в виде тора с прямоугольным попереч­ным сечением, размеры которо­го показаны на рис.2.5.5, навита обмотка из N = 500 витков, по которой течет ток 2,4 А. Определить максимальное и минимальное значения индукции магнитного поля внутри тороида и магнитный поток системы.

ДАНО: b = 0,05 м R1 = 0,05 м R2 = 0,08 м N = 500 I = 2,4 А

Bmax – ? Bmin – ? Ф – ?

АНАЛИЗ. Линии индукции внут­ри тороида представляют собой окружности, концентричные тороиду.

Благодаря этому индукцию можно найти с помощью закона полного тока для вакуума

Для нахождения магнитного потока площадь поперечного сечения тороида надо разбить на узкие элементарные площадки длиной b и толщиной dr, в пределах которых поле можно считать однородным.

Тогда поток dФ через площадку dS = bdr определится выраже­нием

(2.5.5)

РЕШЕНИЕ. Проведём контур интегрирования в виде окружности радиусом r, с центром на оси тороида. Направление обхода контура выбе­рем так, чтобы во всех точках контура угол между векторами и тождественно был равен нулю и

Абсолютное значение вектора во всех точках контура будет постоянным

Сумма токов, сцепленных с контуром , равна произведению силы тока в обмотке на число витков N, т. е.

Тогда закон полного тока для поля данного тора примет вид: т. е.

Правильность формулы по размерности очевидна.

Поле внутри тороида неоднородно, наибольшего значения индукдия В достигает при r = R₁, наименьшего – при r = R₂ .

Таким образом,

Вектор направлен по нормали к площадке dS и

Полный магнитный поток системы найдем, интегрируя (2.5.5).

Из (2.5.5) получаем:

Проверим размерность: .

Подставив значения, получаем:

ОТВЕТ: ;

ЗАДАЧА 7. Провод в виде тонкого полукольца радиусом R = 10 см находится в однородном магнитном поле с индукцией В = 50мТл. По проводу течет ток I = 10 А. Найти силу F, дей­ствующую на провод, если плоскость полукольца перпендикулярна ли­ниям магнитной индукции, а подводящие провода находятся вне поля.

ДАНО: R = 0,1 м B = 5010–3 Тл I = 10 А

F – ?

АНАЛИЗ. Задача на закон Ампера. Провод нелинейный, поэтому пользоваться выражением для силы Ампера нельзя.

Расположим провод в плоскости чертежа перпендику­лярно линиям магнитной индукции (рис. 2.5.6) и выделим на нем малый элемент с током. Вектор направлен перпендикуляр­но плоскости чертежа (за чертеж). На элемент действует сила Ампера

Сложив элементарные векторы (проинтегрировав), найдем результирующую силу, действующую на полукольцо.

Рис. 2.5.6

РЕШЕНИЕ. Согласно правилу векторного произведения, вектор направ­лен перпендикулярно к и и лежит в плоскости черте­жа. Разложим этот вектор на две составляющие:

(2.5.6)

где – орты координатных осей X, Y; – проекции силы на эти оси, – угол между направлением силы и осью Y.

Модуль вектора равен

т. к.

Силу, действующую на весь проводник, найдём, интегрируя выражение (2.5.6)

где – длина проводника.

Составляющие сил, действующих на обе половинки проводника по оси Х, равны по величине и противоположны по направлению, поэтому

Выразим элемент дуги через приращение угла на этом элементе .

Тогда сила .

Угол меняется от (см. рис. 2.5.6), поэтому

.

Правильность формулы по размерности очевидна.

Подставив значения, получаем:

ОТВЕТ:

ЗАДАЧА 8. В одной плоскости с бесконечно длинным прямым током I = 5 А расположена прямоугольная рамка, обтекаемая током i = 1 А. Найти силы, действующие на каждую сторону рамки со стороны поля, создаваемого прямым током, если длинная сторона b = 20 см параллельна прямому току и находится на расстоянии x₀ = 5 см от него, а короткая сторона a = 10 см (рис.2.5.7).

ДАНО: I = 5 A i = 1 A b = 0,20 м x0 = 0,05 м а = 0,10 м

F1; F2; F3; F4 – ?

АНАЛИЗ. Задача на закон Ампера. Магнитное поле, создаваемое прямым бесконечно длинным проводником с током, действует на все элементы рамки с током по- разному.

Все элементы стороны bc рамки находятся от проводника на одинаковом расстоянии х₀, поэтому в пределах этой стороны магнитное поле проводника одинаково и для определения силы Ампера можно воспользоваться фомулой , где – длина стороны bc; , т. к. проводник лежит в плоскости, перпендикулярной . Аналогично, для стороны . Направления сил и определяются по правилу левой руки и показаны на рис. 2.5.7, причем

Рис. 2.5.7

Вдоль сторон рамки cd (2) и bf (4) индукция поля непрерывно меняется. Выделим элемент проводника dx стороны сd, находящийся на расстоянии x от прямого тока (рис. 2.5.7). Сила, действующая на этот элемент, равна

Направление силы определяется векторным произведением , т. е. сила направлена вверх. Модуль ее по закону Ампера равен

(2.5.7)

т. к. .

Сила , действующая на сторону рамки cd, определяется интегралом

При переходе от одного элемента стороны cd к другому направление элементарных сил не меняется, поэтому можно перейти к скалярной форме записи . (2.5.8)

РЕШЕНИЕ. Бесконечно длинный прямой ток I создает в вакууме магнитное поле, индукция которого

(2.5.9)

где х – расстояние от прямого тока до точки, в которой рассматривается поле.

Для определения сил и подставим (2.5.9) в закон Ампера, имеем и .

Проверим размерность: .

Подставив значения, получаем: ,

Для определения сил и подставим в (2.5.8) выражения (2.5.9) и (2.5.7):

.

Проверим размерность: . Подставив значения, получаем: Н.

Сила , действующая на сторону bf равна по модулю и направлена противоположно ей.

ОТВЕТ: ; Н; ; Н.

ЗАДАЧА 9. Электрон движется в магнитном поле, индукция которого , по винтовой линии с радиусом R = 2 см и шагом «винта» h = 5 см. Определить энергию электрона в электрон-вольтах и направление вектора скорости в начальный момент времени.

ДАНО: В = 510-3 Тл R = 0,02 м h = 0,05 м

WK – ? – ?

АНАЛИЗ. На электрон, влетающий в магнитное поле индукции , действует сила Лоренца

(2.5.10)

Рис. 2.5.8

Направление этой силы в пространстве может меняться по мере изменения направления вектора , вызванного действием этой силы, но она все время остается перпендикулярной к вектору скорости. Таким образом, под действием силы Лоренца движущийся электрон может приобретать только нормальное ускорение. Если бы электрон влетел в магнитное поле перпендикулярно линиям индукции, то он двигался бы по дуге окружности в плоскости, перпендикулярной к линиям индукции. Движение по спирали возможно, если существует составляющая скорости , направленная вдоль поля, не изменяющаяся ни по величине, ни по направлению. Вектор начальной скорости можно представить как, векторную сумму скоростей и , где – составляющая, перпендикулярная вектору индукции; – составляющая, параллельная вектору индукции (рис. 2.5.8).

Записав уравнение динамики для электрона, находим модуль скорости, а, следовательно, и кинетическую энергию электрона.

РЕШЕНИЕ. Под действием силы Лоренца электрон приобретает только нормальное ускорение и по закону Ньютона

где m – масса электрона, и R – радиус винтовой линии, т. е.

Из (2.5.10) следует, что т. к. . Тогда и

. (2.5.11)

Шаг «винта» определится соотношением где Т – период обращения электрона по окружности, равный

Следовательно, продольная составляющая скорости (2.5.12)

Модуль скорости

учитывая (2.5.11) и (2.5.12), имеем

Модуль скорости: .

Кинетическая энергия электрона .

Проверим размерность:

Подставив значения, получаем:

Угол определим из соотношений

или

отсюда .

ОТВЕТ: ; .

ЗАДАЧА 10. Квадратная рамка со стороной а = 2 см, содержащая п = 100 витков тонкого провода, подвешена на упругой нити, постоянная кручения которой С = 10 мкН^.м/град. Плоскость рамки совпадает с направлением линии индукции внешнего магнитного поля. Определить индукцию внешнего магнитного поля, если при пропускании по рамке тока I = 1 А она повернулась на угол = 60.

ДАНО: а = 0,02 м п = 100 C = 10-5 Нм/град I = 1 А = 60

B – ?

АНАЛИЗ. Задача на динамику вращательного движения в магнитном поле. Рамка находится в равновесии, поэтому сумма моментов сил, действующих на нее, равна нулю

. (2.5.13)

На рамку действуют:

Рис. 2.5.9

– момент сил магнитного поля с индукцией :

(2.5.14)

где – магнитный момент рамки; – угол между векторами и ;

• момент упругих сил, возникающих при закручивании нити, на которой подвешена рамка, на угол ,

Подставив и в выражение (2.5.13), получаем уравнение относительно .

РЕШЕНИЕ. Из свойства векторного произведения (формула (2.5.14)) следует, что момент направлен по оси рамки вниз, а из условия (2.5.13) вытекает, что направлен противоположно . Поэтому

Из рис. 2.5.9 видно, что , следовательно, .

Тогда имеем

Проверим разменость: .

Подставляя численные значения, следует иметь в виду, что постоянная кручения С выражена не в радианах, а в градусах, поэтому также необходимо подставить в градусах. Получаем

ОТВЕТ: