1.1.4. Задачи для самостоятельного решения

1. Определить модуль скорости материальной точки в момент времени с, если точка движется по закону , где м/с²; м.

2. Материальная точка движется по закону , где м; м. Определить вектор скорости, вектор ускорения и траекторию движения материальной точки.

3. Радиус-вектор частицы меняется со временем по закону , где (м/с) – постоянный вектор; (с^–1) – постоянная величина. Найти: а) скорость и ускорение частицы в зависимости от времени; б) промежуток времени , по истечении которого частица вернется в исходную точку, а также путь s, который она пройдет при этом.

4. Радиус-вектор частицы изменяется со временем по закону: (м). Найти: а) скорость и ускорение частицы; б) модуль скорости в момент с; в) приближенное значение пути s, пройденного частицей за 11-ю секунду движения.

5. Частица движется со скоростью . Здесь м/с². Найти: а) модуль скорости частицы в момент времени с; б) ускорение частицы и его модуль; в) путь s, пройденный частицей с момента с до момента с.

6. Ускорение материальной точки изменяется по закону , где м/с⁴; м/с². На каком расстоянии от начала координат она будет находиться в момент времени с, если , при ?

7. Электрон движется в некоторой системе отсчета из начального положения, определяемого радиус-вектором где м, м, с начальной скоростью , где м/с и ускорением , где м/с³, м/c². Найти: а) положение электрона в момент времени с; б) скорость электрона при с; в) угол между радиус-вектором и вектором скорости при .

8. Частица движется с ускорением (м/с²). Определить модуль скорости частицы в момент c, если в начальный момент времени скорость была (м/с).

9. Два пловца должны попасть из точки А на одном берегу реки в прямо противоположную точку В на другом берегу. Для этого один из них решил переплыть реку по прямой АВ, другой – все время держать курс перпендикулярно течению, а расстояние, на которое его снесет, пройти по берегу реки со скоростью u. При каком значении u оба пловца достигнут точки В за одинаковое время, если скорость течения км/ч, а скорость каждого пловца относительно воды км/ч?

10. От бакена, который находится на середине широкой реки, отошли две лодки А и В. Обе лодки стали двигаться по взаимно перпендикулярным прямым: лодка А – вдоль реки, а лодка В – поперек. Удалившись на одинаковое расстояние от бакена, лодки вернулись затем обратно. Найти отношение времен движения лодок , если скорость каждой лодки относительно воды в раза больше скорости течения.

11. Лодка движется относительно воды со скоростью в n = 2 раза меньшей скорости течения реки. Под каким углом к направлению течения лодка должна держать курс, чтобы ее снесло течением как можно меньше?

12. Два частицы 1 и 2 движутся с постоянными скоростями и по двум взаимно перпендикулярным прямым к точке их пересечения O. В момент частицы находились на расстояниях ₁ и ₂ от точки О. Через сколько времени после этого расстояние между частицами станет наименьшим? Чему оно равно?

1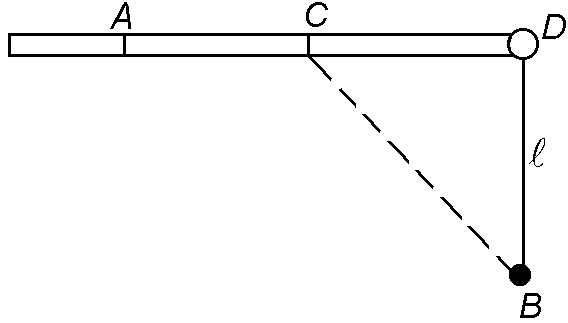 3. Из пункта А, находящегося на шоссе (рис. 1.1.22), необходимо за кратчайшее время попасть на машине в пункт В, расположенный на поле на расстоянии от шоссе. Известно, что скорость машины на поле в  раз меньше ее скорости по шоссе. На каком расстоянии от точки D следует свернуть с шоссе?

14. Лодка пересекает реку с постоянной относительно воды, перпендикулярной к берегам скоростью м/с. Ширина реки м. Скорость течения изменяется по параболическому закону , где y – расстояние от берега, м/с – константа. Найти снос s лодки вниз по течению от пункта ее отправления до места причала на противоположном берегу реки.

15. Частица движется в положительном направлении оси x так, что ее скорость меняется по закону , где – положительная постоянная. В момент времени частица находилась в точке . Найти зависимость от времени скорости и ускорения частицы.

16. Точка движется, замедляясь, по прямой с ускорением, модуль которого зависит от ее скорости по закону , где – положительная постоянная. В начальный момент скорость точки равна . Какой путь она пройдет до остановки? За какое время этот путь будет пройден?

17. Частица движется в плоскости ХY с постоянным ускорением , направление которого противоположно положительному направлению оси Y. Уравнение траектории частицы имеет вид , где и – положительные постоянные. Найти скорость частицы в начале координат.

18. Тело бросили с поверхности Земли под углом к горизонту с начальной скоростью . Пренебрегая сопротивлением воздуха, найти: а) время движения; б) максимальную высоту подъема и горизонтальную дальность полета; при каком значении угла они будут равны друг другу? в) уравнение траектории Y(Х), где Y и Х – перемещение тела по вертикали и горизонтали соответственно.

19. Под каким углом к горизонту надо бросить шарик, чтобы: а) радиус кривизны в начале его траектории был в  = 8,0 раз больше, чем в вершине;

б) центр кривизны вершины траектории находился на земной поверхности?

20. Из пушки выпустили последовательно два снаряда со скоростью м/с: первый под углом  к горизонту, второй – под углом  (азимут один и тот же). Найти интервал времени между снарядами, при котором снаряды столкнутся друг с другом.

21. Воздушный шар начинает подниматься с поверхности земли. Скорость его подъема постоянна и равна . Благодаря ветру шар приобретает горизонтальную компоненту скорости , где – постоянная, y – высота подъема. Найти зависимости от высоты подъема: а) величины сноса шара ; б) полного, тангенциального и нормального ускорений шара.

22. Автомобиль движется по закруглению шоссе, имеющему радиус кривизны 50 м. Уравнение движения автомобиля (м). Найти скорость автомобиля, а также его тангенциальное, нормальное и полное ускорение в момент времени с.

23. Человек, находящийся в комнате на пятом этаже видит, как мимо его окна пролетает сверху предмет. Расстояние 2 м, равное высоте окна, предмет пролетает за 0,1 с. Высота одного этажа 4 м. Определить, с какого этажа упал предмет.

24. Пистолетная пуля пробила два вертикально закрепленных листа бумаги, расстояние между которыми 30 м. Пробоина во втором листе оказалась на 10 см ниже, чем в первом. Определить скорость пули, если к первому листу она подлетела, двигаясь горизонтально.

25. Мяч, брошенный горизонтально, ударяется о стенку, находящуюся на расстоянии 5 м от места бросания. Высота места удара мяча о стенку на 1 м меньше высоты, с которой был брошен мяч. С какой скоростью был брошен мяч? Под каким углом он подлетел к поверхности стенки?

26. Два тела брошены одновременно из одной точки: одно – вертикально вверх, другое – под углом  к горизонту. Начальная скорость каждого тела 25 м/с. Пренебрегая сопротивлением воздуха, найти расстояние между телами через 1,7 с.

27. С какой наибольшей скоростью должен идти под дождем человек, чтобы дождь не капал на ноги, если он держит зонт на высоте 2 м и край зонта выступает вперед на 0,3 м? Капли дождя падают вертикально со скоростью 8м/с.

28. Две подводные лодки плывут навстречу друг другу каждая со скоростью . С первой лодки был послан ультразвуковой сигнал, который отразившись от второй лодки, вернулся обратно через время t. Скорость сигнала . На каком расстоянии находились лодки в момент, когда был послан сигнал?

29. В момент выстрела мишень падает с некоторой высоты. Под каким углом должно быть направлено ружье, чтобы пуля попала в мишень во время ее свободного падения?

30. Колесо вращается с постоянной скоростью, соответствующей 100об/мин. С некоторого момента колесо тормозится и вращается равнозамедленно с угловым ускорением 3 рад/с². Через какое время колесо остановится?

31. Снаряд вылетел со скоростью 320 м/с, сделав внутри ствола 2 оборота. Длина ствола 2 м. Считая движение снаряда в стволе равноускоренным, найти его угловую скорость вращения вокруг оси в момент вылета.

32. На цилиндр, который может вращаться около горизонтальной оси, намотана нить. К концу нити привязали груз и предоставили ему возможность опускаться. Двигаясь равноускоренно, груз за время t = 3 с опустился на = 1,5 м. Определить угловое ускорение  цилиндра, если его радиус R = 4 см.

33. Винт аэросаней вращается с частотой n = 360 мин^–1. Скорость поступательного движения аэросаней равна 54 км/ч. С какой скоростью u движется один из концов винта, если радиус винта R = 1 м?

34. На токарном станке протачивается вал диаметром d = 60 мм. Продольная подача резца = 0,5 мм за один оборот. Какова скорость резания, если за интервал времени t = 1 мин протачивается участок вала длиной =12см?

35. Тело вращается вокруг неподвижной оси Z так, что угол его поворота меняется в зависимости от времени по закону , где a и b – положительные постоянные. Найти момент времени , через которое тело останавливается, а также число оборотов тела N до остановки.

36. Твердое тело вращается вокруг оси Z. Зависимость угла его поворота от времени t описывается законом , где a и b – положительные постоянные. Найти проекции угловой скорости _z и углового ускорения _z на ось Z. Построить графики зависимостей _z(t) и _z(t). Описать качественно характер движения.

37. Твердое тело вращается с угловой скоростью , где рад/с²; рад/с³; – орты осей Х и Y. Найти модули угловой скорости и углового ускорения в момент с.

38. Точка А находится на ободе колеса радиусом R = 0,5 м, которое катится без скольжения по горизонтальной поверхности со скоростью м/с. Найти модуль и направление ускорения точки А.

Рис. 1.1.23

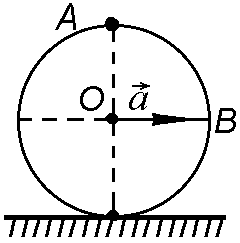
39. Шар радиусом R = 10 см катится без скольжения по горизонтальной плоскости так, что его центр движется с постоянным ускорением см/с². Через t = 2 с после начала движения его положение соответствует рис. 1.1.23. Найти: а) скорости точек А и В в системе отсчета, связанной с Землей; б) ускорения точек А и О.

40. Цилиндр катится без скольжения по горизонтальной плоскости. Радиус цилиндра r. Найти радиусы кривизны траекторий точек А и В (рис. 1.1.23).

Четные номера – Д/З, нечетные - РГР