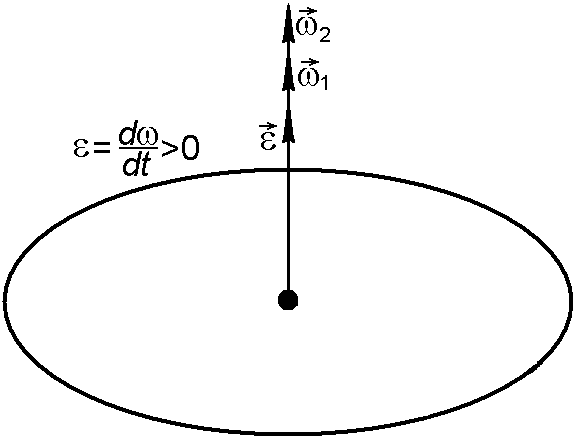25

1. Механика

1.1. Кинематика

1.1.1. Краткие теоретические сведения

1. П оложение материальной точки в пространстве задается

радиус-вектором ,

где – единичные векторы направлений (орты);

x, y, z – координаты точки (рис. 1.1.1).

Абсолютное значение радиус-вектора .

Кинематические уравнения движения :

• (в векторной форме)

• или (в координатной форме) , где t – время.

Уравнение траектории может быть получено из кинематических уравнений координат исключением времени.

2. Скорость:

• Средняя скорость , где – перемещение материальной точки за время t.

• Средняя скалярная (путевая) скорость: , где – путь, пройденный точкой за время .

• Мгновенная скорость, ,

где – проекции скорости на оси координат.

Абсолютное значение скорости .

3. Ускорение

   • Ускорение ,

где – проекции ускорения на оси координат.

• Абсолютное значение ускорения .

• П ри криволинейном движении ускорение можно представить как сумму нормальной и тангенциальной составляющей

. Абсолютное значение этих ускорений: ,

где R – радиус кривизны в данной точке траектории.

4. Путь где – модуль скорости; и – начальный и конечный моменты времени, соответствующие пройденному пути.

5. Перемещение ,

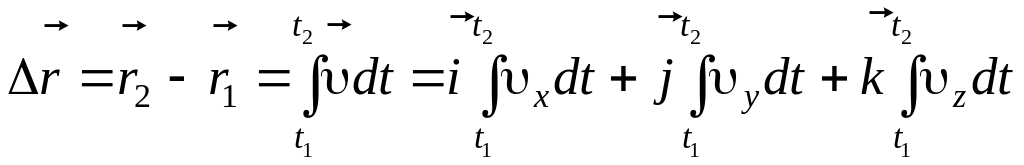где – векторы, соответствующие начальному и конечному положениям материальной точки.

6. Кинематические уравнения равнопеременного движения ( )

,

где – начальная скорость.

7. Положение твердого тела (при заданной оси вращения) определяется углом поворота (или угловым перемещением) . Кинематическое уравнение вращательного движения  = f(t).

8. Средняя угловая скорость <> = /t,

где  – изменение угла поворота за интервал времени t. Мгновенная угловая скорость .

9. Угловое ускорение .

10. Кинематические уравнения равнопеременного вращения ( = const) , где ₀ – начальная угловая скорость.

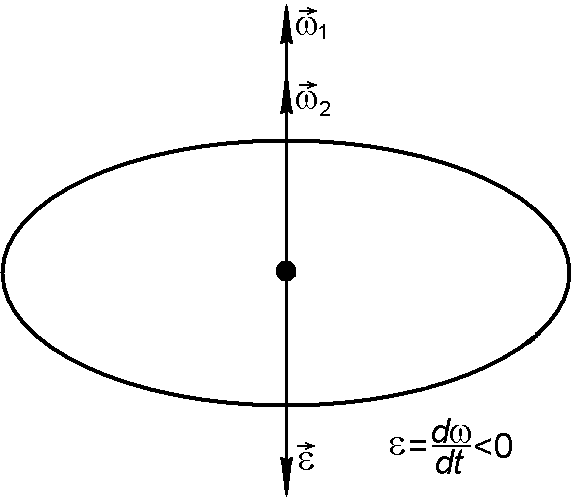
11. Связь между линейными и угловыми величинами, характеризующими вращение материальной точки, выражается следующими формулами (рис. 1.1.3 и 1.1.4):

.

Рис. 1.1.3 Рис. 1.1.4

1.1.2. Методические указания

В кинематике следует различать прямую и обратную задачи. В прямой задаче необходимо получить закон движения, если известны скорость, либо ускорение. В этих случаях используют формулы п. 1.1.1, предварительно проанализировав условие задачи. При анализе необходимо установить начальные условия и записать их в форме дополнительных уравнений. Начальные условия служат для определения констант интегрирования скорости или ускорения.

Систему координат необходимо выбирать в зависимости от условий задачи, чтобы математическое решение было упрощено. Во многих случаях этому требованию удовлетворяет декартова система координат.

Следует обратить внимание на то, что законы движения в координатной форме содержат не путь, проходимый движущимся телом, а только его координаты.

В обратных задачах задается закон движения, из которого скорость и ускорение находятся простым дифференцированием.

Как правило, закон движения удобно записывать либо в координатной форме, либо в векторной как изменение радиус-вектора материальной точки или центра масс системы в зависимости от координат и времени.