
- •Сборник практических занятий по дисциплине «элементы высшей математики»
- •230105 «Программное обеспечение вычислительной техники и автоматизированных систем»
- •П ояснительная записка
- •Практическое занятие №1 Тема: Операции над матрицами. Вычисление определителей
- •Теоретический материал
- •Примеры
- •Задания для самостоятельной работы
- •Практическое занятие №2 Тема: Нахождение обратной матрицы
- •Теоретический материал
- •Задания для самостоятельной работы
- •Практическое занятие №3 Тема: Решение систем алгебраических уравнений по правилу Крамера и матричным методом
- •Задания для самостоятельной работы
- •Практическое занятие №4 Тема: Решение систем алгебраических уравнений методом Гаусса
- •Теоретический материал
- •Задания для самостоятельной работы
- •Практическое занятие №5 Тема: Операции над векторами. Вычисление модуля и скалярного произведения
- •Теоретический материал
- •Задания для самостоятельной работы
- •Практическое занятие №6 Тема: Составление уравнений прямых и кривых второго порядка, их построение
- •Теоретический материал
- •Задания для самостоятельной работы
- •Практическое занятие №7 Тема: Вычисление пределов с помощью замечательных пределов, раскрытие неопределенностей
- •Теоретический материал
- •Задания для самостоятельной работы
- •Практическое занятие №8 Тема: Вычисление односторонних пределов, классификация точек разрыва
- •Теоретический материал
- •Задания для самостоятельной работы
- •Практическое занятие №9 Тема: Вычисление производных функций по определению производной
- •Теоретический материал
- •Задания для самостоятельной работы
- •Практическое занятие №11 Тема: Вычисление производных и дифференциалов высших порядков
- •Теоретический материал
- •Примеры
- •Задания для самостоятельной работы
- •Практическое занятие №12 Тема: Полное исследование функции. Построение графиков
- •Теоретический материал
- •Задания для самостоятельной работы
- •Практическое занятие №13 Тема: Интегрирование заменой переменной и по частям в неопределенном интеграле
- •Теоретический материал
- •Примеры
- •Задания для самостоятельной работы
- •Практическое занятие №14 Тема: Вычисление определенных интегралов
- •Теоретический материал
- •Примеры
- •Задания для самостоятельной работы
- •Практическое занятие №15 Тема: Вычисление площадей фигур с помощью определенных интегралов
- •Теоретический материал
- •Примеры
- •Задания для самостоятельной работы
- •Практическое занятие №16
- •Теоретический материал
- •Примеры
- •Задания для самостоятельной работы
- •Практическое занятие №17
- •Теоретический материал
- •Примеры
- •Задания для самостоятельной работы
- •Практическое занятие №18
- •Теоретический материал
- •Примеры
- •Задания для самостоятельной работы
- •Практическое занятие №19
- •Теоретический материал
- •Примеры
- •Задания для самостоятельной работы
- •Практическое занятие №20
- •Теоретический материал
- •Примеры
- •Задания для самостоятельной работы
- •Практическое занятие №21
- •Теоретический материал
- •Примеры
- •Задания для самостоятельной работы
- •Практическое занятие №22
- •Теоретический материал
- •Примеры
- •Задания для самостоятельной работы
- •Практическое занятие №23
- •Теоретический материал
- •Примеры
- •Задания для самостоятельной работы
- •Практическое занятие №24
- •Теоретический материал
- •Примеры
- •Задания для самостоятельной работы
- •Практическое занятие №25
- •Теоретический материал
- •Примеры
- •2) Здесь , , . Точка, изображающая число , лежит во II четверти; , . Значит,
- •Задания для самостоятельной работы
- •С писок рекомендуемой литературы
Задания для самостоятельной работы
Найти интегралы методом непосредственного интегрирования:
1)
![]() ; 2)
; 2)
![]() ;
;
3)
![]() ; 4)
; 4)
![]() ;
;
5)
![]() ; 6)
; 6)
![]() ;
;
7)
![]() ; 8)
; 8)
![]() ;
;
9)
![]()
Найти интегралы способом подстановки:
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() ;
;
4)
![]() ; 5)
; 5)
![]() ; 6)
; 6)
![]() ; 7)
; 7)
![]() ; 8)
; 8)
![]() ; 9)
; 9)
![]() .
.
Найдите интегралы при помощи интегрирования по частям:
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() ; 4)
; 4)
![]() ; 5)
; 5)
![]() ; 6)
; 6)
![]() .
.
Вопросы для самоконтроля:
Что называется первообразной? Перечислите свойства первообразной функции.
Что называется неопределенным интегралом?
Какие свойства неопределенного интеграла вы знаете?
Перечислите основные формулы интегрирования.
Какие методы интегрирования вы знаете? В чем заключается их сущность?
Практическое занятие №14 Тема: Вычисление определенных интегралов
Цель: Формирование навыков вычисления определенного интеграла при помощи формулы Ньютона – Лейбница
На выполнение работы отводится 2 часа
Требования к выполнению работы:
Ответить на теоретические вопросы.
Оформить задания в тетради для практических работ.
Теоретический материал
Функция,
интегрируемая на промежутке
![]() ,
если при любых разбиениях
,
если при любых разбиениях
![]() промежутка
,
таких, что
промежутка
,
таких, что
![]() при произвольном выборе точек
при произвольном выборе точек
![]() (где
(где
![]() ),
сумма
),
сумма
![]() при
при
![]() стремится к пределу
стремится к пределу
![]() .
.
Предел
![]() называют определенным интегралом
от функции
на промежутке
и обозначают
называют определенным интегралом
от функции
на промежутке
и обозначают
![]() ,
то есть
,
то есть
![]() .
.
Число называется нижним пределом интеграла, - верхним. Промежуток называется промежутком интегрирования, - переменной интегрирования.
Для вычисления
определенного интеграла от функции
в том случае, когда можно найти
соответствующий неопределенный интеграл
![]() ,
служит формула Ньютона – Лейбница:
,
служит формула Ньютона – Лейбница:
![]() .
То есть определенный интеграл равен
разности значений первообразной при
верхнем и нижнем пределах интегрирования.
.
То есть определенный интеграл равен
разности значений первообразной при
верхнем и нижнем пределах интегрирования.
Примеры
Вычислить следующие определенные интегралы:
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() .
.
Решение:
1)
![]() ;
;
2)
![]() ;
;
3)![]()
![]()
![]() .
.
Задания для самостоятельной работы
Вычислить определенные интегралы:
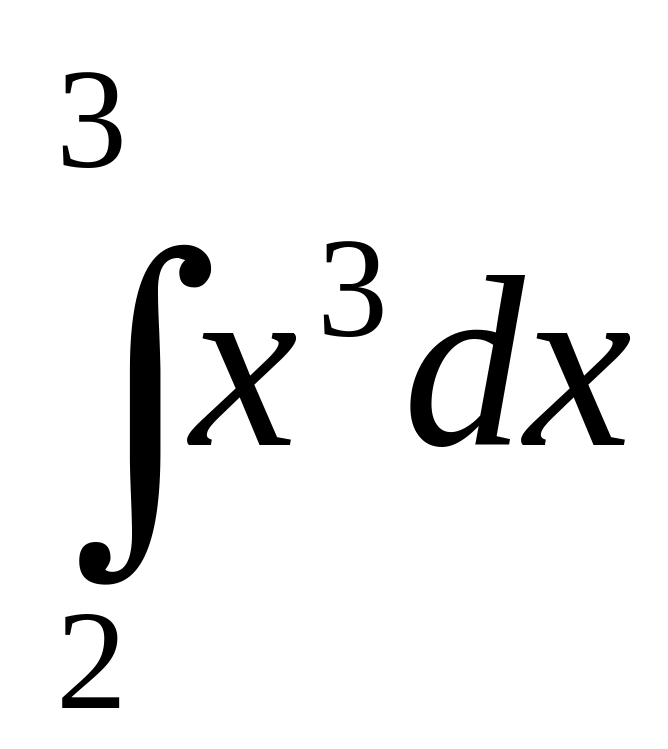 ; 2)
; 2)
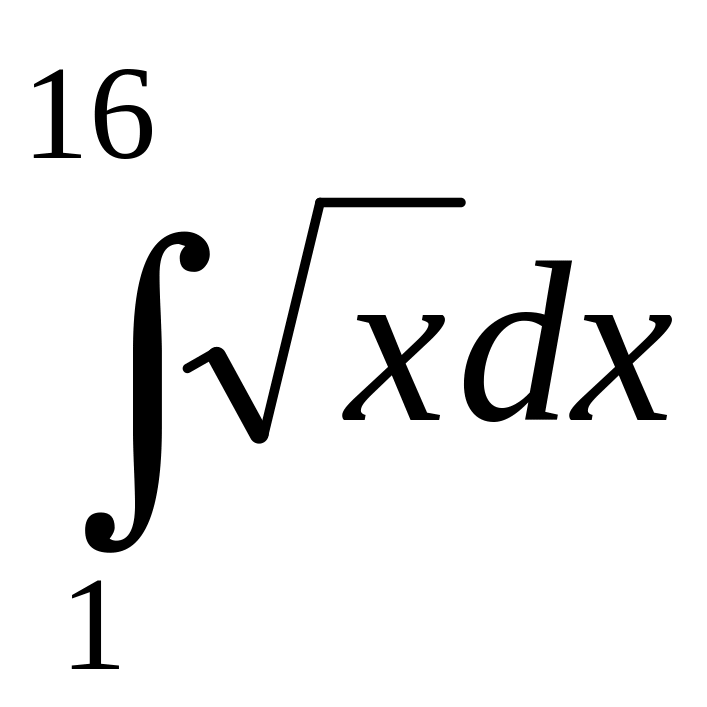 ; 3)
; 3)
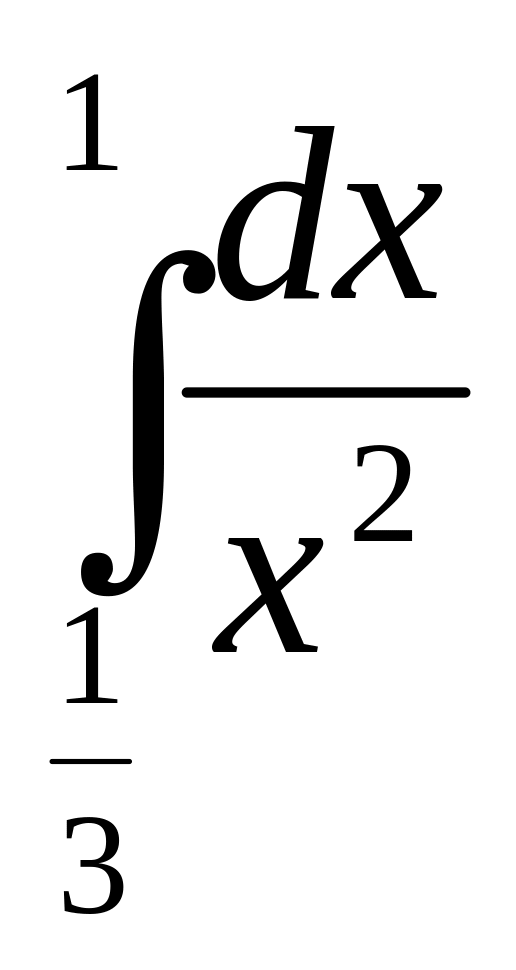 ;
;
4)
![]() ; 5)
; 5)
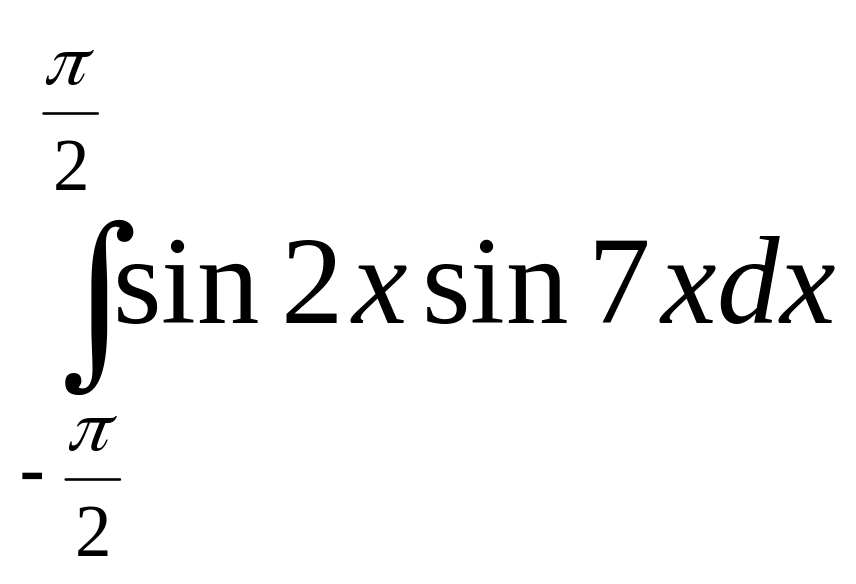 6)
6)
![]() ;
;
7)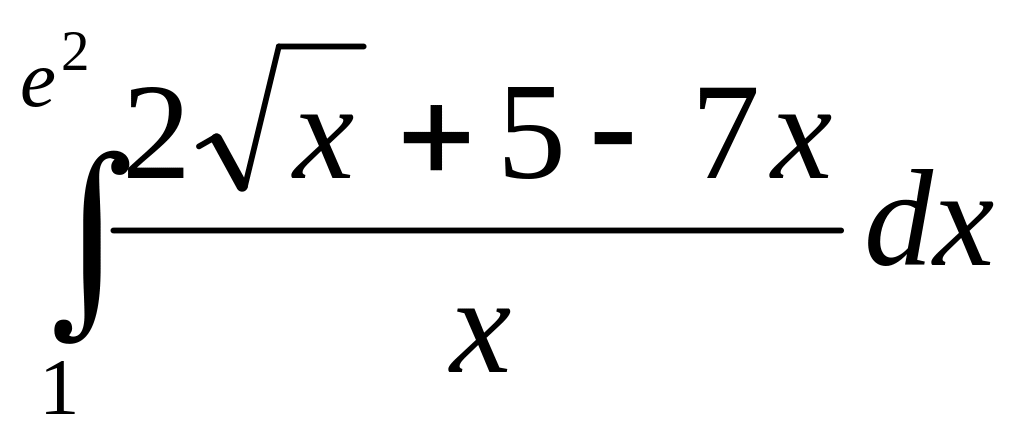 ; 8)
; 8)
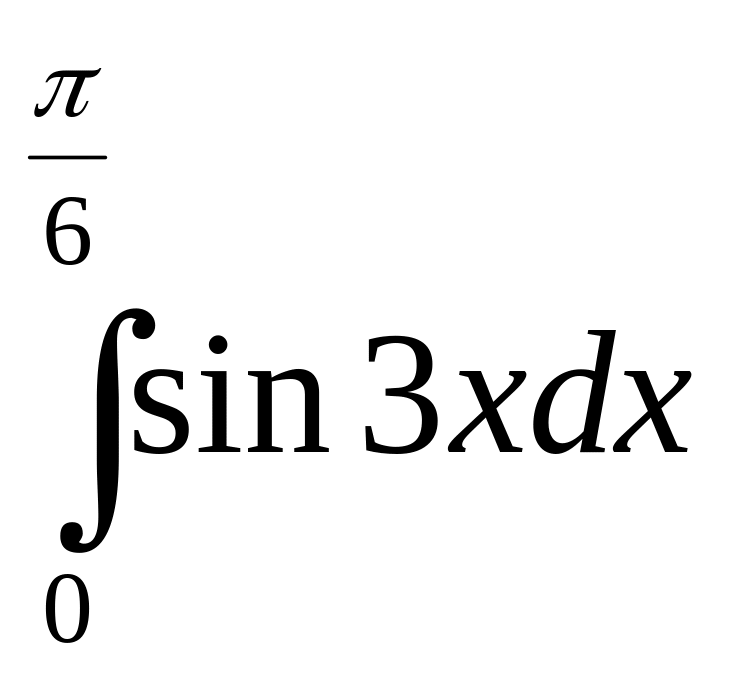 ;
;
9)
![]() ; 10)
; 10)
![]() ; 11)
; 11)
![]() ;
;
12)
![]() ; 13)
; 13)
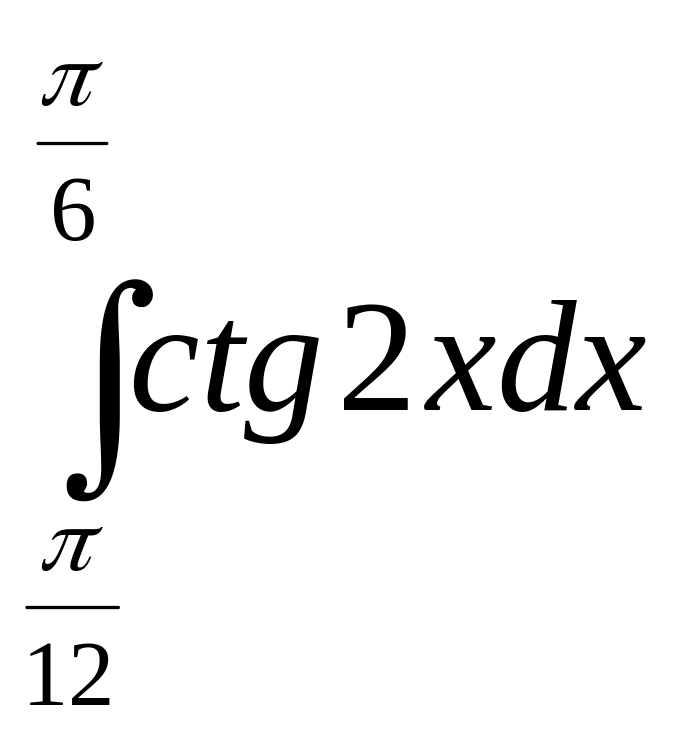 ; 14)
; 14)
 ;
;
Вопросы для самоконтроля:
Что называется интегральной суммой для функции на отрезке?
Дайте определение определенного интеграла.
Сформулируйте основные свойства определенного интеграла.
В чем заключается суть формулы Ньютона – Лейбница?
Практическое занятие №15 Тема: Вычисление площадей фигур с помощью определенных интегралов
Цель: Формирование навыков вычисления площадей фигур с помощью определенных интегралов
На выполнение практической работы отводится 2 часа
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы
2.Оформить задания в тетради для практических работ
Теоретический материал
Определенный интеграл широко применяется при вычислениях различных геометрических фигур и физических величин.
Найдем площадь
криволинейной трапеции, ограниченной
кривой
,
осью
и двумя прямыми
и
![]() ,
где
,
где
![]() ,
,
![]() (рис. 1).
(рис. 1).
Т ак
как дифференциал переменной площади
есть площадь прямоугольника с основанием
и высотой
,
то есть
ак
как дифференциал переменной площади
есть площадь прямоугольника с основанием
и высотой
,
то есть
![]() ,
то, интегрируя это равенство в пределах
от
до
,
получим
,
то, интегрируя это равенство в пределах
от
до
,
получим
![]() .
.
Если
криволинейная трапеция прилегает к оси
так, что
![]() ,
,
![]() (рис. 2), то дифференциал переменной
площади
равен
(рис. 2), то дифференциал переменной
площади
равен
![]() ,
откуда
,
откуда
![]() .
.


В том случае, когда
криволинейная трапеция, ограниченная
кривой
,
осью
и прямыми
и
,
лежит под осью
(рис.3), площадь находится по формуле
![]() .
.
Е
x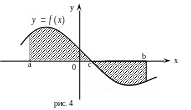 сли
фигура, ограниченная кривой
,
осью
и прямыми
и
,
расположена по обе стороны от оси
сли
фигура, ограниченная кривой
,
осью
и прямыми
и
,
расположена по обе стороны от оси
![]() .
.

Пусть фигура
ограничена двумя пересекающимися
кривыми
![]() и
и
![]() ,
и прямыми
и
,
где
и
,
и прямыми
и
,
где
и
![]() (рис. 5). Тогда ее площадь находится по
формуле
(рис. 5). Тогда ее площадь находится по
формуле
![]() .
.
