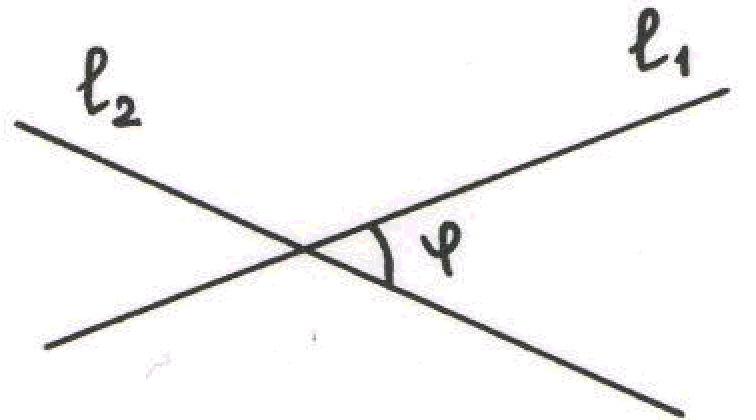
2. Взаимное расположение прямых на плоскости

Две прямые на плоскости могут быть параллельны или пересекаться (под прямым или произвольным углом).

1. Условие параллельности двух прямых

Пусть прямые l₁ и l₂ заданы своими общими уравнениями:

l₁ : A₁x+B₁y+C₁=0

l₂ : A₂x+B₂y+C₂=0

Если прямые l₁ и l₂ параллельны, то их нормальные векторы (A₁, B₁) и (A₂, B₂)

коллинеарны. Используя условие коллинеарности векторов, получаем условие параллельности прямых:

l1  l2  =

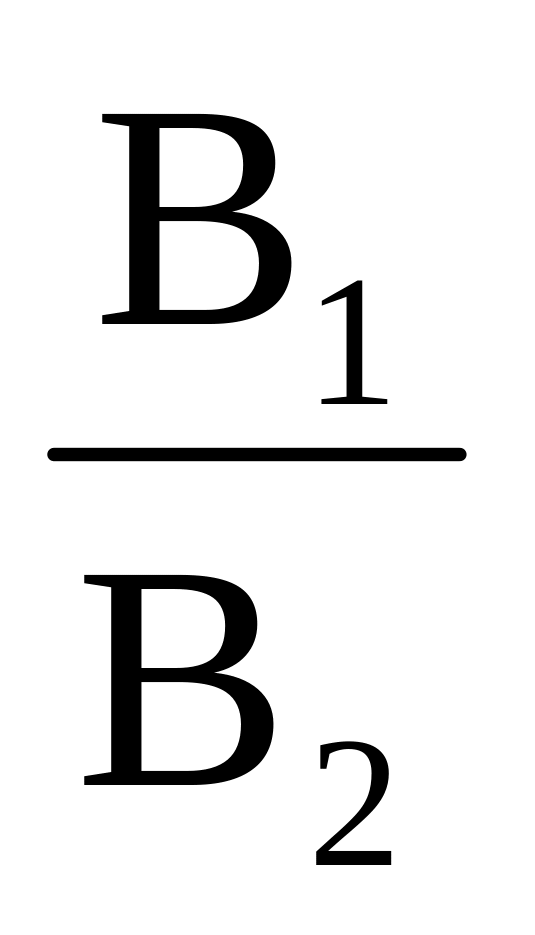
т.е. коэффициенты при соответствующих переменных пропорциональны.

Замечание: Прямые l₁ и l₂ совпадают  = = .

Пусть прямые l₁ и l₂ заданы уравнениями с угловыми коэффициентами:

l₁ : у=k₁x+b₁

l₂ : у=k₂x+b₂

Если прямые l₁ и l₂ параллельны, то они образуют одинаковые углы с осью Ох. В этом случае условие параллельности прямых имеет вид:

l1  l2  k1=k2

т.е. угловые коэффициенты равны.

Замечание: Прямые l₁ и l₂ совпадают  k₁=k₂, b₁=b₂ .

2. Условие перпендикулярности двух прямых

Пусть прямые l₁ и l₂ заданы своими общими уравнениями:

l₁ : A₁x+B₁y+C₁=0

l₂ : A₂x+B₂y+C₂=0

Если прямые l₁ и l₂ перпендикулярны, то их нормальные векторы (A₁, B₁) и (A₂, B₂) ортогональны. Используя условие ортогональности векторов, получаем условие перпендикулярности прямых:

l1  l2  A1A2+B1B2=0

т.е. сумма произведений коэффициентов при соответствующих переменных равна 0.

Пусть прямые l₁ и l₂ заданы уравнениями с угловыми коэффициентами:

l₁ : у=k₁x+b₁

l₂ : у=k₂x+b₂

Если прямые l₁ и l₂ перпендикулярны, то они образуют с осью Ох углы, отличающиеся на 90.

Пусть k1=tg. Тогда k2=tg(+/2). Используем тригонометрические преобразования: tg(+/2)=-ctg=-1/tg Окончательно имеем:

k₂=-1/k₁ или, наоборот, k₁=-1/k₂

Таким образом, условие перпендикулярности двух прямых:

l1  l2  k1=-

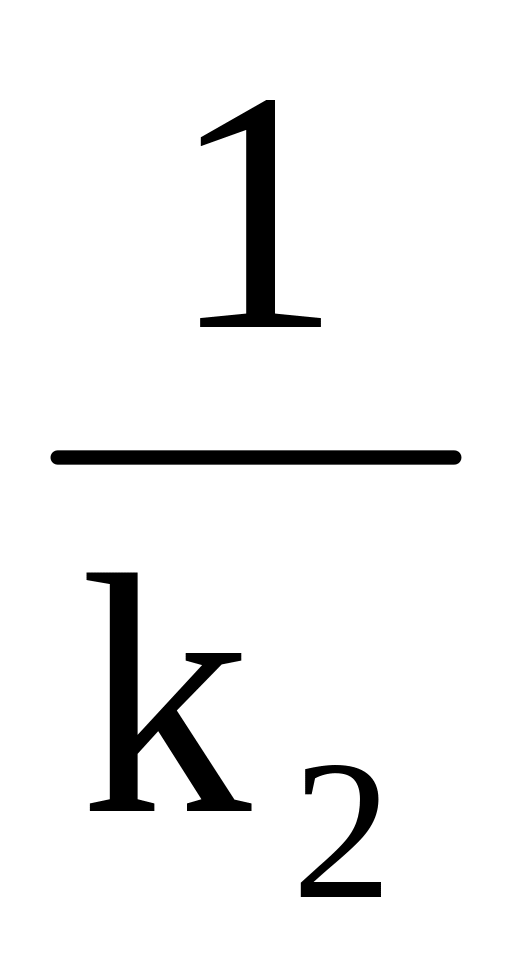
т.е. угловые коэффициенты обратны по величине и противоположны по знаку.

3. Точка пересечения двух прямых

Пусть прямые l₁ и l₂ заданы своими общими уравнениями:

l₁ : A₁x+B₁y+C₁=0

l₂ : A₂x+B₂y+C₂=0

Точка пересечения лежит на обеих прямых. Поэтому ее координаты удовлетворяют одновременно обоим уравнениям. Для определения координат необходимо составить из уравнений прямых систему уравнений и решить ее:

 A1x+B1y+C1=0  A2x+B2y+C2=0

Таким образом, координаты точки пересечения прямых находятся путем совместного решения уравнений этих прямых.

Аналогично, если прямые l₁ и l₂ заданы уравнениями с угловыми коэффициентами:

l₁ : у=k₁x+b₁

l₂ : у=k₂x+b₂

координаты точки их пересечения определяются из системы уравнений:

 у=k1x+b1  у=k2x+b2

4. Угол между двумя прямыми

Пусть прямые l₁ и l₂ заданы своими общими уравнениями:

l1 : A1x+B1y+C1=0 l2 : A2x+B2y+C2=0

Угол между прямыми равен углу между их нормальными векторами (A₁, B₁) и (A₂, B₂):

cos =

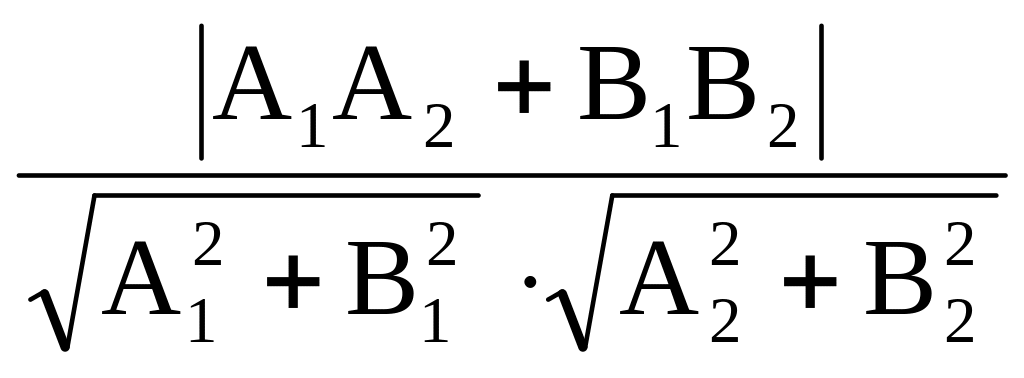
Пусть прямые l₁ и l₂ заданы уравнениями с угловыми коэффициентами:

l₁ : у=k₁x+b₁

_{l2 : у=k2x+b}2

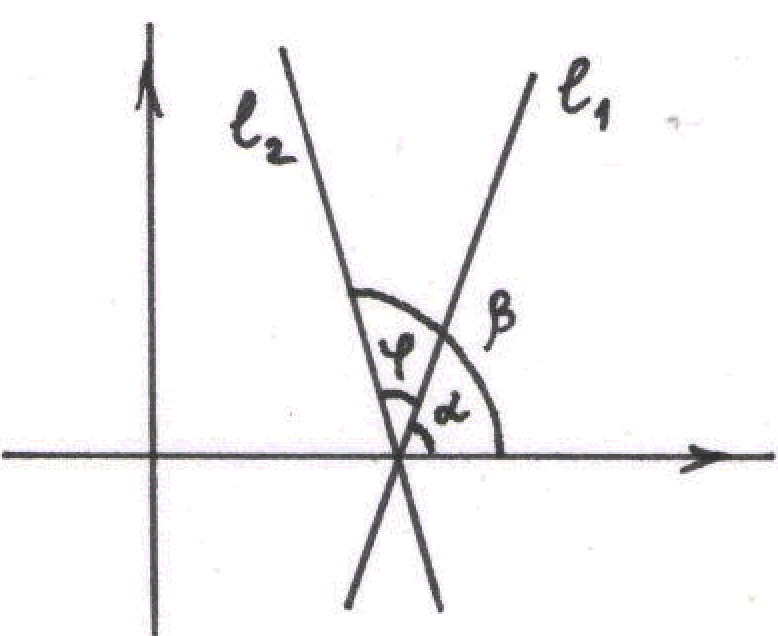
В этом случае угол между прямыми удобно выразить через тригонометрическую функцию тангенс: tg=tg(-)= =

Таким образом,

tg =

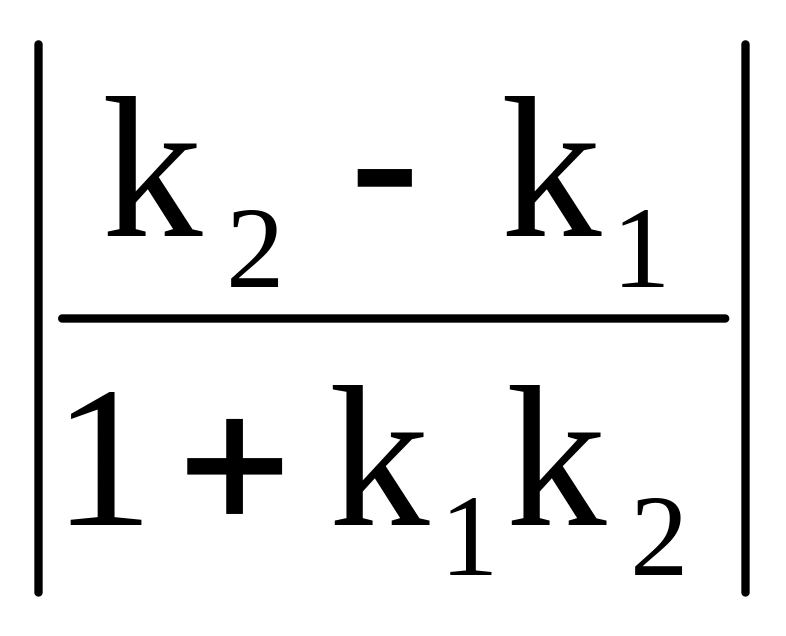
Замечание: Для нахождения острого угла между прямыми выражения в правых частях этих формул взяты по модулю.