1. Уравнения прямой на плоскости

Одну и ту же прямую на плоскости можно описывать различными по виду уравнениями. Ниже представлены возможные виды уравнения прямой на плоскости.

1. Общее уравнение прямой

Уравнение алгебраической линии первой степени относительно х и у, т.е. уравнение вида:

Ax+By+C=0

, A2+B20

определяет на плоскости некоторую прямую. Это уравнение называется общим уравнением прямой.

Частные случаи общего уравнения прямой:

Значение коэффициента	Вид уравнения	Положение прямой
С=0 A=0 В=0 A=С=0 B=С=0	Ax+By=0 By+С=0 Ах+С=0 у=0 х=0	проходит через начало координат параллельна оси Ох параллельна оси Оу совпадает с осью Ох совпадает с осью Оу

2) Векторное уравнение прямой

Составим уравнение прямой, проходящей через заданную точку в направлении, перпендикулярном заданному.

Обозначим прямую – l, заданную точку – М₀(х₀, у₀), направление зада-

дим вектором (A, B). Тогда, по условию: М0(х0, у0)l (A, B)  l

Вектор называется нормалью (нормальным вектором) прямой l.

Рассмотрим на прямой l текущую точку М(х, у).

М(х, у)l     =0

Рассмотрим дополнительно начальную точку О, относительно которой определим радиус-векторы и точек М₀ и М соответственно. Тогда последнее соотношение запишется в виде:

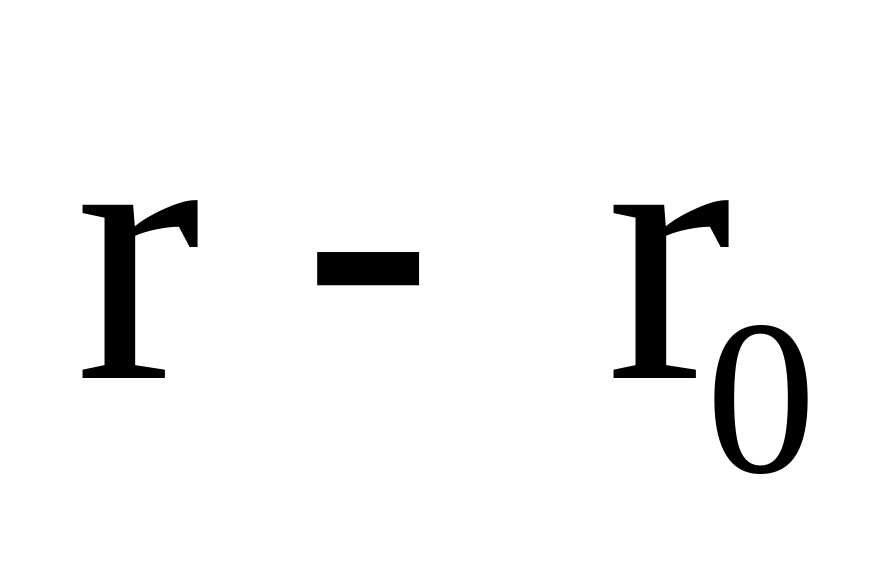( )=0

– векторное уравнение прямой

Если это векторное уравнение переписать в координатной форме, то получится общее уравнение прямой:

A(x-х₀)+B(y-у₀)=0

3) Параметрическое уравнение прямой

Составим уравнение прямой, проходящей через заданную точку в заданном направлении. (Направление задается направляющим вектором).

Обозначим прямую – l, заданную точку – М₀(х₀, у₀), направление зада-

дим вектором (p, q). Тогда, по условию: М0(х0, у0)l (p, q)  l, 

Вектор называется направляющим вектором прямой l.

Рассмотрим на прямой l текущую точку М(х, у).

М(х, у)l    =t , где t – некоторый параметр.

Рассмотрим дополнительно начальную точку О, относительно которой определим радиус-векторы и точек М₀ и М соответственно. Тогда последнее соотношение запишется в виде:

=t или = +t – векторно-параметрическое уравнение прямой

Перепишем его в координатной форме:

 x=x0+tp  y=y0+tq

– параметрическое уравнение прямой

4) Каноническое уравнение прямой

Исключим параметр t в параметрическом уравнении прямой:

 x=x₀+tp  t=

 y=y₀+tq  t=

=	– каноническое уравнение прямой

Замечания: Если р=0, то х=х₀ – каноническое уравнение прямой

Если q=0, то у=у₀ – каноническое уравнение прямой

5) Уравнение прямой с угловым коэффициентом

Если в общем уравнении прямой В0, то, разрешив его относительно у, получим уравнение вида:

y=kx+b

где k=-A/B, b=-C/B. Его называют уравнением с угловым коэффициентом,

поскольку k=tg – угловой коэффициент, равный тангенсу угла наклона прямой к оси Ох. b – ордината точки пересечения прямой с осью Оу.

Частные случаи уравнения прямой с угловым коэффициентом:

Значение коэффициента	Вид уравнения	Положение прямой
b=0 k=0 (=0) k не существует (=/2)	y=kx y=b х=a	проходит через начало координат k>0: k<0: параллельна оси Ох параллельна оси Оу

6) Уравнение прямой, проходящей через заданную точку в заданном направлении. (Направление задается углом наклона прямой к оси Ох.)

Обозначим прямую – l, заданную точку – М₀(х₀, у₀),  – угол наклона

прямой l к оси Ох (/2). Тогда, по условию: М0(х0, у0)l Рассмотрим на прямой l текущую точку М(х, у).

М(х, у)l  у=kx+b, т.е. координаты точки М удовлетворяют уравнению прямой с угловым коэффициентом.

М₀(х₀, у₀)l  у₀=kx₀+b, т.е. координаты точки М₀ удовлетворяют этому же уравнению прямой.

Вычитая одно соотношение из другого и тем самым исключив неизвестный параметр b, получим требуемое уравнение прямой:

y-y0=k(x-x0)

Замечание: Если k – произвольное число, то уравнение определяет пучок прямых, проходящих через точку М0(х0, у0), кроме прямой, параллельной оси Оу и не име-

ющей углового коэффициента. (На рисунке эта прямая изображена пунктиром.)

7) Уравнение прямой, проходящей через две заданные точки

Обозначим прямую – l, заданные точки – М₁(х₁, у₁) и М₂(х₂, у₂).

Тогда, по условию: М1(х1, у1)l, М2(х2, у2)l Используем уравнение прямой, проходящей через заданную точку М1: y-y1=k(x-x1)

М₂(х₂, у₂)l  y₂-y₁=k(x₂-x₁), т.е. координаты точки М₂ удовлетворяют этому же уравнению прямой.

Из последнего соотношения выразим угловой коэффициент:

k=

и подставим его выражение в исходное уравнение:

y-y₁= (x-x₁)

Перепишем уравнение в симметричной форме:

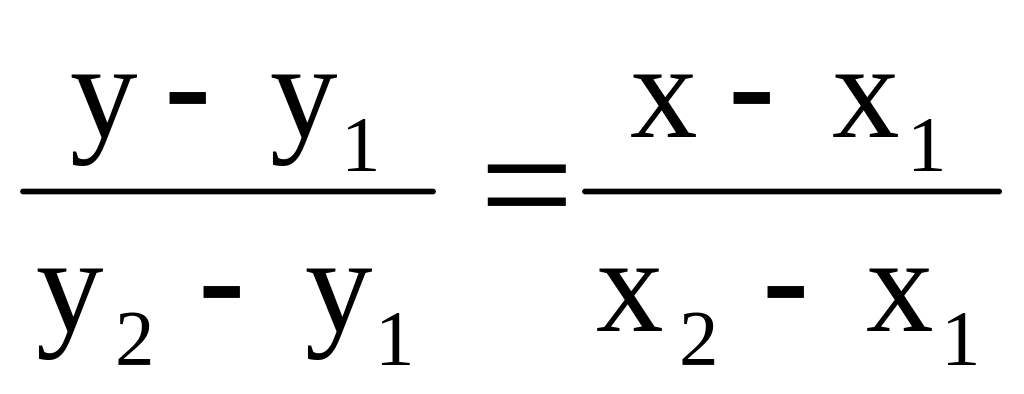
– уравнение прямой, проходящей через две заданные точки

8) Уравнение прямой в отрезках на осях

Составим уравнение прямой по заданным отрезкам а0 и b0, отсекаемым на осях координат.

Фактически известны координаты точек пересечения прямой с осями координат. Используем уравнение прямой, проходящей через точки А(а, 0) и В(0, b):



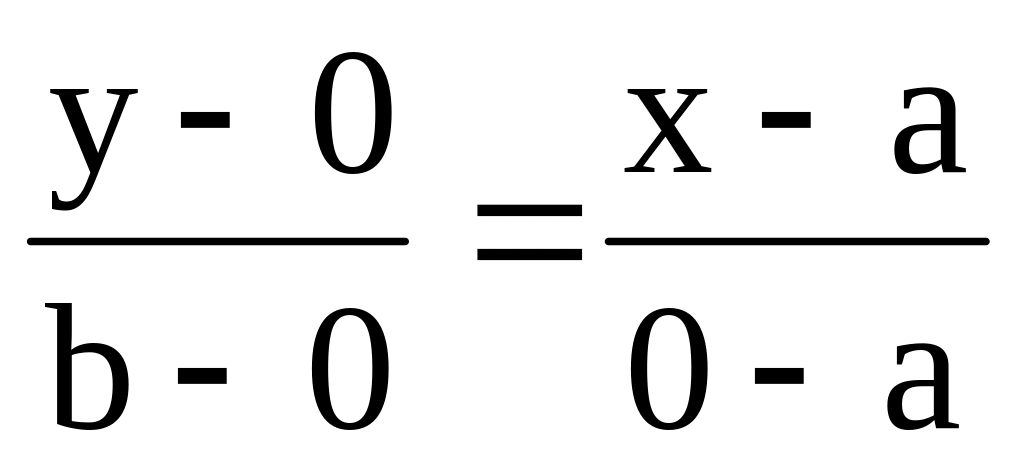
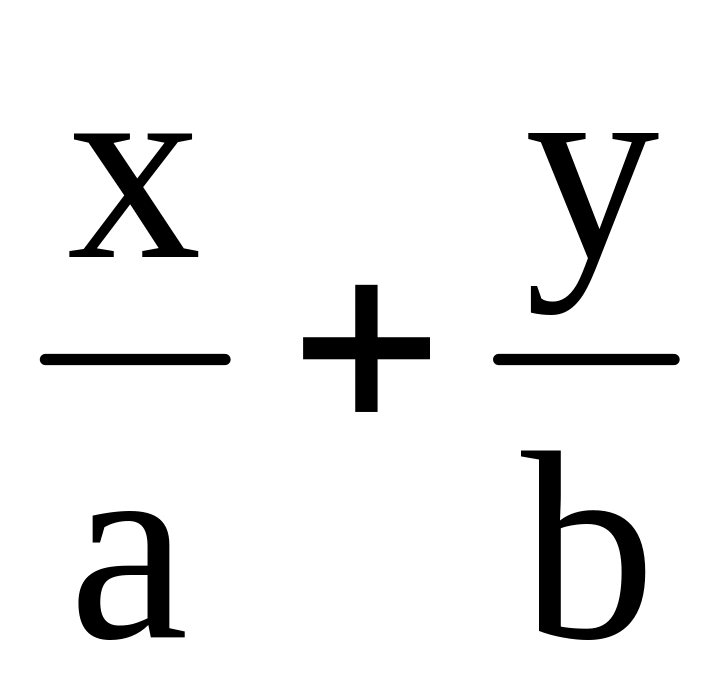=1

– уравнение прямой в отрезках на осях

Замечание: Выбор того или иного вида уравнения прямой на практике производится в зависимости от имеющихся исходных данных. С помощью несложных преобразований всегда можно перейти от одного вида уравнения прямой к другому его виду.